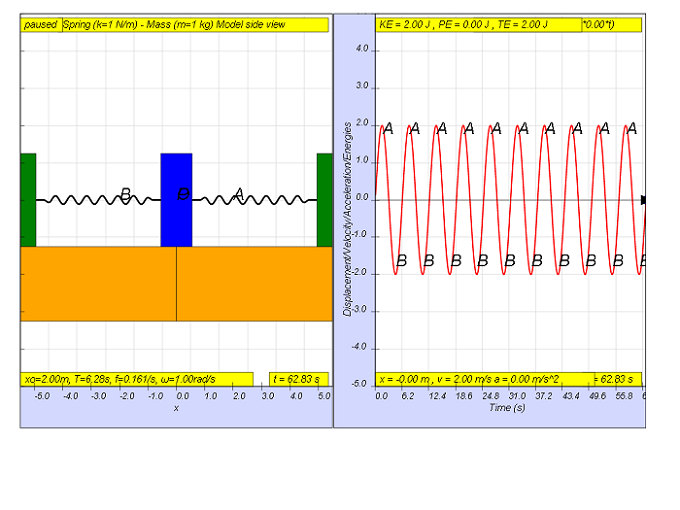
Cuando un sistema realiza oscilaciones sin ninguna fuerza aplicada, la frecuencia de la oscilación es una característica del sistema y es llamada la frecuencia natural, fo . En el ejemplo anterior, fo = 0.161 Hz.

Cuando un sistema realiza oscilaciones sin ninguna fuerza aplicada, la frecuencia de la oscilación es una característica del sistema y es llamada la frecuencia natural, fo
. En el ejemplo anterior, fo
= 0.161 Hz.
Considere un sistema de masa-resorte inicialmente en reposo.
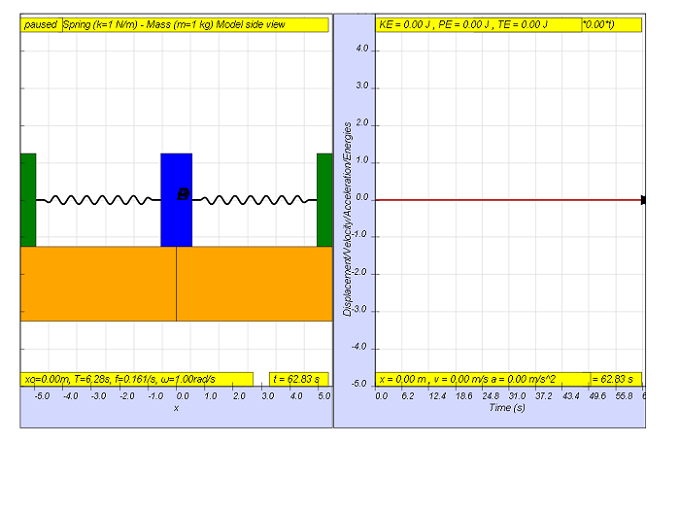
Cuando la fuerza motriz es f = 0, eso significa que la fuerza motriz es Fmotriz = (0.5)sen(2π f t ) = 0.
el resultado es el que se muestra en la imagen donde x = 0 para todos los tiempos, ya que no hay ninguna fuerza de accionamiento externa que actúe sobre el sistema.
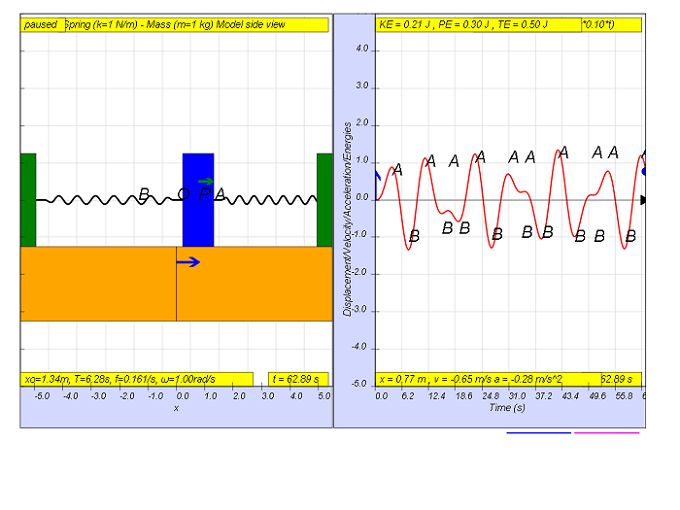
Sin embargo, cuando f = 0.1, el Fmotriz = (0.5)sen(2π(0.1)t), da como resultado un movimiento que parece irregular y alcanza una amplitud máxima de A y B (ver imagen).
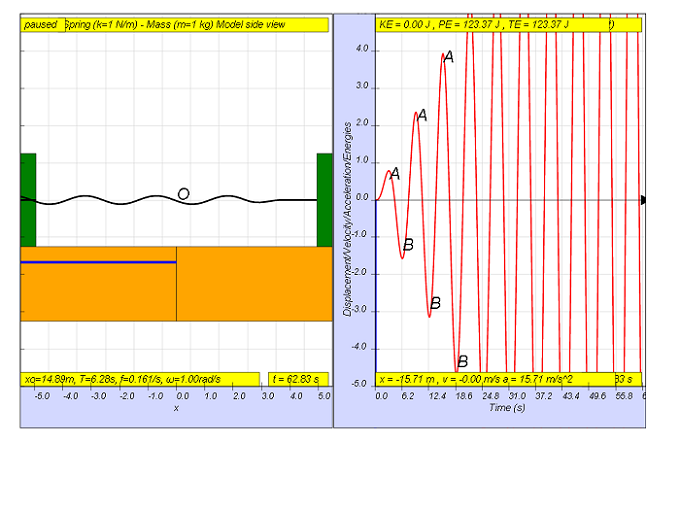
Por otra parte, cuando f = 0.159 , Fmotriz = (0.5)sen(2π(0.159)t), da como resultado un movimiento que parece aumentar hasta una amplitud máxima muy grande de A y B (vea la imagen, cuando t = 55.8, A y B son mayores que la altura de visualización de la pantalla). Teóricamente, debe ser infinitamente grande.
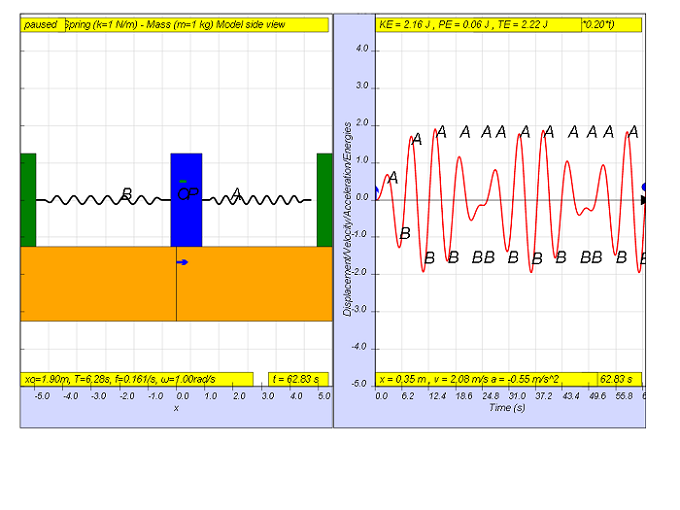
Ahora, cuando f = 0.2 , Fmotriz = (0.5)sen(2π(0.2)t), da como resultado un movimiento que parece alcanzar también una amplitud máxima más pequeña de A y B (ver en la imagen que llega a aproximadamente a 1,8).
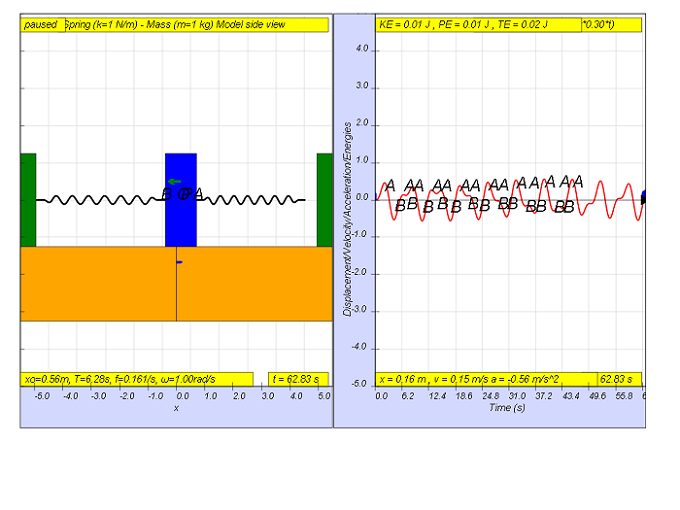
Si f = 0.3, Fmotriz = (0.5)sen(2π(0.3)t), da como resultado un movimiento que parece alcanzar también la amplitud máxima de A y B (ver imagen que llega a aproximadamente 0,5).
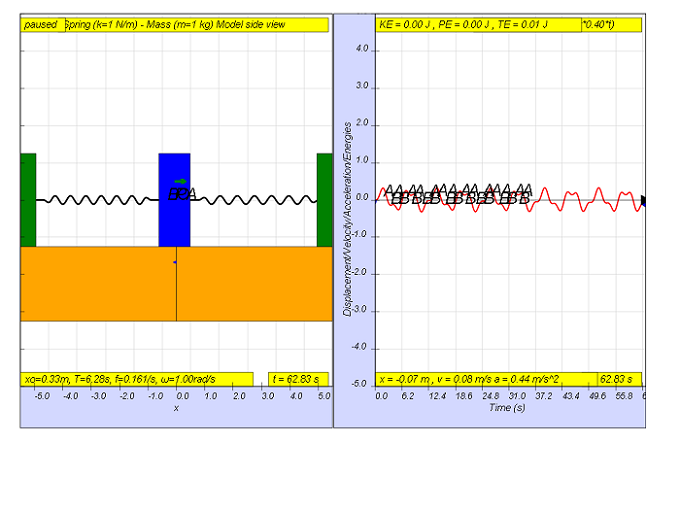
Finalmente, cuando f = 0.4, Fmotriz = (0.5)sen(2π(0.4)t), da como resultado un movimiento que parece alcanzar también una amplitud máxima aún menor de A y B (ver imagen que llega a aproximadamente 0,3).
Estas oscilaciones en las que se impone una fuerza periódica se denominan resonancia forzada. Entonces, algunos sistemas influirán en la vibración a la frecuencia de la fuerza periódica, f, pero únicamente cuando f = fo = 0.161 Hz , en este ejemplo, la amplitud máxima es la máxima que se produce en este caso cuando la amortiguación es cero, ya que tiene efectos de amplitud máxima similares para diferentes niveles de amortiguación que ocurren cerca de f = fo
1) Vibraciones de un reloj de péndulo.
2) Vibraciones de un diapasón cuando se expone a la fuerza periódica de una onda de sonido.
3) Vibración de un puente bajo la influencia de soldados en marcha o Viento periódico.