71. 3.6 m/s
73. bD4/4
75. Normal
77.
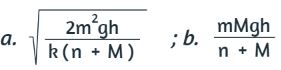
79. a. 2.24 m/s; b. 1.94 m/s; c. 1.94 m/s
81. 18 m/s
83. vA = 24 m/s; vB = 14 m/s; vC = 31 m/s
85. a. Pérdida de energía en 240 N•m; F = 8 N
87 89.7 m/s
89 32 J
8.1 (4.63 J) - (- 2.38 J) = 7.00 J
8.2 35.3 kJ, 143 kJ, 0
8.3 22.8 cm. Utilizando 0.02 m para el desplazamiento inicial del resorte, calculamos que el desplazamiento final del resorte que es de 0.028 m; por lo tanto, la longitud del resorte es la longitud no estirada más el desplazamiento, o 22.8 cm.
8.4 Aumenta porque tuvo que ejercer una fuerza hacia abajo, haciendo un trabajo positivo, para tirar de la masa hacia abajo, y eso es igual al cambio en la energía potencial total.
8.5 2.83 N
8.6 F = 4.8 N, dirigida hacia el origen
8.7 0.033 m
8.8 b. A cualquier altura dada, la energía potencial gravitatoria es la misma que sube o baja, pero la energía cinética disminuye menos que la subida, ya que la resistencia del aire es disipativa y funciona negativamente. Por lo tanto, en cualquier altura, la velocidad que baja es menor que la velocidad que sube, por lo que debe tomar más tiempo bajar que subir.
8.9 constante U(x) = -1 J
8.10 a. sí, movimiento limitado a -1.055 m ≤ x ≤ 1.055 m; b. mismos puntos y tipos de equilibrio que en el ejemplo
8.11 x(t) = ± √(2E/k)sen[(√k/m)t] y v0 = ±√(2E/m)
1. La energía potencial de un sistema puede ser negativa porque su valor es relativo a un punto definido.
3. Si el punto de referencia del suelo es energía potencial gravitacional cero, la jabalina primero aumenta su energía potencial gravitacional, seguida de una disminución en su energía potencial gravitatoria a medida que se lanza hasta tocar el suelo. El cambio general en la energía potencial gravitatoria de la jabalina es cero a menos que el centro de masa de la jabalina sea más bajo que el lugar desde el que se lanza inicialmente, y por lo tanto tendría un poco menos de energía potencial gravitacional.
5. la altura vertical desde el suelo hasta el objeto
7. Una fuerza que quita energía del sistema que no puede recuperarse si revertimos la acción.
9. El cambio en la energía cinética es el trabajo neto. Como las fuerzas conservadoras son independientes del camino, cuando vuelves al mismo punto, las energías cinética y potencial son exactamente las mismas que al principio. Durante el viaje, la energía total se conserva, pero cambian tanto la energía potencial como la cinética.
11. El automóvil experimenta un cambio en la energía potencial gravitacional a medida que desciende por las colinas debido a que la distancia vertical está disminuyendo. Parte de este cambio de energía potencial gravitacional será eliminado por el trabajo realizado por la fricción. El resto de la energía da como resultado un aumento de la energía cinética, haciendo que el automóvil vaya más rápido. Por último, el automóvil frena y perderá su energía cinética en el trabajo realizado frenando hasta detenerse.
13. Declara que la energía total del sistema E se conserva siempre que no haya fuerzas no conservativas que actúen sobre el objeto.
15. Pone energía en el sistema a través de sus piernas comprimiéndose y expandiéndose.
17. Cuatro veces la altura original duplicaría la velocidad de impacto.
19. 40,000
21. a.-200 J; b.-200 J; c.-100 J; d.-300 J
23. a.0.068 J; b -0.068 J; c.0.068 J; d.0.068 J; e.-0.068 J; f.46 cm
25. a.-120 J; b.120 J
27. a. (-2ab)1/6; b. 0; c. ~x6
29. 14 m/s
31. 14 J
33. normal
35. 9.7 m/s
37. 39 m/s
39. 1900 J
41. 151 J
43. 3.5 cm
45. 10x con eje x apuntado lejos de la pared y origen en la pared
47. 4.6 m/s
49. a. 5,6 m/s; b. 5.2 m/s; c. 6.4 m/s; d. no; e. sido
51. a. donde k = 0.02, A = 1, α = 1; b. F = kx - αxAe-αx2; c. La energía potencial en x = 0 debe ser menor que la energía cinética más potencial en x = a o A ≤ 1/2mv2 + 1/2ka2 + Ae-αa2. Resolver esto para coincidencias A resulta en el problema.
53. 8700 N/m
55. a. 70,6 m/s; b. 69.9 m/s
57. a. 180 N/m; b. 11 m
59. a. 9.8 × 103 J; b. 1.4 × 103 J; c. 14 m/s
61. a. 47,6 m; b. 1,88 × 105 J; c. 373 N
63. 33.9 cm
65. a. Cero, ya que la energía total del sistema es cero y la energía cinética en el punto más bajo es cero; b. -0.038 J; c. 0.62 m/s
67. 42 cm
69. 0.44 J
71. 3.6 m/s
73. bD4/4
75. Normal
77.
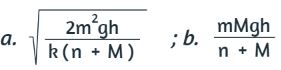
79. a. 2.24 m/s; b. 1.94 m/s; c. 1.94 m/s
81. 18 m/s
83. vA = 24 m/s; vB = 14 m/s; vC = 31 m/s
85. a. Pérdida de energía en 240 N•m; F = 8 N
87 89.7 m/s
89 32 J