Respuestas - Capítulo V
Comprueba tu aprendizaje
5.1 14 N, 56° medido desde el eje x positivo
5.2 a. Su peso actúa hacia abajo, y la fuerza de la resistencia del aire con el paracaídas actúa hacia arriba. b. ninguno; las fuerzas son iguales en magnitud
5.3 0.1 m/s2
5.4 40 m/s2
5.5 a. 159.0i^ + 770.0j^ N; b. 0.1590i^ + 0.7700j^ N
5.6 a = 2.78 m/s2
5.7 a. 3.0 m/s2; b. 18 N
5.8 a. 1,7 m/s2; b. 1.3 m/s2
5.9 6.0 × 102 N
5.10
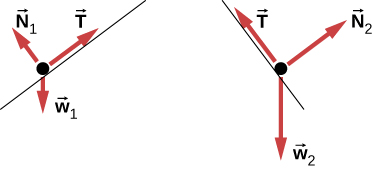
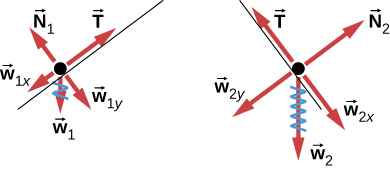
Preguntas conceptuales
1. Las fuerzas son direccionales y tienen magnitud.
3. La velocidad de las tortas antes de la acción de frenado fue la misma que la del auto. Por lo tanto, las tortas eran cuerpos sin restricciones en movimiento, y cuando el auto se detuvo de repente, siguieron avanzando según la primera ley de Newton.
5. No. Si la fuerza fuera cero en este punto, entonces no habría nada que cambie la velocidad cero momentánea del objeto. Como no observamos el objeto suspendido inmóvil en el aire, la fuerza no puede ser cero.
7. El astronauta es realmente ingrávido en la ubicación descrita, porque no hay un gran cuerpo (planeta o estrella) cerca para ejercer una fuerza gravitatoria. Su masa es de 70 kg, independientemente de dónde se encuentre.
9. La fuerza que ejerces (una fuerza de contacto igual en magnitud a tu peso) es pequeña. La tierra es extremadamente masiva en comparación. Por lo tanto, la aceleración de la Tierra sería increíblemente pequeña. Para ver esto, usa la segunda ley de Newton para calcular la aceleración que causaría si tu peso es 600.0 N y la masa de la Tierra es 6.00 × 1024 kg.
11. a. acción: la Tierra tira de la Luna, reacción: la Luna tira de la Tierra; b acción: el pie aplica fuerza a la pelota, reacción: la pelota aplica fuerza al pie; c. acción: el cohete empuja el gas, reacción: el gas empuja hacia atrás el cohete; d. acción: los neumáticos de los automóviles retroceden en la carretera, reacción: el camino empuja hacia delante los neumáticos; e. acción: el saltador empuja hacia abajo en el suelo, reacción: el suelo empuja hacia arriba al saltador; f. Acción: la pistola empuja hacia adelante a la bala, reacción: la bala empuja hacia atrás la pistola.
13. a. El rifle (caparazón sostenido por el rifle) ejerce una fuerza para expulsar la bala; la reacción a esta fuerza es la fuerza que la bala ejerce sobre el rifle (carcasa) en dirección opuesta. b. En un rifle sin retroceso, el proyectil no está asegurado en el rifle; por lo tanto, a medida que la bala se empuja para avanzar, la cáscara se empuja para expulsar desde el extremo opuesto del barril. c. No es seguro pararse detrás de un rifle sin retroceso.
15. a. Sí, la fuerza puede estar actuando a la izquierda; la partícula experimentaría desaceleración y perdería velocidad. b. Sí, la fuerza puede estar actuando hacia abajo porque su peso actúa hacia abajo incluso cuando se mueve hacia la derecha.
17. Dos fuerzas de diferentes tipos: el peso actúa hacia abajo y la fuerza normal actúa hacia arriba
Problemas
19. a. F→Neta = 5.0i^ + 10.0j^ N; b. la magnitud es FNeta = 11 N, y la dirección es θ = 63°
21. a. F→Neta = 660.0i^ + 150.0j^ N; b. FNeta = 676.6 N a θ = 12.8° desde la cuerda de David
23. a. F→Neta = 95.0i^ + 283j^ N; b. 299 N a 71° al noreste; c. F→DS = - (95.0i^ + 283j^) N
25. Al salir del reposo, el velocista alcanza una velocidad de v = 12.96 m/s, al final de la aceleración. Encontramos el tiempo para la aceleración usando x = 20.00 m = 0 + 0.5at12x = 20.00 m , o t1 = 3.086s. Para la velocidad mantenida, x2 = vt2, o t2 = x2/v = 80.00 m/12.96 m/s = 6.173 s. Tiempo total = 9.259 s
27. a. m = 56.0 kg; c. Si la fuerza puede ser ejercida sobre el astronauta por otra fuente (que no sea la nave espacial), entonces la nave espacial no experimentará un retroceso.
29. F→Neta = 4.12 × 105 N
31. a = 253 m/s2
33. F→Neta = F - f = ma ⇒ F = 1.26 × 103 N
35 v2 = v02 + 2ax ⇒ a = -7.80 m/s2
FNeta = -7.80 × 103 N
37. a. F→Neta = ma→ ⇒ a→ = 9.0i^ m/s2; b. La aceleración tiene una magnitud de 9.0 m/s2, entonces x = 110 m
39. 1.6i^ - 0.8j^ m/s2
41. a. wluna = mgluna, m = 10kg; b. La masa no cambia, entonces por lo que la masa del astronautatanto en la Tierra como en la Luna es de 150 kg.
43. a. Fh = 3.68 × 103 N; w = 7.35 × 103N y Fh/2 = 5 veces mayor que que el peso;
b. FNeta = 3750 N11.3 ° desde horizontalFnet = 3750 N, θ = 11.3° con la horizontal
45. w = 19.6 N; FNeta = 5.40 N; FNeta = ma ⇒ a = 2.70 m/s2
47. 0.60i^ - 8.4j^ m/s2
49. 497 N
51. a. FNeta = 2,64 × 107 N; b. La fuerza ejercida sobre la nave también es 2.64 × 107 N porque está opuesta a la dirección de movimiento de la concha.
53. Debido a que el peso del libro de historia es la fuerza ejercida por la Tierra en el libro de historia, lo representamos como F→EH = -14j^ N. Aparte de esto, el libro de historia interactúa solo con el libro de física. Como la aceleración del libro de historia es cero, la fuerza neta sobre ella es cero según la segunda ley de Newton: F→PH + F→EH = 0→, donde F→PH es la fuerza ejercida por el libro de física en el libro de historia. Por lo tanto, F→PH = -F→EH = - (- 14j^) N = 14j^ N. Encontramos que el libro de física ejerce una fuerza ascendente de magnitud 14 N en el libro de historia. El libro de física tiene tres fuerzas ejercidas sobre él: F→EP debido a la Tierra, F→HP debido al libro de historia, y F→DP debido al escritorio. Dado que el libro de física pesa 18 N, F→EP = -18j^ N. De la tercera ley de Newton, F→HP = -F→PH, entonces F→HP = -14j^ N. La segunda ley de Newton aplicada al libro de física da ΣF→ = 0→, o F→DP + F→EP + F→HP = 0→, entonces F→DP = - (- 18j) - (- 14j) = 32jN.F → DP = - (- 18j^) - (- 14j^) = 32j^ N. El escritorio ejerce una fuerza ascendente de 32 N en el libro de física. Para llegar a esta solución, aplicamos la segunda ley de Newton dos veces y la tercera ley de Newton una vez.
55. a. El diagrama de cuerpo libre de la polea 4:
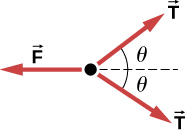
b. T = mg, F = 2Tcosθ = 2mgcosθ
57. a.

FNeta = Ma; F1 = 1350 N; F2 = 1365 N;
9( F2 - F1) = 9(m1 - m2)a; m1 = 68 kg; m2 = 73 kg
a = 0.11 m/s2
El equipo de más peso gana
b.
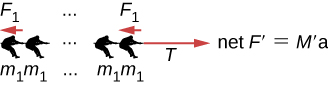
T − 9F1 = 9m1a ⇒ T = 9m1a + 9F1 = 1.2×104 N
59. a. T = 1.96 × 10-4 N;
b. T′ = 4.71 × 10-4 N
T′/T = 2.40 veces las tensión en el hilo vertical
61.
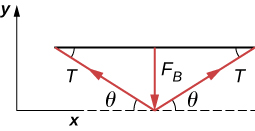
FyNeta = F⊥ − 2Tsenθ = 0
F⊥ = 2Tsenθ, T = F⊥/2senθ
63. a. Observa el ejemplo 5.13; b. 1.5 N; c. 15 N
65. a. 5.6 kg; b. 55 N; c. T2 = 60 N
d.
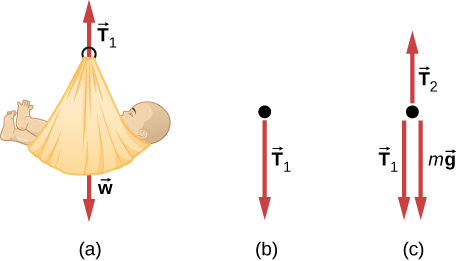
67. a. 4.9 m/s2, 17 N; b. 9.8 N
69.
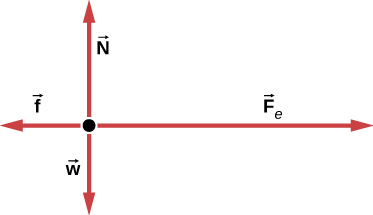
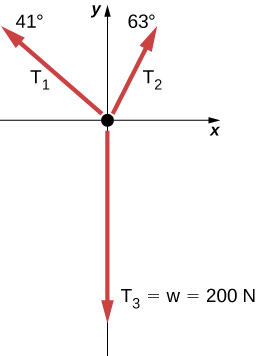
Problemas adicionales
73. 5.90 kg
75.

77. a. FNeta = m(v2 - v02)/2x; b. 2590 N
79. F→Neta = 4.05i^ +12.0j^ N
F→Neta = ma→ ⇒ a→ = 0.45i^ +1.20j^ m/s2
81.
F→Neta = F→A + F→B
F→Neta = Ai^ + (-1.41Ai^ - 1.41Aj^)
F→Neta = A(-0.41i^ - 1.41j^)
θ = 254°, (Añadimos 180°, porque el ángulo está en el cuadrante IV.)
83. F = 2kmx; Primero, toma la derivada de la función de velocidad para obtener a = 2kx. Luego aplica la segunda ley de Newton F = ma = m (2kx) = 2kmxF
85. a. Para el cuadro A, NA = mg y NA = mgcosθ; b. NA > NB porque para θ < 90°, cosθ <1; c. NA > NB cuando θ = 10°
87. a. 8.66 N; b. 0,433 m
89. 0,40 o 40%
91. 16 N
Problemas de Desafío
93. a.
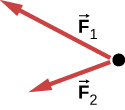
b. No; F→r no se muestra porque reemplazará a F→1 y F→2. (Si queremos mostrarlo, podríamos dibujarlo y luego colocar líneas onduladas en F→1 y F→2 para mostrar que ya no se consideran.)
95. a. 14.1 m/s; b. 601 N
97. F/mt2
99. 936 N
101. a→ = -248i^ - 433j^ m/s2
103. 0.548 m/s2
105. a. T1 = 2mg/sen θ, T2 = mg/sen(arctan(1/2tan θ)) + 1), T3 = 2mg/tan θ
b. ϕ = arctan(1/2tan θ)
c. 2.56°
d. x = d(2cos θ + 2cos(arctan(1/2tanθ)) +1 )
107. a. a→ = (5.00/mi^ + 3.00/mj^) m/s2
b. 1.38 kg
c. 21.2 m/s
d. v→ = (18.1i^ + 10.9j^) m/s2
109. a. 0.900i^ + 0.600j^ N
b. 1.08 N.










