Preguntas y problemas - Capítulo IX

Preguntas conceptuales

9.2 Momento lineal

1. Un objeto que tiene una masa pequeña y un objeto que tiene una masa grande tienen el mismo momento. ¿Qué objeto tiene la mayor energía cinética?

2. Un objeto que tiene una masa pequeña y un objeto que tiene una masa grande tienen la misma energía cinética. ¿Qué masa tiene el mayor momento?

9.3 Impulso y colisiones

3. ¿Es posible que una fuerza pequeña produzca un impulso mayor en un objeto dado que una fuerza grande? Explica.

4. ¿Por qué una caída de 10 m sobre el hormigón es mucho más peligrosa que una caída de 10 m sobre el agua?

5. ¿Qué fuerza externa es responsable de cambiar el momento de un automóvil que se mueve a lo largo de una carretera horizontal?

6. Una pieza de masilla y una pelota de tenis con la misma masa son lanzadas contra la pared con la misma velocidad. ¿Qué objeto experimenta un mayor impulso desde la pared o son los impulsos iguales? Explica.

9.4 Conservación del momento lineal

7. ¿En qué circunstancias se conserva el momento?

8. ¿Se puede conservar el momento para un sistema si hay fuerzas externas que actúan sobre el sistema? Si es así, ¿en qué condiciones? ¿Si no, porque no?

9. Explica en términos del momento y las leyes de Newton cómo la resistencia del aire de un automóvil se debe en parte al hecho de que empuja el aire en su dirección de movimiento.

10. ¿Pueden los objetos en un sistema tener momento mientras el momento del sistema es cero? Explica tu respuesta.

11. Un velocista acelera fuera de los tacos de salida. ¿Puedes considerarlo como un sistema cerrado? Explica.

12. Un cohete en el espacio profundo (gravedad cero) acelera al expulsar gas caliente de sus propulsores. ¿El cohete constituye un sistema cerrado? Explica.

9.5 Tipos de colisiones

13. Dos objetos de igual masa se mueven con velocidades iguales y opuestas cuando colisionan. ¿Se puede perder toda la energía cinética en la colisión?

14. Describe un sistema para el cual se conserva el momento, pero la energía mecánica no. Ahora al revés: describe un sistema para el cual se conserva la energía cinética, pero no el momento.

9.6 Colisiones en múltiples dimensiones

15. El momento para un sistema se puede conservar en una dirección mientras que no se conserva en otra. ¿Cuál es el ángulo entre las direcciones? Dar un ejemplo.

9.7 Centro de masa

16. Supongamos que explota un proyectil de fuegos artificiales, rompiéndose en tres piezas grandes para las cuales la resistencia del aire es insignificante. ¿Cómo afecta la explosión al movimiento del centro de masa? ¿Cómo se vería afectado si las piezas experimentaran significativamente más resistencia al aire que la carcasa del proyectil intacta?

9.8 Propulsión de cohetes

17. Es posible que la velocidad de un cohete sea mayor que la velocidad de escape de los gases que expulsa. Cuando ese es el caso, la velocidad del gas y el momento de gas están en la misma dirección que la del cohete. ¿Cómo es que el cohete todavía puede obtener empuje al expulsar los gases?

Problemas

9.2 Momento lineal

18. Un elefante y un cazador están teniendo una confrontación.



a. Calcula el momento del elefante de 2000.0 kg que ataca al cazador a una velocidad de 7.50 m/s.
b. Calcula la relación del momento del elefante al momento de un dardo tranquilizante de 0.0400 kg disparado a una velocidad de 600 m/s.
¿Cuál es el momento del cazador de 90.0 kg corriendo a 7.40 m/s después de perder al elefante?

19. Un patinador de 40 kg de peso lleva una caja de 5 kg de masa. El patinador tiene una velocidad de 5 m/s con respecto al piso y se desliza sin fricción sobre una superficie lisa.

a. Encuentra el momento de la caja con respecto al piso.
b. Encuentra el momento de la caja con respecto al piso después de colocar la caja sobre la superficie de patinaje sin fricción.

20. Un automóvil de masa 2000 kg se mueve con una velocidad constante de 10 m/s hacia el este. ¿Cuál es el momento del auto?

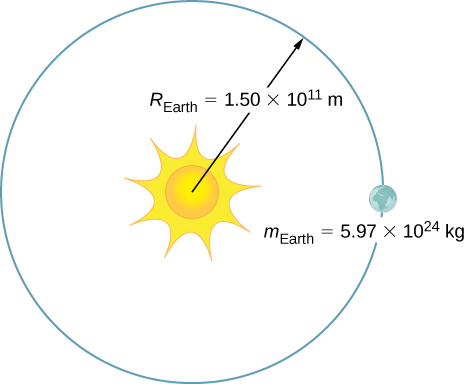
21. La masa de la Tierra es de 5,97 × 10²⁴ kg y su radio orbital es un promedio de 1,50 × 10¹¹ m. Calcula la magnitud de su momento lineal promedio



22. Si por una tormenta cae 1 cm de lluvia sobre un área de 10 km² en el período de 1 hora, ¿cuál es el momento de la lluvia que cae en un segundo? Supón que la velocidad terminal de una gota de lluvia es de 10 m/s.

23. ¿Cuál es el momento promedio de una avalancha que mueve una capa de nieve de 40 cm de espesor sobre un área de 100 m por 500 m en una distancia de 1 km por una colina en 5.5 s? Supón una densidad de 350 kg/m³ para la nieve.

24. ¿Cuál es el momento promedio de un velocista de 70.0 kg que corre la carrera de 100 m en 9.65 s?

9.3 Impulso y colisiones

25. Una persona de 75.0 kg viaja en un automóvil que se mueve a 20.0 m/s cuando el automóvil choca contra un estribo de puente (observa la siguiente figura).



Calcula la fuerza promedio sobre la persona si es detenido por un tablero acolchado que se comprime un promedio de 1.00 cm.
Calcula la fuerza promedio sobre la persona si es detenido por una bolsa de aire que se comprime un promedio de 15.0 cm.

26. Uno de los peligros de los viajes espaciales son los escombros que dejaron las misiones anteriores. Hay varios miles de objetos orbitando la Tierra que son lo suficientemente grandes como para ser detectados por el radar, pero hay un gran número de objetos muy pequeños, como trozos de pintura. Calcula la fuerza ejercida por un trozo de pintura de 0,100 mg que golpea la ventana de una nave espacial a una velocidad relativa de 4,00 × 10³ m/s, dado que la colisión dura 6,00 × 10^-8 s.

27. Un crucero con una masa de 1.00 × 10⁷ kg golpea un muelle a una velocidad de 0.750 m/s. Se detiene después de viajar 6.00 m, dañando el barco, el muelle y las finanzas del capitán del remolcador. Calcula la fuerza promedio ejercida en el muelle utilizando el concepto de impulso. (Sugerencia: primero calcula el tiempo que le tomó a la nave frenar, asumiendo una fuerza constante).



28. Calcula la velocidad final de un jugador de rugby de 110 kg que corre inicialmente a 8.00 m/s pero colisiona de frente con un poste abullonado y experimenta una fuerza hacia atrás de 1.76 × 10⁴ N para 5.50 × 10^-2 s.

29. El agua de una manguera contra incendios se dirige horizontalmente contra una pared a una tasa de 50.0 kg/sy una velocidad de 42.0 m/s. Calcula la fuerza ejercida sobre la pared, suponiendo que el momento horizontal del agua se reduce a cero.

30. Un martillo de 0,450 kg se mueve horizontalmente a 7,00 m/s cuando golpea un clavo y se detiene después de clavar el clavo a 1,00 cm en un tablero. Supón una aceleración constante del par de martillo-clavo.

a. Calcula la duración del impacto.
¿Cuál fue la fuerza promedio ejercida sobre el clavo?

31. ¿Cuál es el momento (en función del tiempo) de una partícula de 5.0 kg que se mueve con una velocidad v→(t) = (2.0i^ + 4.0tj^) m/s? ¿Cuál es la fuerza neta que actúa sobre esta partícula?

32. La componente x de una fuerza en una pelota de golf de 46 g con un "palo 7" en función del tiempo se traza en la siguiente figura:



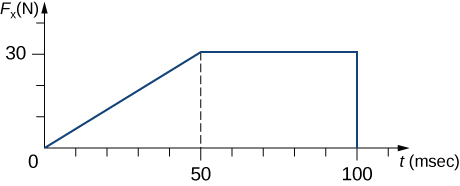
a. Encuentra la componente x del impulso durante los intervalos

i. [0, 50 ms], y
ii. [50 ms, 100 ms]

b. Encuentra el cambio en la componente x del momento durante los intervalos

iii. [0, 50 ms], y
iv. [50 ms, 100 ms]

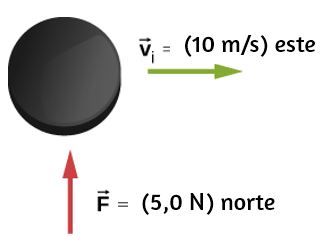
33. Un disco de hockey de 150 g de peso se desliza hacia el este sobre una mesa sin fricción con una velocidad de 10 m/s. De repente, una fuerza constante de magnitud 5 N y dirección hacia el norte se aplica al disco durante 1,5 s. Encuentre los componentes norte y este del momento al final del intervalo de 1.5 s



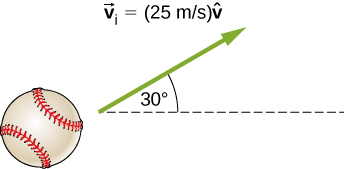
34. Se lanza una bola de masa de 250 g con una velocidad inicial de 25 m/s en un ángulo de 30° con la dirección horizontal. Ignora la resistencia del aire. ¿Cuál es el momento de la pelota después de 0.2 s? (Haz este problema buscando primero las componentes del momento y luego construyendo la magnitud y dirección del vector de momento a partir de las componentes).

9.4 Conservación del momento lineal

35. Los vagones del tren se acoplan al chocar entre sí. Supongamos que dos vagones cargados se mueven uno hacia el otro, el primero tiene una masa de 1.50 × 10⁵ kg y una velocidad de (0.30 m/s)i^, y el segundo tiene una masa de 1.10 × 10⁵ kg y una velocidad de -(0.12 m/s)i^. ¿Cuál es su velocidad final?



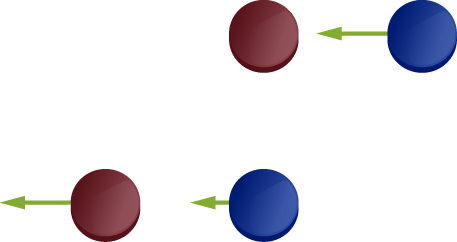
36. Dos discos idénticos colisionan elásticamente en una mesa de hockey de aire. El disco 1 originalmente estaba en reposo; el disco 2 tiene una velocidad de entrada de 6.00 m/s y se dispersa en un ángulo de 30° con respecto a su dirección entrante. ¿Cuál es la velocidad (magnitud y dirección) del disco 1 después de la colisión?



37. La figura siguiente muestra una bala de masa de 200 g que viaja horizontalmente hacia el este con una velocidad de 400 m/s, que golpea un bloque de masa de 1,5 kg que está inicialmente en reposo sobre una mesa sin fricción.



Después de golpear el bloque, la bala se incrusta en el bloque y el bloque y la bala se mueven juntos como una unidad.

a. ¿Cuál es la magnitud y la dirección de la velocidad de la combinación bloque/bala inmediatamente después del impacto?
b. ¿Cuál es la magnitud y la dirección del impulso dado por el bloque en la bala?
c. ¿Cuál es la magnitud y la dirección del impulso dado por la bala en el bloque?
d. Si la bala tardó 3 ms en cambiar la velocidad de 400 m/s a la velocidad final después del impacto, ¿cuál es la fuerza promedio entre el bloque y la bala durante este tiempo?

38. Un niño de 20 kg se está deslizando a 3,3 m/s sobre terreno llano en un vagón de 4,0 kg. El niño tira una bola de 1.0 kg en la parte trasera del vagón. ¿Cuál es la velocidad final del niño y el vagón?

39. Un camión de pavimentación de 5000 kg (masa que excluye la grava) recorre una carretera a 2,5 m/s y rápidamente arroja 1000 kg de grava en la carretera hacia atrás a 0,5 m/s. ¿Cuál es la velocidad del camión después de tirar la grava?

40. Explica por qué un cañón retrocede cuando dispara un proyectil.

41. Dos patinadores artísticas están patinando en la misma dirección, con el patinador principal moviéndose a 5.5 m/s y la patindora posterior moviéndose a 6.2 m/s. Cuando la patinadora que va detrás se pone al corriente con el patinador principal, la levanta sin aplicar fuerzas horizontales en sus patines. Si el patinador final es un 50% más pesado que el patinador principal de 50 kg, ¿cuál es su velocidad después de que él la levante?

42. Un vagón de carga ferroviario de 2000 kilogramos va a 4,4 m/s debajo de un terminal de granos, que vierte el grano directamente en el vagón de carga. Si la velocidad del vagón de carga cargado no debe ser inferior a 3,0 m/s, ¿cuál es la masa máxima de grano que puede aceptar?

9.5 Tipos de colisiones

43. Una bola de bolos de 5.50 kg que se mueve a 9.00 m/s colisiona con un boliche de 0.850 kg, que se dispersa en un ángulo con respecto a la dirección inicial de la bola de boliche y con una velocidad de 15.0 m/s.

a. Calcula la velocidad final (magnitud y dirección) de la bola de boliche.
b. ¿La colisión es elástica?

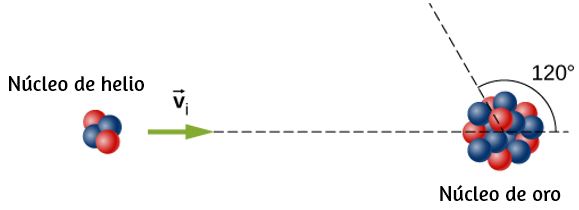
44. Ernest Rutherford (el primer neozelandés que recibió el Premio Nobel de Química) demostró que los núcleos eran muy pequeños y densos al dispersar núcleos de helio-4 de núcleos de oro-197. La energía del núcleo entrante de helio fue de 8.00 × 10^-13 J, y las masas de los núcleos de helio y oro fueron 6.68 × 10^-27 kg y 3.29 × 10^-25 kg, respectivamente (obsérva que su relación de masa es de 4 a 197).

a. Si un núcleo de helio se dispersa en un ángulo de 120° durante una colisión elástica con un núcleo de oro, calcula la velocidad final del núcleo de helio y la velocidad final (magnitud y dirección) del núcleo de oro.
b. ¿Cuál es la energía cinética final del núcleo de helio?



45. Un jugador de hockey sobre hielo de 90.0 kg golpea un disco de 0.150 kg, dando al disco una velocidad de 45.0 m/s. Si ambos están inicialmente en reposo y si el hielo no tiene fricción, ¿hasta qué punto retrocede el jugador en el tiempo que tarda el disco en alcanzar la meta a 15.0 m de distancia?

46. ​​Un petardo de 100 g se lanza verticalmente en el aire y explota en dos pedazos en la cima de su trayectoria. Si una pieza de 72 g se proyecta horizontalmente hacia la izquierda a 20 m/s, ¿cuál es la velocidad y la dirección de la otra pieza?

47. En una colisión elástica, un parachoques de 400 kg colisiona directamente desde atrás con un segundo paragolpes idéntico que viaja en la misma dirección. La velocidad inicial del paragolpes delantero es de 5,60 m/s, y la del vehículo trasero es de 6,00 m/s. Suponiendo que la masa de los conductores es mucho, mucho menos que la de los autos de choque, ¿cuáles son sus velocidades finales?

48. Repite el problema anterior si la masa del paragolpes delantero es 30.0% mayor que la del paragolpes trasero.

49. Una partícula alfa (4He) sufre una colisión elástica con un núcleo de uranio estacionario (235U). ¿Qué porcentaje de la energía cinética de la partícula alfa se transfiere al núcleo de uranio? Supongamos que la colisión es unidimensional.

50. Estás de pie sobre una superficie helada resbaladiza y lanzas una pelota de fútbol de 1 kg horizontalmente a una velocidad de 6.7 m/s. ¿Cuál es tu velocidad cuando lanzas el balón? Supón que su masa es de 65 kg.

51. Un niño de 35 kg baja en trineo colina abajo y luego se desliza a lo largo de la sección plana en la parte inferior, donde un segundo niño de 35 kg salta sobre el trineo cuando pasa junto a él. Si la velocidad del trineo es de 3.5 m/s antes de que el segundo niño salte, ¿cuál es la velocidad después de que salta?

52. Un niño baja en trineo colina abajo y cae sobre un lago cubierto de hielo sin fricción a 10.0 m/s. En el medio del lago hay una roca de 1000 kg. Cuando el trineo se estrella contra la roca, es impulsado sobre la roca y continúa deslizándose sobre el hielo. Si la masa del niño es de 40.0 kg y la masa del trineo es de 2.50 kg, ¿cuál es la velocidad del trineo y la roca después de la colisión?

9.6 Colisiones en múltiples dimensiones

53. Un halcón de 1.80 kg vuela a 28.0 m/s en un ángulo descendente de 35°. Captura una paloma de 0.650 kg desde atrás en el aire. ¿Cuál es su velocidad combinada después del impacto si la velocidad inicial de la paloma era 7.00 m/s dirigida horizontalmente? Ten en cuenta que v^_1,i es un vector unitario que apunta en la dirección en la que el halcón está volando inicialmente.



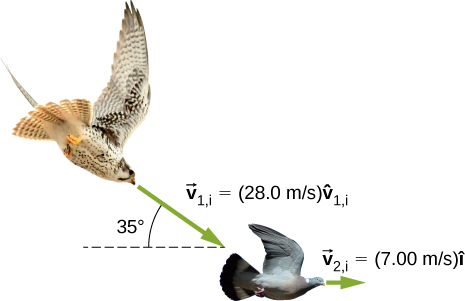
Figura 9.34 (crédito "halcón": modificación del trabajo por "USFWS Mountain-Prairie" / Flickr; crédito "paloma": modificación del trabajo por Jacob Spinks)

54. Una bola de billar, marcada con un 1, que se mueve horizontalmente golpea otra bola de billar, etiquetada con el 2, en reposo. Antes del impacto, la bola 1 se movía a una velocidad de 3,00 m/s, y después del impacto se movía a 0,50 m/s a 50° de la dirección original. Si las dos bolas tienen masas iguales de 300 g, ¿cuál es la velocidad de la bola 2 después del impacto?

55. Un proyectil de 2.0 kg de masa se dispara en el aire con un ángulo de 40.0° con respecto a la horizontal a una velocidad de 50.0 m/s. En el punto más alto de su vuelo, el proyectil se rompe en tres partes de masa 1.0 kg, 0.7 kg y 0.3 kg. La pieza de 1.0 kg cae hacia abajo después de la ruptura con una velocidad inicial de 10.0 m/s, la pieza de 0.7 kg se mueve en la dirección original hacia adelante, y la pieza de 0.3 kg va hacia arriba.



a. Encuentra las velocidades de las piezas de 0.3 kg y 0.7 kg inmediatamente después de la ruptura.
b. ¿Qué tan alto desde el punto de ruptura va la pieza de 0,3 kg antes de detenerse?
c. ¿Dónde aterriza la pieza de 0.7 kg en relación con el lugar desde el que fue disparada?

56. Dos asteroides colisionan y se unen. El primer asteroide tiene una masa de 15 × 10³ kg y se mueve inicialmente a 770 m/s. El segundo asteroide tiene una masa de 20 × 10³ kg y se mueve a 1020 m/s. Sus velocidades iniciales formaban un ángulo de 20° con respecto a la otra. ¿Cuál es la velocidad y dirección final con respecto a la velocidad del primer asteroide?

57. Un cohete de 200 kg en el espacio profundo se mueve con una velocidad de (121 m/s)i^ + (38.0 m/s) j^. De repente, explota en tres pedazos, con el primero (78 kg) moviéndose a - (321 m/s)i^ + (228 m/s)j^ y el segundo (56 kg) moviéndose a (16.0 m/s)i^ - (88.0 m/s)j^. Encuentra la velocidad de la tercera pieza.

58. Un protón que viaja a 3,0 × 10⁶ m/s colisiona elásticamente con una partícula alfa inicialmente en reposo y se desvía en un ángulo de 85° con respecto a su velocidad inicial. Dado que la partícula alfa tiene cuatro veces la masa del protón, ¿qué porcentaje de su energía cinética inicial conserva el protón después de la colisión?

59. Tres ciervos de 70 kg están de pie sobre una roca plana de 200 kg que se encuentra en un estanque cubierto de hielo. Se dispara un proyectil propiciando una dispersión, con el ciervo A corriendo a (15 m/s)i^ + (5.0 m/s)j^, el ciervo B corriendo a (-12 m/s)i^ + (8.0 m/s)j^, y el ciervo C corriendo a (1.2 m/s)i^ - (18.0 m/s)j^. ¿Cuál es la velocidad de la roca sobre la que estaban parados?

60. Una familia está patinando. El padre (75 kg) patina a 8,2 m/s, choca y se pega a la madre (50 kg), que inicialmente se movía a 3,3 m/s y a 45° con respecto a la velocidad del padre. El par choca con su hija (30 kg), que estaba inmóvil, y los tres se deslizan juntos. ¿Cuál es su velocidad final?

61. Un átomo de oxígeno (masa 16 u) que se mueve a 733 m/s a ​​15.0° con respecto a la dirección i^ colisiona y se adhiere a una molécula de oxígeno (masa 32 u) moviéndose a 528 m/s a ​​128° con respecto a la dirección i^. Los dos se unen para formar ozono. ¿Cuál es la velocidad final de la molécula de ozono?

62. Dos automóviles se acercan a una intersección perpendicular de cuatro vías extremadamente helada. El automóvil A viaja hacia el norte a 30 m/s y el automóvil B viaja hacia el este. Chocan y se unen, viajando a 28° al noreste. ¿Cuál fue la velocidad inicial del auto B?

9.7 Centro de masa

63. Tres masas puntuales se colocan en las esquinas de un triángulo como se muestra en la figura a continuación.



Encuentra el centro de masa del sistema de tres masas.

64. Dos partículas de masas m₁ y m₂ separadas por una distancia horizontal D se liberan desde la misma altura h al mismo tiempo. Encuentra la posición vertical del centro de masa de estas dos partículas a la vez antes de que las dos partículas toquen el suelo. Suponer que no hay resistencia al aire.

65. Dos partículas de masas m₁ y m₂ separadas por una distancia horizontal D se sueltan desde la misma altura h en diferentes momentos. La partícula 1 comienza en t = 0, y la partícula 2 se suelta en t = T. Encuentra la posición vertical del centro de masa a la vez antes de que la primera partícula toque el suelo. Suponer que no hay resistencia al aire.

66. Dos partículas de masas m₁ y m₂ se mueven uniformemente en diferentes círculos de radios R₁ y R₂ sobre el origen en el plano x, y. Las coordenadas x e y del centro de masa y la de la partícula 1 se dan de la siguiente manera (donde la longitud es en metros y t en segundos):

x₁(t) = 4cos(2t), y₁(t) = 4sen(2t), y

x_CM(t) = 3cos(2t), y_CM(t) = 3sen(2t).

a. Encuentra el radio del círculo en el que se mueve la partícula 1.
b. Encuentra las coordenadas x e y de la partícula 2 y el radio del círculo que mueve esta partícula.

67. Dos partículas de masas m₁ y m₂ se mueven uniformemente en diferentes círculos de radios R₁ y R₂ sobre el origen en el plano x, y. Las coordenadas de las dos partículas en metros se dan de la siguiente manera (z = 0 para ambos). Aquí t está en segundos:

x₁(t) = 4cos(2t)
y₁(t) = 4sen(2t)
x₂(t) = 2cos(3t − π/2)
y₂(t) = 2sen(3t − π/2)

a. Encuentra los radios de los círculos de movimiento de ambas partículas.
b. Encuentra las coordenadas x e y del centro de masa.
c. Decide si el centro de masa se mueve en un círculo al trazar su trayectoria.

68. Encuentra el centro de masa de una varilla de un metro de longitud, hecha de 50 cm de hierro (densidad 8 g/cm³) y 50 cm de aluminio (densidad 2,7 g/cm³).

69. Encuentra el centro de masa de una vara de longitud L cuya densidad de masa cambia de un extremo al otro de forma cuadrática. Es decir, si la varilla está dispuesta a lo largo del eje x con un extremo en el origen y el otro extremo en x = L, la densidad está dada por ρ(x) = ρ₀ + (ρ₁ - ρ₀)(x/L)², donde ρ₀ y ρ₁ son valores constantes.

70. Encuentra el centro de masa de un bloque rectangular de longitud a y ancho b que tiene una densidad no uniforme de modo que cuando el rectángulo se coloca en el plano xy con una esquina en el origen y el bloque colocado en el primer cuadrante con los dos bordes a lo largo de los ejes x e y, la densidad viene dada por ρ(x, y) = ρ₀x, donde ρ₀ es una constante.

71. Encuentra el centro de masa de un material rectangular de longitud a y ancho b formado por un material de densidad no uniforme. La densidad es tal que cuando el rectángulo se coloca en el plano xy, la densidad viene dada por ρ(x, y) = ρ₀xy.

72. Un cubo de lado a se corta de otro cubo de lado b como se muestra en la figura a continuación.



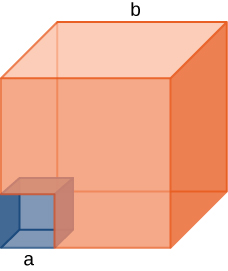
Encuentra la ubicación del centro de masa de la estructura. (Sugerencia: piensa en la parte faltante como una masa negativa que se superpone a una masa positiva).

73. Encuentra el centro de masa de un cono de densidad uniforme que tiene un radio R en la base, altura h y masa M. Deja que el origen esté en el centro de la base del cono y que + z atraviese el cono vértice.

74. Encuentra el centro de masa de un cable delgado de masa m y largo L doblado en forma semicircular. Deja que el origen esté en el centro del semicírculo y traza el arco de alambre desde el eje + x, cruce el eje + y, y termine en el eje -x.

75. Encuentra el centro de masa de una placa semicircular fina y uniforme de radio R. Deja que el origen esté en el centro del semicírculo, el arco de la placa desde el eje + x al eje -x, y el eje z sea perpendicular a la placa.

76. Encuentra el centro de masa de una esfera de masa M y radio R y un cilindro de masa m, radio r y altura h dispuestos como se muestra a continuación



Expresa tus respuestas en un sistema de coordenadas que tiene el origen en el centro del cilindro.

9.8 Propulsión de cohetes

77. (a) Un calamar de 5.00 kg inicialmente en reposo expulsa 0.250 kg de fluido con una velocidad de 10.0 m/s. ¿Cuál es la velocidad de retroceso del calamar si la eyección se realiza en 0.100 s y hay una fuerza de fricción de 5.00 N que se opone al movimiento del calamar? (b) ¿Cuánta energía se pierde en el trabajo realizado contra la fricción?

78. Un cohete despega de la Tierra y alcanza una velocidad de 100 m/s en 10.0 s. Si la velocidad de escape es de 1500 m/s y la masa de combustible quemado es de 100 kg, ¿cuál fue la masa inicial del cohete?

79. Repite el problema anterior excepto para un cohete que despega de una estación espacial, donde no hay gravedad más que la gravedad insignificante debida a la estación espacial.

80. ¿Cuánto combustible se necesitaría para un cohete de 1000 kg (esta es su masa sin combustible) para despegar de la Tierra y alcanzar los 1000 m/s en 30 s? La velocidad de escape es 1000 m/s.

81. ¿Qué velocidad de escape se requiere para acelerar un cohete en el espacio profundo de 800 m/s a ​​1000 m/s en 5.0 s si la masa total del cohete es de 1200 kg y al cohete solo le quedan 50 kg de combustible?

82. Resultados irrazonables. Se informó que los calamares saltan del océano y viajan 30.0 m (medidos horizontalmente) antes de volver a ingresar al agua. (a) Calcula la velocidad inicial del calamar si sale del agua en un ángulo de 20.0°, suponiendo un levantamiento insignificante en el aire y una resistencia al aire insignificante. (b) El calamar se propulsa arrojando agua. ¿Qué fracción de su masa tendría que expulsar para alcanzar la velocidad encontrada en la parte anterior? El agua es expulsada a 12.0 m/s; la fuerza gravitatoria y la fricción están despreciads. (c) ¿Qué es irracional sobre los resultados? (d) ¿Qué premisa no es razonable o qué premisas son inconsistentes?

Problemas adicionales

83. Dos canoeros de 70 kg reman en una sola canoa de 50 kg. Su remo mueve la canoa a 1.2 m/s con respecto al agua, y el río en el que fluyen a 4 m/s con respecto a la tierra. ¿Cuál es su momento con respecto a la tierra?

84. ¿Cuál tiene una mayor magnitud de momento: un elefante de 3000 kg moviéndose a 40 km/h o un guepardo de 60 kg moviéndose a 112 km/h?

85. Un conductor aplica los frenos y reduce la velocidad de su automóvil en un 20%, sin cambiar la dirección en la que se mueve el automóvil. ¿Por cuánto cambia el momento del automóvil?

86. Tu amigo afirma que el momento es la masa multiplicada por la velocidad, por lo que las cosas con más masa tienen más momento. ¿Estás de acuerdo? Explica.

87. Dejar caer un vaso sobre un piso de cemento es más probable que rompa el vidrio que si se cae desde la misma altura sobre un césped. Explica en términos del impulso.

88. Tu automóvil deportivo de 1500 kg acelera de 0 a 30 m/s en 10 s. ¿Qué fuerza promedio se ejerce sobre él durante esta aceleración?

89. Se cae una bola de masa m. ¿Cuál es la fórmula del impulso que se ejerce sobre la pelota desde el momento en que se deja caer en un tiempo arbitrario τ más tarde? Ignora la resistencia del aire.

90. Repite el problema anterior, pero incluyendo una fuerza de arrastre debida al aire de f_drag = -bv→.

91. Un huevo de 5.0 g cae de un mostrador de 90 cm de altura sobre el piso y se rompe. ¿Qué impulso ejerce el piso sobre el huevo?

92. Un automóvil choca contra un árbol grande que no se mueve. El auto va de 30 m/s a ​​0 en 1.3 m. (a) ¿Qué impulso se aplica al conductor por el cinturón de seguridad, suponiendo que sigue el mismo movimiento que el automóvil? (b) ¿Cuál es la fuerza promedio aplicada al conductor por el cinturón de seguridad?

93. Dos jugadores de hockey se aproximan uno al otro, cada uno viajando a la misma velocidad v_i. Chocan y se enredan, caen y se mueven a una velocidad v_i/ 5. ¿Cuál es la proporción de sus masas?

94. Estás paseando en tu bicicleta de 10 kg a 15 m/s y un bicho de 5.0 g golpea en tu casco. El bicho se movía inicialmente a 2.0 m/s en la misma dirección que tú. Si tu masa es de 60 kg, (a) ¿cuál es tu momento inicial más el de tu bicicleta? (b) ¿Cuál es el momento inicial del bicho? (c) ¿Cuál es su cambio en la velocidad debido a la colisión con el bicho? (d) ¿Cuál hubiera sido el cambio en la velocidad si el bicho hubiera viajado en la dirección opuesta?

95. Una carga de grava se vierte directamente en un vagón de mercancías de 30000 kg que navega a 2,2 m/s en una sección recta de un ferrocarril. Si la velocidad del vagón de carga después de recibir la grava es de 1.5 m/s, ¿qué masa de grava recibió?

6. Dos carros en línea recta colisionan de frente. El primer carro se movía a 3.6 m/s en la dirección x positiva y el segundo se movía a 2.4 m/s en la dirección opuesta. Después de la colisión, el segundo automóvil continúa moviéndose en su dirección inicial de movimiento a 0,24 m/s. Si la masa del segundo automóvil es 5.0 veces la del primero, ¿cuál es la masa y la velocidad final del primer automóvil?

97. Un astronauta de 100 kg se encuentra separado de su nave espacial por 10 m y se aleja de la nave espacial a 0.1 m/s. Para volver a la nave espacial, lanza una bolsa de herramientas de 10 kg desde la nave espacial a 5.0 m/s. ¿Cuánto tiempo tardará en regresar a la nave espacial?

98. Deriva las ecuaciones que dan las velocidades finales para dos objetos que colisionan elásticamente, siendo la masa de los objetos m₁ y m₂ y las velocidades iniciales v_1,i y v_2,i = 0 (es decir, el segundo objeto está inicialmente en reposo).

99. Repite el problema anterior para el caso cuando la velocidad inicial del segundo objeto es distinta de cero.

100. Un niño baja en trineo colina abajo y colisiona a 5,6 m/s con un trineo en reposo idéntico al suyo. El niño se lanza hacia adelante a la misma velocidad, dejando atrás los dos trineos que se unen y se deslizan hacia adelante más lentamente. ¿Cuál es la velocidad de los dos trineos después de esta colisión?

101. Para el problema anterior, encuentra la velocidad final de cada trineo para el caso de una colisión elástica.

102. Un jugador de fútbol de 90 kg salta verticalmente en el aire para atrapar un balón de fútbol de 0,50 kg que se lanza esencialmente horizontal a 17 m/s. ¿Cuál es su velocidad horizontal después de atrapar la pelota?

103. Tres paracaidistas están cayendo en picado hacia la tierra. Inicialmente se están sosteniendo el uno al otro, pero luego se separan. Dos paracaidistas con una masa de 70 y 80 kg obtienen velocidades horizontales de 1.2 m/s norte y 1.4 m/s sureste, respectivamente. ¿Cuál es la velocidad horizontal del tercer paracaidista, cuya masa es de 55 kg?

104. Dos bolas de billar están en reposo y se tocan en una mesa de billar. La bola blanca viaja a 3.8 m/s a ​​lo largo de la línea de simetría entre estas bolas y las golpea simultáneamente. Si la colisión es elástica, ¿cuál es la velocidad de las tres bolas después de la colisión?

105. Una bola de billar que viaja a (2.2 m/s)i^ - (0.4 m/s)j^ colisiona con una pared que está alineada en la dirección j^. Suponiendo que la colisión es elástica, ¿cuál es la velocidad final de la pelota?

106. Dos bolas de billar idénticas colisionan. La primera está viajando inicialmente a (2.2 m/s)i^ - (0.4 m/s)j^ y la segunda a - (1.4 m/s)i^ + (2.4 m/s)j^. Supongamos que colisionan cuando el centro de la bola 1 está en el origen y el centro de la bola 2 está en el punto (2R, 0) donde R es el radio de las bolas. ¿Cuál es la velocidad final de cada bola?

107. Repite el problema anterior si las bolas chocan cuando el centro de la bola 1 está en el origen y el centro de la bola 2 está en el punto (0, 2R).

108. Repite el problema anterior si las bolas chocan cuando el centro de la bola 1 está en el origen y el centro de la bola 2 está en el punto (√3R/2, R/2)

109. ¿Dónde está el centro de masa de un cable semicircular de radio R que se centra en el origen, comienza y termina en el eje x, y se encuentra en el plano xy?

110. ¿Dónde está el centro de masa de una porción de pizza cortada en ocho porciones iguales? Supón que el origen está en el vértice del corte y mide ángulos con respecto a un borde del corte. El radio de la pizza es R.

111. Si toda la población de la Tierra fuera transferida a la Luna, ¿hasta dónde se movería el centro de masa del sistema Tierra-Luna? Supongamos que la población es de 7 mil millones, el humano promedio tiene una masa de 65 kg y que la población está distribuida uniformemente tanto en la Tierra como en la Luna. La masa de la Tierra es de 5,97 × 10²⁴ kg y la de la Luna es de 7,34 × 10²² kg. El radio de la órbita de la Luna es de aproximadamente 3.84 × 10⁵ m.

112. Tu amigo te pregunta cómo un cohete sigue subiendo al cielo una vez que está lo suficientemente alto sobre la superficie de la Tierra de tal froma que sus gases expulsados ​​ya no empujen en la superficie. ¿Cómo respondes?

113. Para aumentar la aceleración de un cohete, ¿deberías arrojar piedras desde la ventana frontal del cohete o desde la ventana trasera?

Problemas desafío

114. Una persona de 65 kg salta desde la ventana del primer piso de un edificio en llamas y aterriza casi verticalmente en el suelo con una velocidad horizontal de 3 m/s y una velocidad vertical de -9 m/s. Al impactar contra el suelo, se detiene en poco tiempo. La fuerza que experimentan sus pies depende de si mantiene las rodillas rígidas o las dobla. Encuentra la fuerza de sus pies en cada caso.



a. Primero encuentra el impulso sobre la persona del impacto en el suelo. Calcula tanto su magnitud como su dirección.
b. Encuentra la fuerza promedio en los pies si la persona mantiene su pierna rígida y recta y su centro de masa cae solo 1 cm verticalmente y 1 cm horizontalmente durante el impacto.
c. Encuentra la fuerza promedio en los pies si la persona dobla sus piernas durante el impacto de manera que su centro de masa caiga en 50 cm verticalmente y 5 cm horizontalmente durante el impacto.
d. Compara los resultados de la parte (b) y (c) y saca conclusiones sobre qué camino es mejor.

Necesitarás encontrar el tiempo que dura el impacto haciendo suposiciones razonables sobre la desaceleración. Aunque la fuerza no es constante durante el impacto, es aceptable trabajar con una fuerza promedio constante para este problema.

115. Dos proyectiles de masa m₁ y m₂ se disparan a la misma velocidad pero en direcciones opuestas desde dos sitios de lanzamiento separados por una distancia D. Ambas alcanzan el mismo punto en su punto más alto y golpean allí. Como resultado del impacto, se unen y se mueven como un solo cuerpo después. Encuentra el lugar donde aterrizarán.

116. Dos objetos idénticos (como bolas de billar) tienen una colisión unidimensional en la que uno está inicialmente inmóvil. Después de la colisión, el objeto en movimiento queda en reposo y el otro se mueve con la misma velocidad que el otro originalmente. Demostrar que tanto el momento como la energía cinética se conservan.

117. Una rampa de masa M está en reposo sobre una superficie horizontal. Un pequeño carro de masa m se coloca en la parte superior de la rampa y se suelta.



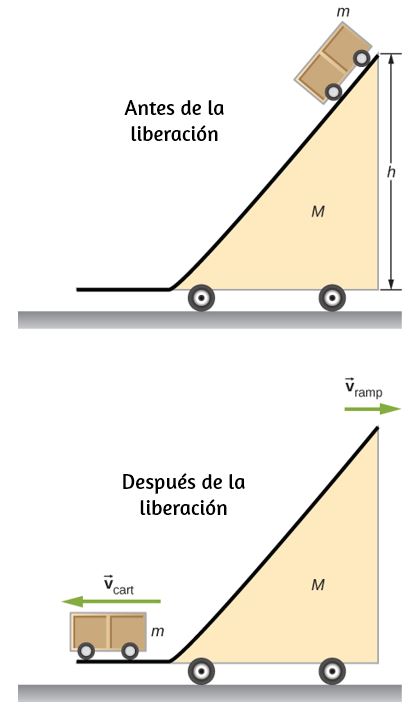
¿Cuáles son las velocidades de la rampa y el carro en relación con el suelo en el instante en que el carro sale de la rampa?

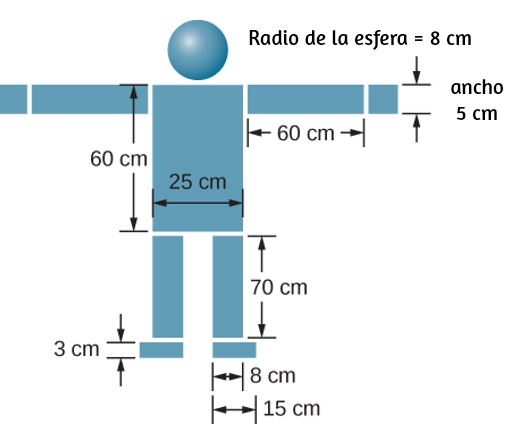
118. Encuentra el centro de masa de la estructura dada en la siguiente figura. Supón un espesor uniforme de 20 cm y una densidad uniforme de 1 g/cm³.