Preguntas y problemas - Capítulo VII

Preguntas conceptuales

7.2 Trabajo

1. Describe un ejemplo de algo que consideramos trabajo en circunstancias cotidianas que no es trabajo en el sentido científico. ¿La energía se transfiere o cambia de forma en tu ejemplo? Si es así, explica cómo se logra esto sin hacer el trabajo.

2. Describe un ejemplo de una situación en la que hay una fuerza y un desplazamiento, pero la fuerza no funciona. Explica por qué no funciona.

3. Describe una situación en la que se ejerce una fuerza durante un tiempo prolongado pero no funciona. Explica.

4. Un cuerpo se mueve en un círculo a velocidad constante. ¿Funciona la fuerza centrípeta que acelera el cuerpo? Explica.

5. Supongamos que arrojas una pelota hacia arriba y la atrapas cuando vuelve a la misma altura. ¿Cuánto trabajo hace la fuerza gravitatoria en la pelota durante todo el viaje?

6. ¿Por qué es más difícil hacer sentadillas en una tabla inclinada que en una superficie horizontal? (Observa la figura.)



7. Cuando era joven, Tarzán subió a una parra para llegar a la casa de su árbol. A medida que crecía, decidió construir y usar una escalera. Dado que el trabajo de la fuerza gravitatoria mg es independiente del camino, ¿qué ganó el Rey de los Monos al usar las escaleras?

7.3 Energía cinética

8. Una partícula de m tiene una velocidad de v_xi^ + v_yj^ + v_zk^. ¿Su energía cinética está dada por m(v_x²i^ + v_y²j^ + v_z²k^)/2? Si no, ¿cuál es la expresión correcta?

9. Una partícula tiene masa m y una segunda partícula tiene masa 2m. La segunda partícula se mueve con la velocidad v y la primera con la velocidad 2v. ¿Cómo se comparan sus energías cinéticas?

10. Una persona arroja un guijarro de masa m₁ desde una altura h, y golpea el piso con energía cinética K. La persona deja caer otro guijarro de masa m₂ desde una altura de 2h, y golpea el piso con la misma energía cinética K ¿Cómo se comparan las masas de los guijarros?

7.4 Teorema del trabajo-energía

11. La persona que se muestra a continuación usa un cortacésped. ¿Bajo qué condiciones el cortacésped podría obtener energía de la persona que empuja la podadora? ¿En qué condiciones perdería energía?



12. El trabajo realizado en un sistema le aporta energía. El trabajo realizado por un sistema elimina la energía de él. Da un ejemplo para cada declaración.

13. Dos canicas de masas m y 2 m se dejan caer desde una altura h. Compara sus energías cinéticas cuando llegan al suelo.

14. Compara el trabajo requerido para acelerar un automóvil de masa 2000 kg de 30.0 a 40.0 km/h con el requerido para una aceleración de 50.0 a 60.0 km/h.

15. Supón que estás trotando a velocidad constante. ¿Estás trabajando en el medioambiente y viceversa?

16. Dos fuerzas actúan para duplicar la velocidad de una partícula, moviéndose inicialmente con energía cinética de 1 J. Una de las fuerzas hace 4 J de trabajo. ¿Cuánto trabajo hace la otra fuerza?

7.5 Potencia

17. La mayoría de los electrodomésticos están clasificados en vatios. ¿Esta clasificación depende de cuánto tiempo está encendido el aparato? (Cuando está apagado, es un dispositivo de cero vatios). Explica en términos de la definición de potencia.

18. Explicaa, en términos de la definición de potencia, por qué el consumo de energía a veces se enumera en kilovatios-hora en lugar de julios. ¿Cuál es la relación entre estas dos unidades de energía?

19. Una chispa de electricidad estática, como la que podría recibir de un pomo de la puerta en un día frío y seco, puede llevar algunos cientos de vatios de potencia. Explica por qué no estás herido por una chispa de ese tipo.

20. ¿El trabajo realizado para levantar un objeto depende de qué tan rápido se levanta? ¿La energía consumida depende de qué tan rápido se levante?

21. ¿Puede la potencia gastada por una fuerza ser negativa?

22. ¿Cómo puede una bombilla de 50 W usar más energía que un horno de 1000 W?

Problemas

7.2 Trabajo

23. ¿Cuánto trabajo hace un empleado de caja de supermercado en una lata de sopa que empuja 0.600 m horizontalmente con una fuerza de 5.00 N?

24. Una persona de 75.0 kg sube las escaleras y gana 2.50 m de altura. Encuentra el trabajo realizado para lograr esta tarea.

25. (a) Calcula el trabajo realizado en una cabina de ascensor de 1500 kg por su cable para levantarlo 40.0 m a velocidad constante, suponiendo que la fricción promedia es de 100 N. (b) ¿Cuál es el trabajo realizado en la elevación por la fuerza gravitacional en este proceso? (c) ¿Cuál es el trabajo total realizado en el ascensor?

26. Supón que un automóvil viaja 108 km a una velocidad de 30.0 m/s, y usa 2.0 galones de gasolina. Solo el 30% de la gasolina entra en trabajo útil por la fuerza que mantiene al automóvil en movimiento a velocidad constante a pesar de la fricción. (El contenido de energía de la gasolina es de aproximadamente 140 MJ/gal.) (a) ¿Cuál es la magnitud de la fuerza ejercida para mantener el automóvil en movimiento a velocidad constante? (b) Si la fuerza requerida es directamente proporcional a la velocidad, ¿cuántos galones se usarán para conducir 108 km a una velocidad de 28.0 m/s?

27. Calcula el trabajo realizado por un hombre de 85.0 kg que empuja una caja a 4.00 m hacia arriba a lo largo de una rampa que forma un ángulo de 20.0° con la horizontal (observa la figura). Él ejerce una fuerza de 500 N en la caja paralela a la rampa y se mueve a una velocidad constante. Asegúrate de incluir el trabajo que hace en la caja y en su cuerpo para subir la rampa.



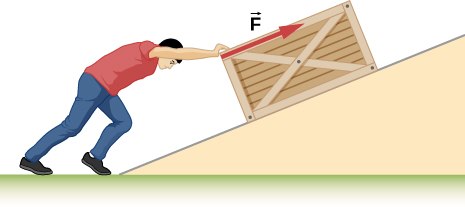
28. ¿Cuánto trabajo hace el muchacho tirando de su hermana 30.0 m en un vagón como se muestra abajo? Supón que la fricción no actúa en el carro.



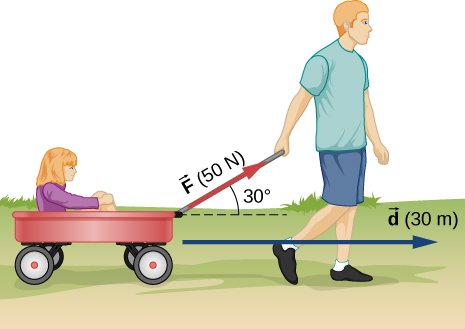
29. Un comprador empuja un carrito de supermercado 20.0 m a velocidad constante en terreno plano, contra una fuerza de fricción de 35.0 N. Empuja en una dirección de 25.0° por debajo de la horizontal. (a) ¿Cuál es el trabajo realizado en el carro por la fricción? (b) ¿Cuál es el trabajo realizado en el carro por la fuerza gravitacional? (c) ¿Cuál es el trabajo realizado en el carro por el comprador? (d) Encuentra la fuerza que ejerce el comprador, usando consideraciones de energía. (e) ¿Cuál es el trabajo total realizado en el carrito?

30. Supón que la patrulla de esquí baja un trineo de rescate y la víctima, que tiene una masa total de 90.0 kg, por una pendiente de 60.0° a velocidad constante, como se muestra a continuación. El coeficiente de fricción entre el trineo y la nieve es 0.100. (a) ¿Cuánto trabajo se realiza por la fricción cuando el trineo se mueve 30,0 m a lo largo de la colina? (b) ¿Cuánto trabajo realiza la cuerda en el trineo en esta distancia? (c) ¿Cuál es el trabajo realizado por la fuerza gravitatoria en el trineo? (d) ¿Cuál es el trabajo total realizado?



31. Una fuerza constante de 20 N empuja una pequeña bola en la dirección de la fuerza sobre una distancia de 5.0 m. ¿Cuál es el trabajo realizado por la fuerza?

32. Un carrito de juguete es tirado una distancia de 6.0 m en línea recta a través del piso. La fuerza que tira del carro tiene una magnitud de 20 N y está dirigida a 37° por encima de la horizontal. ¿Cuál es el trabajo realizado por esta fuerza?

33. Una caja de 5.0 kg descansa sobre una superficie horizontal. El coeficiente de fricción cinética entre la caja y la superficie es μ_K = 0.50. Una fuerza horizontal tira de la caja a velocidad constante durante 10 cm. Encuentra el trabajo realizado por (a) la fuerza horizontal aplicada, (b) la fuerza de fricción y (c) la fuerza neta.

34. Un trineo más el pasajero con una masa total de 50 kg se tiran 20 m por la nieve (μ_k = 0,20) a velocidad constante mediante una fuerza dirigida 25° por encima de la horizontal. Calcula (a) el trabajo de la fuerza aplicada, (b) el trabajo de la fricción, y (c) el trabajo total.

35. Supón que el trineo más el pasajero del problema anterior son empujados 20 m a través de la nieve a velocidad constante con una fuerza dirigida 30° por debajo de la horizontal. Calcula (a) el trabajo de la fuerza aplicada, (b) el trabajo de la fricción, y (c) el trabajo total.

36. ¿Cuánto trabajo hace la fuerza F (x) = (- 2.0/x) N en una partícula a medida que se mueve de x = 2.0 m a x = 5.0 m?

37. ¿Cuánto trabajo se hace contra la fuerza gravitacional en un maletín de 5.0 kg cuando se lleva desde la planta baja hasta el techo del Empire State Building, una subida vertical de 380 m?

38. Se necesitan 500 J de trabajo para comprimir un resorte de 10 cm. ¿Cuál es la fuerza constante del resorte?

39. Una cuerda "bungee" es esencialmente una banda elástica muy larga que puede estirarse hasta cuatro veces su longitud. Sin embargo, su constante de resosrte varía en su estiramiento [ver Menz, P.G. "The Physics of Bungee Jumping". The Physics Teacher (noviembre de 1993) 31: 483-487]. Toma la longitud del cable para que esté a lo largo de la dirección xy define el tramo x como la longitud del cable l menos su longitud no estirada en l₀; es decir, x = l - l₀ (ver figura). Supongamos que una cuerda "bungee" tiene una constante de resorte, para 0 ≤ x ≤ 4.88 m, de k₁ = 204 N/m y para 4.88 m ≤ x, de k₂ = 111 N/m (Recuerda que la constante de resorte es la pendiente de la fuerza F(x) en el tramo x). (a) ¿Cuál es la tensión en la cuerda cuando el estiramiento es de 16.7 m (el máximo deseado para un salto dado)? (b) ¿Cuánto trabajo se debe hacer contra la fuerza elástica de la cuerda "bungee" para estirarla 16,7 m?



40. Una cuerda bungee ejerce una fuerza elástica no lineal de magnitud F(x) = k₁x + k₂x³, donde x es la distancia que se estira la cuerda, k₁ = 204 N/m y k₂ = -0.233 N/m³. ¿Cuánto trabajo se debe hacer en el cable para estirarlo 16,7 m?

41. Los ingenieros desean modelar la magnitud de la fuerza elástica de una cuerda bungee usando la ecuación
F(x) = a[x + 9 m/9m - (9m/x + 9m)²]
donde x es el tramo del cable a lo largo de su longitud y a es una constante. Si se necesitan 22.0 kJ de trabajo para estirar el cable por 16,7 m, determina el valor de la constante a.

42. Una partícula que se mueve en el plano xy está sujeta a una fuerza
F→(x, y) = (50N•m²) (xi^ + yj^)/(x² + y²)x^3/2
donde x e y están en metros. Calcula el trabajo realizado en la partícula por esta fuerza, ya que se mueve en línea recta desde el punto (3 m, 4 m) hasta el punto (8 m, 6 m).

43. Una partícula se mueve a lo largo de una trayectoria curva y(x) = (10m) {1 + cos [(0.1m^-1) x]}, de x = 0 a x = 10 πm, sujeta a una fuerza tangencial de magnitud variable F(x) = (10N) sen[(0.1m^-1)x] . ¿Cuánto trabajo hace la fuerza? (Sugerencia: consulta una tabla de integrales o usa un programa de integración numérica).

7.3 Energía cinética

44. Compara la energía cinética de un camión de 20,000 kg moviéndose a 110 km/h con el de un astronauta de 80.0 kg en órbita moviéndose a 27,500 km/h.

45. (a) ¿Qué tan rápido debe moverse un elefante de 3000 kg para tener la misma energía cinética que un velocista de 65.0 kg corriendo a 10.0 m/s? (b) Discute cómo las energías más grandes necesarias para el movimiento de animales más grandes se relacionarían con las tasas metabólicas.

46. ​​Estima la energía cinética de un portaaviones de 90,000 toneladas que se mueve a una velocidad de 30 nudos. Tendrás que buscar la definición de una milla náutica para convertir la unidad de velocidad, donde 1 nudo equivale a 1 milla náutica por hora.

47. Calcula las energías cinéticas de (a) un automóvil de 2000.0 kg moviéndose a 100.0 km/h; (b) un corredor de 80 kg corriendo a 10 m/s; y (c) un electrón de 9,1 × 10^-31 kg moviéndose a 2,0 × 10⁷ m/s.

48. Un cuerpo de 5.0 kg tiene tres veces la energía cinética de un cuerpo de 8.0 kg. Calcula la relación de las velocidades de estos cuerpos.

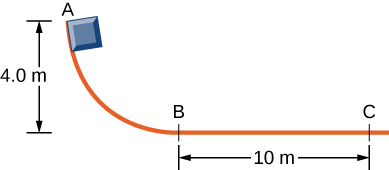
49. Una bala de 8.0 g tiene una velocidad de 800 m/s. (a) ¿Cuál es su energía cinética? (b) ¿Cuál es su energía cinética si la velocidad se reduce a la mitad?

7.4 Teorema del trabajo-energía

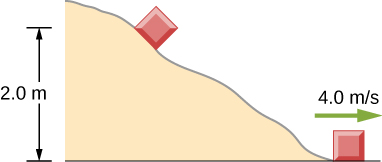
50. (a) Calcula la fuerza necesaria para que un automóvil de 950 kg frene de una velocidad de 90.0 km/h en una distancia de 120 m (una distancia bastante típica para una parada sin pánico). (b) Supongamos que el automóvil golpea un estribo de hormigón a toda velocidad y se detiene en 2,00 m. Calcula la fuerza ejercida sobre el automóvil y compárala con la fuerza que se encuentra en la parte (a).

51. El parachoques de un automóvil está diseñado para soportar una colisión de 4.0 km/h (1.1 m/s) con un objeto inmóvil sin dañar el cuerpo del automóvil. El parachoques amortigua el impacto absorbiendo la fuerza en una distancia. Calcula la magnitud de la fuerza promedio en un parachoques que se derrumba 0.200 m mientras permite el frenado de un automóvil de 900 kg desde una velocidad inicial de 1.1 m/s.

52. Los guantes de boxeo están acolchados para disminuir la fuerza de un golpe. (a) Calcula la fuerza ejercida por un guante de boxeo en la cara de un oponente, si el guante y la cara se comprimen 7.50 cm durante un golpe en el cual el brazo y el guante de 7.00 kg frenan desde una velocidad inicial de 10.0 m/s. (b) Calcula la fuerza ejercida por un golpe idéntico en los antiguos días sangrientos cuando no se usaron guantes, y los nudillos y la cara se comprimirían solo 2,00 cm. Supón que el cambio en la masa al quitar el guante es insignificante. (c) Discute la magnitud de la fuerza con el guante puesto. ¿Parece lo suficientemente alto como para causar daño a pesar de que es más bajo que la fuerza sin guantes?

53. Usando consideraciones de energía, calcula la fuerza promedio que un esprinter de 60.0 kg ejerce hacia atrás en la pista para acelerar de 2.00 a 8.00 m/s en una distancia de 25.0 m, si encuentra un viento en contra que ejerce una fuerza promedio de 30.0 N contra él.

54. Una caja de 5.0 kg tiene una aceleración de 2.0 m/s² cuando es empujada por una fuerza horizontal a través de una superficie con μ_K = 0.50. Encuentra el trabajo realizado a una distancia de 10 cm por (a) la fuerza horizontal, (b) la fuerza de fricción y (c) la fuerza neta. (d) ¿Cuál es el cambio en la energía cinética de la caja?

55. Se aplica una fuerza horizontal constante de 10 N a un carro de 20 kg en reposo en un piso nivelado. Si la fricción es insignificante, ¿cuál es la velocidad del carro cuando se ha empujado a 8,0 m?

56. En el problema anterior, la fuerza de 10 N se aplica en un ángulo de 45° por debajo de la horizontal. ¿Cuál es la velocidad del carro cuando ha sido empujado 8.0 m?

57. Compara el trabajo requerido para detener una caja de 100 kg que se desliza a 1.0 m/s y una bala de 8.0 g que viaja a 500 m/s.

58. Un vagón con su pasajero se ubica en la cima de una colina. Al vagón se le da un ligero empujón y rueda 100 m hacia abajo en una pendiente de 10° hacia la parte inferior de la colina. ¿Cuál es la velocidad del vagón cuando llega al final de la pendiente? Supongamos que la fuerza de retardo de la fricción es insignificante.

59. Una bala de 8.0 g con una velocidad de 800 m/s se dispara en un bloque de madera y penetra 20 cm antes de detenerse. ¿Cuál es la fuerza promedio de la madera en la bala? Supongamos que el bloque no se mueve.

60. Un bloque de 2.0 kg comienza con una velocidad de 10 m/s en la parte inferior de un avión inclinado a 37° con respecto a la horizontal. El coeficiente de fricción de deslizamiento entre el bloque y el avión es μ_k = 0,30. (a) Usa el principio de trabajo-energía para determinar qué tan lejos se desliza el bloque a lo largo del avión antes de detenerse momentáneamente. (b) Después de detenerse, el bloque se desliza hacia abajo del avión. ¿Cuál es su velocidad cuando llega al fondo? (Sugerencia: para el viaje de ida y vuelta, solo la fuerza de fricción funciona en el bloque).

61. Cuando un bloque de 3.0 kg es empujado contra un resorte de fuerza constante de 4.5 × 10³ N/m, el resorte se comprime 8.0 cm. El bloque se libera y se desliza 2,0 m (desde el punto en que se suelta) a través de una superficie horizontal antes de que la fricción lo detenga. ¿Cuál es el coeficiente de fricción cinética entre el bloque y la superficie?

62. Un pequeño bloque de masa 200 g comienza en reposo en A, se desliza hacia B donde su velocidad es v_B = 8.0 m/s, luego se desliza a lo largo de la superficie horizontal una distancia de 10 m antes de detenerse en C. (Ver figura) (a) ¿Cuál es el trabajo de la fricción a lo largo de la superficie curva? (b) ¿Cuál es el coeficiente de fricción cinética a lo largo de la superficie horizontal?



63. Un pequeño objeto se coloca en la parte superior de una pendiente que es esencialmente sin fricción. El objeto se desliza por la pendiente hacia una superficie horizontal áspera, donde se detiene en 5.0 s después de recorrer 60 m. (a) ¿Cuál es la velocidad del objeto en la parte inferior de la pendiente y su aceleración a lo largo de la superficie horizontal? (b) ¿Cuál es la altura de la pendiente?

64. Cuando se suelta, un bloque de 100 g se desliza por el camino que se muestra en la figura, alcanzando el fondo con una velocidad de 4.0 m/s. ¿Cuánto trabajo hace la fuerza de fricción?



65. Una bala de calibre 0.22LR como la mencionada en el Ejemplo 7.10 es disparada a una puerta hecha de un solo espesor de tablas de pino de 1 pulgada. ¿Qué tan rápido viajaría la bala después de que penetrara por la puerta?

66. Un trineo comienza desde el descanso en la parte superior de una pendiente cubierta de nieve que forma un ángulo de 22° con la horizontal. Después de deslizarse 75 m por la pendiente, su velocidad es de 14 m/s. Usa el teorema de trabajo-energía para calcular el coeficiente de fricción cinética entre los corredores del trineo y la superficie nevada.

7.5 Potencia

67. Una persona en buenas condiciones físicas puede emitir 100 W de potencia útil durante varias horas seguidas, tal vez pedaleando un mecanismo que acciona un generador eléctrico. Despreciando cualquier problema de eficiencia del generador y consideraciones prácticas tales como el tiempo de descanso: (a) ¿Cuántas personas se necesitarían para hacer funcionar una secadora eléctrica de 4.00 kW? (b) ¿Cuántas personas se necesitarían para reemplazar una gran planta de energía eléctrica que genera 800 MW?

68. ¿Cuál es el costo de operar un reloj eléctrico de 3.00 W durante un año si el costo de la electricidad es de $ 0.0900 por kW•h?

69. Un acondicionador de aire doméstico grande puede consumir 15,0 kW de potencia. ¿Cuál es el costo de operar este aire acondicionado 3.00 h por día durante 30.0 días si el costo de la electricidad es de $ 0.110 por kW•h?

70. (a) ¿Cuál es el consumo de potencia promedio en vatios de un artefacto que utiliza 5,00 kW•h de energía por día? (b) ¿Cuántos joules de energía consume este aparato en un año?

71. (a) ¿Cuál es la producción de potencia útil promedio de una persona que hace 6.00 × 10⁶J de trabajo útil en 8.00 h? (b) Trabajando a este ritmo, ¿cuánto tiempo le tomará a esta persona levantar 2000 kg de ladrillos a 1,50 m de una plataforma? (El trabajo realizado para levantar su cuerpo se puede omitir porque no se considera útil aquí).

72. Un dragster de 500 kg acelera desde el reposo hasta una velocidad final de 110 m/s en 400 m (aproximadamente un cuarto de milla) y encuentra una fuerza de fricción promedio de 1200 N. ¿Cuál es su potencia promedio en vatios y caballos de fuerza? si esto le lleva 7.30 s?

73. (a) ¿Cuánto tiempo tardará un automóvil de 850 kg con una potencia de salida útil de 40.0 hp (1 hp es igual a 746 W) para alcanzar una velocidad de 15.0 m/s, sin tener en cuenta la fricción? (b) ¿Cuánto tiempo llevará esta aceleración si el automóvil también sube una colina de 3.00 m de altura en el proceso?

74. (a) Encuentra la salida de potencia útil de un motor de un ascensor que levanta una carga de 2500 kg a una altura de 35.0 m en 12.0 s, si también aumenta la velocidad de reposo a 4.00 m/s. Ten en cuenta que la masa total del sistema de contrapeso es de 10.000 kg, de modo que solo se elevan 2500 kg en altura, pero se aceleran los 10.000 kg completos. (b) ¿Cuánto cuesta si la electricidad es de $ 0.0900 por kW•h?

75. a) ¿Cuánto tiempo tardaría un avión de 1,50 × 10⁵ kg con motores que producen 100 MW de potencia para alcanzar una velocidad de 250 m/s y una altitud de 12,0 km si la resistencia del aire fuera insignificante? (b) Si en realidad lleva 900 s, ¿cuál es la potencia? (c) Dada este potencia, ¿cuál es la fuerza promedio de resistencia del aire si el avión tarda 1200 s? (Sugerencia: debes encontrar la distancia que recorre el avión en 1200 s suponiendo una aceleración constante).

76. Calcula la potencia de salida necesaria para que un automóvil de 950 kg suba una pendiente de 2.00° a una velocidad constante de 30.0 m/s mientras encuentra resistencia al viento y fricción que suman 600 N.

77. Un hombre de 80 kg de peso sube por una escalera de 20 m de altura en 10 s. (a) ¿Cuánta energía se usa para levantar al hombre? (b) Si el cuerpo del hombre es 25% eficiente, ¿cuánta energía gasta?

78. El hombre del problema anterior consume aproximadamente 1.05 × 10⁷ J (2500 calorías de comida) de energía por día para mantener un peso constante. ¿Cuál es la potencia promedio que produce durante un día? Compara esto con su producción de energía cuando sube corriendo las escaleras.

79. Un electrón en un tubo de televisión se acelera uniformemente desde el reposo hasta una velocidad de 8,4 × 10⁷ m/s en una distancia de 2,5 cm. ¿Cuál es la potencia entregada al electrón en el instante en que su desplazamiento es de 1.0 cm?

80. El carbón se saca de una mina a una distancia vertical de 50 m por un motor que suministra 500 W a una cinta transportadora. ¿Cuánto carbón por minuto puede traerse a la superficie? Ignora los efectos de la fricción.

81. Una niña tira de su carro de 15 kg por una acera plana aplicando una fuerza de 10 N a 37° con respecto a la horizontal. Supongamos que la fricción es insignificante y que el carro comienza desde el reposo. (a) ¿Cuánto trabajo hace la niña en el carro en los primeros 2.0 s. (b) ¿Cuánta potencia instantánea ejerce ella en t = 2.0s?

82. Un motor de automóvil típico tiene una eficiencia del 25%. Supongamos que el motor de un automóvil de 1000 kg tiene una potencia máxima de 140 hp. ¿Cuál es la pendiente máxima que el automóvil puede subir a 50 km/h si la fuerza de retardo de la fricción es de 300 N?

83. Cuando trota a 13 km/h en una superficie nivelada, un hombre de 70 kg utiliza energía a una velocidad de aproximadamente 850 W. Usando los datos de que el "motor humano" es aproximadamente un 25% eficiente, determina la velocidad a la que este hombre usa energía cuando corre por una pendiente de 5.0° a esta misma velocidad. Supón que la fuerza de retardo de la fricción es la misma en ambos casos.

Problemas adicionales

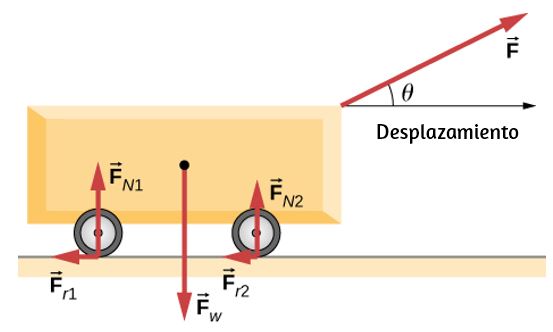
84. Se tira de un carro una distancia D en una superficie horizontal plana mediante una fuerza constante F que actúa en un ángulo θ con la dirección horizontal. Las otras fuerzas sobre el objeto durante este tiempo son la gravedad (F_w), las fuerzas normales (F_N1) y (F_N2), y las fricciones de rodadura F_r1 y F_r2, como se muestra a continuación. ¿Cuál es el trabajo realizado por cada fuerza?



85. Considera una partícula en la que actúan varias fuerzas, una de las cuales se sabe que es constante en el tiempo: F→₁ = (3N)i^ + (4N)j^. Como resultado, la partícula se mueve a lo largo del eje x desde x = 0 hasta x = 5 m en algún intervalo de tiempo. ¿Cuál es el trabajo realizado por F→₁?

86. Considera una partícula en la que actúan varias fuerzas, una de las cuales se sabe que es constante en el tiempo: F→₁ = (3N)i^ + (4N)j^. Como resultado, la partícula se mueve primero a lo largo del eje x desde x = 0 a x = 5m y luego paralela al eje y desde y = 0 a y = 6m. ¿Cuál es el trabajo realizado por F→₁?

87. Considera una partícula en la que actúan varias fuerzas, una de las cuales se sabe que es constante en el tiempo: F→₁ = (3N)i^ + (4N)j^. Como resultado, la partícula se mueve a lo largo de una trayectoria recta desde una coordenada cartesiana de (0 m, 0 m) a (5 m, 6 m). ¿Cuál es el trabajo realizado por F→₁?

88. Considera una partícula en la que actúa una fuerza que depende de la posición de la partícula. Esta fuerza viene dada por F→₁ = (2y)i^ + (3x)j^. Encuentra el trabajo realizado por esta fuerza cuando la partícula se mueve desde el origen hasta un punto de 5 metros a la derecha en el eje x.

89. Un niño tira de un carro de 5 kg con una fuerza de 20 N en un ángulo de 30° sobre la horizontal durante un período de tiempo. Durante este período de tiempo, el carro se mueve una distancia de 12 m en el piso horizontal. (a) Encuentra el trabajo hecho en el carro por el niño. (b) ¿Cuál será el trabajo realizado por el niño si tira con la misma fuerza horizontalmente en lugar de hacerlo en un ángulo de 30° sobre la horizontal en la misma distancia?

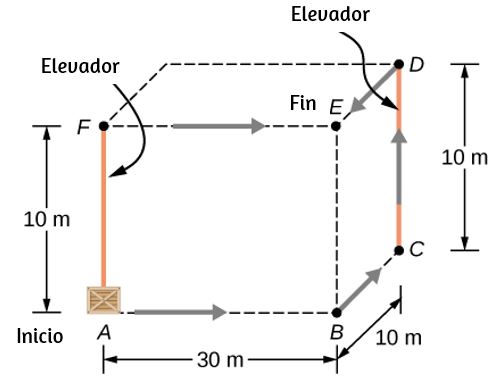
90. Se debe traer una caja de 200 kg de masa de un sitio en la planta baja a un departamento en el tercer piso. Los trabajadores saben que pueden usar el ascensor primero, luego deslizarlo a lo largo del tercer piso hacia el apartamento, o primero deslizar la caja a otra ubicación marcada como C en la figura de abajo, y luego tomar el elevador al tercer piso y deslizarlo sobre el tercer piso una distancia más corta. El problema es que el tercer piso es muy áspero en comparación con la planta baja. Dado que el coeficiente de fricción cinética entre la caja y la planta baja es 0.100 y entre la caja y la superficie del tercer piso es 0.300, encuenta el trabajo que necesitan los trabajadores para cada ruta que se muestra de A a E. Supón que la fuerza de los trabajadores que hay que aplicar es solo lo suficiente para deslizar la caja a velocidad constante (aceleración cero). Nota: El trabajo del elevador contra la fuerza de la gravedad no lo realizan los trabajadores.



91. Un disco de hockey con una masa de 0.17 kg se dispara sobre un suelo áspero con una rugosidad diferente en diferentes lugares, que se puede describir mediante un coeficiente de fricción cinética dependiente de la posición. Para un disco que se mueve a lo largo del eje x, el coeficiente de fricción cinética es la siguiente función de x, donde x está en m: μ(x) = 0.1 + 0.05x. Encuentra el trabajo realizado por la fuerza cinética de fricción en el disco de hockey cuando se ha movido (a) de x = 0 a x = 2 m, y (b) de x = 2 m a x = 4 m.

92. Se requiere una fuerza horizontal de 20 N para mantener una caja de 5.0 kg que viaja a una velocidad constante hacia una pendiente sin fricción para un cambio de altura vertical de 3.0 m. (a) ¿Cuál es el trabajo realizado por la gravedad durante este cambio de altura? (b) ¿Cuál es el trabajo realizado por la fuerza normal? (c) ¿Cuál es el trabajo realizado por la fuerza horizontal?

93. Una caja de 7.0 kg se desliza a lo largo de un piso horizontal sin fricción a 1.7 m/s y choca con un resorte relativamente sin masa que se comprime 23 cm antes de que la caja se detenga. (a) ¿Cuánta energía cinética tiene la caja antes de que colisione con el resorte? (b) Calcule el trabajo realizado por el resorte. (c) Determina la constante de elasticidad del resorte.

94. Estás manejando tu automóvil en una carretera recta con un coeficiente de fricción entre los neumáticos y el camino de 0.55. Un gran pedazo de escombros cae frente a tu vista e inmediatamente aprietas los frenos, dejando una marca de 30.5 m (100 pies) de largo antes de detenerte. Un policía ve tu automóvil parado en la carretera, mira la marca de patín y te da un boleto para viajar por encima del límite de velocidad de 13.4 m/s (30 mph). ¿Deberías luchar contra la multa por exceso de velocidad en la corte?

95. Se está empujando una caja sobre una superficie áspera del piso. Si no se aplica ninguna fuerza sobre la caja, la caja disminuirá la velocidad y se detendrá. Si la caja de 50 kg de masa que se mueve a una velocidad de 8 m/s se detiene en 10 segundos, ¿cuál es la velocidad a la que la fuerza de fricción de la caja retira la energía de la caja?

96. Supón que se requiere una fuerza horizontal de 20 N para mantener una velocidad de 8 m/s de una caja de 50 kg. (a) ¿Cuál es la potencia de esta fuerza? (b) Ten en cuenta que la aceleración de la caja es cero a pesar del hecho de que la fuerza 20 N actúa sobre la caja horizontalmente. ¿Qué le sucede a la energía que se le da a la caja como resultado del trabajo realizado por esta fuerza de 20 N?

97. Los granos de una tolva caen a una velocidad de 10 kg/s verticalmente sobre una cinta transportadora que se mueve horizontalmente a una velocidad constante de 2 m/s. (a) ¿Qué fuerza se necesita para mantener la cinta transportadora en movimiento a la velocidad constante? (b) ¿Cuál es la potencia mínima del motor que impulsa la cinta transportadora?

98. Un ciclista en una carrera debe escalar una colina de 5° de pendiente a una velocidad de 8 m/s. Si la masa de la bicicleta y el ciclista juntos son 80 kg, ¿cuál debe ser la potencia de salida del ciclista para lograr el objetivo?

Problemas reto

99. A continuación se muestra una caja de 40 kg que se empuja a velocidad constante una distancia de 8,0 m a lo largo de una inclinación de 30° por la fuerza horizontal F→. El coeficiente de fricción cinética entre la caja y la inclinación es μ_k = 0.40. Calcula el trabajo realizado por (a) la fuerza aplicada, (b) la fuerza de fricción, (c) la fuerza gravitacional y (d) la fuerza neta.



100. La superficie del problema anterior se modifica de modo que se disminuye el coeficiente de fricción cinética. La misma fuerza horizontal se aplica a la caja, y después de ser empujada a 8,0 m, su velocidad es de 5,0 m/s. ¿Cuánto trabajo ahora se realiza por la fuerza de la fricción? Supongamos que la caja comienza en reposo.

101. La fuerza F(x) varía con la posición, como se muestra a continuación. Encuentra el trabajo realizado por esta fuerza sobre una partícula a medida que se mueve de x = 1.0 m a x = 5.0 m.



102. Encuentra el trabajo hecho por la misma fuerza en el Ejemplo 7.4, entre los mismos puntos, A = (0,0) y B = (2m, 2m), sobre un arco circular de radio 2 m, centrado en (0, 2 m ) Evalúa la integral de la ruta usando coordenadas cartesianas. (Sugerencia: probablemente necesites consultar una tabla de integrales).

103. Responde el problema anterior usando coordenadas polares.

104. Encuentra el trabajo hecho por la misma fuerza en el ejemplo 7.4, entre los mismos puntos, A = (0,0) y B = (2m, 2m), sobre un arco circular de radio 2 m, centrado en (2 m, 0 ) Evalúa la integral de la ruta usando coordenadas cartesianas. (Sugerencia: probablemente necesite consultar una tabla de integrales).

105. Responde el problema anterior usando coordenadas polares.

106. La potencia constante P es entregada a un automóvil de masa m por su motor. Demuestra que si se puede ignorar la resistencia del aire, la distancia recorrida en un tiempo t por el automóvil, comenzando desde el reposo, viene dada por s = (8P/9m)^1/2t^3/2.

107. Supongamos que la resistencia del aire que encuentra un automóvil es independiente de su velocidad. Cuando el automóvil viaja a 15 m/s, su motor entrega 20 hp a sus ruedas. (a) ¿Cuál es la potencia entregada a las ruedas cuando el automóvil viaja a 30 m/s? (b) ¿Cuánta energía usa el automóvil para cubrir 10 km a 15 m/s? ¿A 30 m / s? Supón que el motor es 25% eficiente. (c) Responde las mismas preguntas si la fuerza de la resistencia del aire es proporcional a la velocidad del automóvil. (d) ¿Qué te dicen estos resultados, más tu experiencia con el consumo de gasolina, sobre la resistencia del aire?

108. Considera un resorte lineal, como en la Figura 7.7 (a), con una masa M uniformemente distribuida a lo largo de su longitud. El extremo izquierdo del resorte está fijo, pero el extremo derecho, en la posición de equilibrio x = 0, se mueve con la velocidad v en la dirección x. ¿Cuál es la energía cinética total del resorte? (Sugerencia: Primero expresa la energía cinética de un elemento infinitesimal dm del resorte en términos de la masa total, la longitud de equilibrio, la velocidad del extremo derecho y la posición a lo largo del muelle, luego integre).