Preguntas y problemas - Capítulo VI

Preguntas conceptuales

6.2 Solución de problemas con las leyes de Newton

1. Para simular la aparente ingravidez de la órbita espacial, los astronautas están entrenando en la bodega de un avión de carga que se está acelerando hacia abajo en g. ¿Por qué parecen estar ingrávidos, como se mide al estar de pie en una báscula de baño, en este marco de referencia acelerado? ¿Hay alguna diferencia entre su aparente ingravidez en órbita y en el avión?

6.3 Fricción

2. El pegamento en un pedazo de cinta puede ejercer fuerzas. ¿Pueden estas fuerzas ser un tipo de fricción simple? Explica, considerando especialmente que la cinta puede adherirse a paredes verticales e incluso a techos.

3. Cuando aprendes a conducir, descubres que necesitas dejar un poco el pedal del freno cuando se detiene el automóvil o éste lo haría brúscamente. Explica esto en términos de la relación entre fricción estática y cinética.

4. Cuando empujas un trozo de tiza sobre un pizarrón, a veces chilla porque alterna rápidamente entre deslizarse y pegarse al tablero. Describe este proceso con más detalle, en particular, explicando cómo se relaciona con el hecho de que la fricción cinética es menor que la fricción estática. (El mismo proceso de deslizamiento ocurre cuando los neumáticos chillan en el pavimento).

5. Un especialista en física está cocinando el desayuno cuando nota que la fuerza de fricción entre su espátula de acero y la sartén de teflón es de solo 0.200 N. Al conocer el coeficiente de fricción cinética entre los dos materiales, calcula rápidamente la fuerza normal. ¿Qué es?

6.4 Fuerza centrípeta

6. Si deseas reducir la tensión (que está relacionada con la fuerza centrípeta) en los neumáticos de alta velocidad, ¿utilizarías neumáticos de diámetro grande o pequeño? Explica.

7. Define la fuerza centrípeta. ¿Puede cualquier tipo de fuerza (por ejemplo, tensión, fuerza gravitatoria, fricción, etc.) ser una fuerza centrípeta? ¿Puede cualquier combinación de fuerzas ser una fuerza centrípeta?

8. Si la fuerza centrípeta se dirige hacia el centro, ¿por qué sientes que te "lanzan" lejos del centro cuando un automóvil gira alrededor de una curva? Explica.

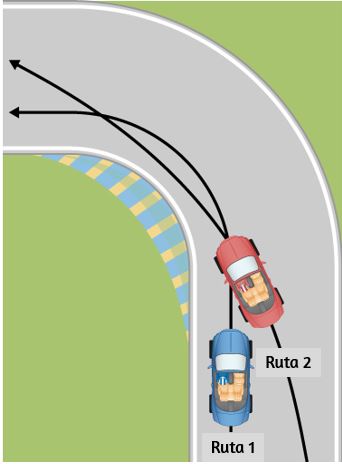
9. Los conductores de autos de carreras rutinariamente cortan esquinas, como se muestra a continuación (Ruta 2). Explica cómo esto permite que la curva se tome a la mayor velocidad.



10. Muchos parques de atracciones tienen juegos que hacen bucles verticales como el que se muestra a continuación. Por seguridad, los carros están sujetos a los rieles de tal manera que no pueden caerse. Si el auto pasa por encima a la velocidad correcta, la gravedad por sí sola suministrará la fuerza centrípeta. ¿Qué otra fuerza actúa y cuál es su dirección si: (a) El automóvil sobrepasa la velocidad más rápido que esta velocidad? (b) ¿El auto pasa por encima a una velocidad más lenta que esta?



11. ¿Qué hace que el agua se elimine de la ropa en una secadora giratoria?

12. Cuando un skater forma un círculo, ¿qué fuerza es la responsable de hacer su giro? Usa un diagrama de cuerpo libre en tu respuesta.

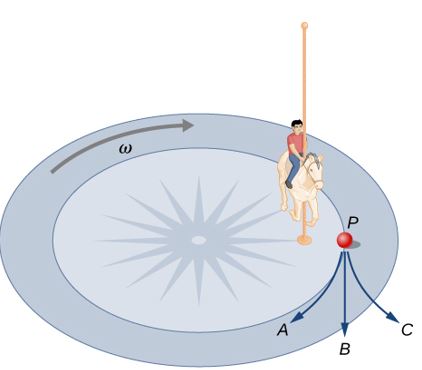
13. Supón que un niño está montando en un tiovivo a una distancia aproximadamente a mitad de camino entre su centro y el borde. El tiene una lonchera apoyada en papel de cera, por lo que hay muy poca fricción entre ella y el tiovivo. ¿Qué camino de los mostrados en la figura tomará la lonchera cuando él la suelte? La lonchera deja un rastro de polvo en el tiovivo. ¿Es ese camino recto, curvado hacia la izquierda o curvado hacia la derecha? Explica tu respuesta.



14. ¿Te sientes arrojado a cada lado cuando trazas una curva idealmente peraltada con la velocidad de tu auto? ¿Cuál es la dirección de la fuerza ejercida sobre ti por el asiento del automóvil?

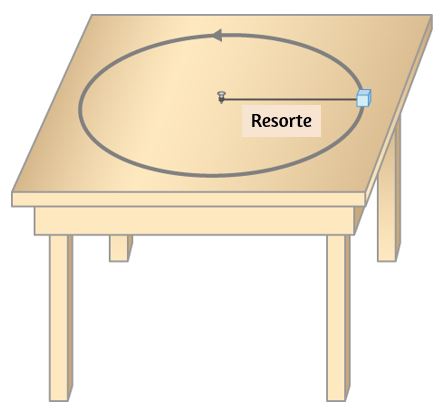
15. Supongamos que una masa se mueve en una trayectoria circular en una mesa sin fricción como se muestra a continuación. En el marco de referencia de la Tierra, no hay fuerza centrífuga que aleje la masa del centro de rotación, sin embargo, hay una fuerza que estira la cuerda uniendo la masa al clavo. Usando conceptos relacionados con la fuerza centrípeta y la tercera ley de Newton, explica qué fuerza estira la cuerda, identificando su origen físico.



16. Cuando se vacía un inodoro o se drena un fregadero, el agua (y otro material) comienza a girar sobre el desagüe en el descenso. Suponiendo que no hay rotación inicial y un flujo inicialmente directamente hacia el desagüe, explica qué causa la rotación y qué dirección tiene en el hemisferio norte. (Ten en cuenta que este es un efecto pequeño y en la mayoría de los inodoros la rotación es causada por chorros de agua direccionales.) ¿Se invertiría la dirección de rotación si se forzara el agua hacia arriba del drenaje?

17. Un automóvil dobla una curva y encuentra un parche de hielo con un coeficiente muy bajo de ficción cinética. El auto se desliza fuera de la carretera. Describe la ruta del automóvil cuando sale de la carretera.

18. En un paseo en un parque de atracciones, unos pasajeros ingresan a un barril vertical grande y se paran contra la pared en su piso horizontal. El barril se centrifuga y el piso se cae. Los pasajeros se sienten como si estuvieran clavados a la pared por una fuerza similar a la fuerza de la gravedad. Esta es una fuerza inercial detectada y utilizada por los pasajeros para explicar los eventos en el marco de referencia giratorio del barril. Explica en un marco inercial de referencia (la Tierra es casi una) lo que atrapa a los pasajeros en la pared e identifica todas las fuerzas que actúan sobre ellos.

19. Dos amigos están teniendo una conversación. Ana dice que un satélite en órbita está en caída libre porque el satélite sigue cayendo hacia la Tierra. Tom dice que un satélite en órbita no está en caída libre porque la aceleración debida a la gravedad no es de 9.80 m/s². ¿Con quién estás de acuerdo y por qué?

20. Un marco de referencia no giratorio situado en el centro del Sol es casi inercial. ¿Por qué no es exactamente un marco de inercia?

6.5 Fuerza de arrastre y velocidad terminal

21. Los atletas como nadadores y ciclistas usan trajes para el cuerpo en la competencia. Formula una lista de pros y contras de tales usos.

22. Se usaron dos expresiones para la fuerza de arrastre experimentada por un objeto en movimiento en un líquido. Uno dependía de la velocidad, mientras que el otro era proporcional al cuadrado de la velocidad. ¿En qué tipos de movimiento sería cada una de estas expresiones más aplicable que la otra?

23. A medida que los automóviles viajan, el petróleo y la gasolina se filtran en la superficie de la carretera. Si cae una ligera lluvia, ¿qué efecto tiene en el control del automóvil? ¿Una lluvia fuerte hace alguna diferencia?

24. ¿Por qué una ardilla puede saltar de la rama de un árbol al suelo y escaparse sin daños, mientras que un humano puede romperse un hueso en una caída de ese tipo?

Problemas

6.2 Solución de problemas con las leyes de Newton

25. Una niña de 30.0 kg en un columpio es empujada hacia un lado y mantenida en reposo por una fuerza horizontal F→ de modo que las cuerdas del columpio están 30.0° con respecto a la vertical. (a) Calcula la tensión en cada una de las dos cuerdas que sostienen el columpio bajo estas condiciones. (b) Calcula la magnitud de F→.

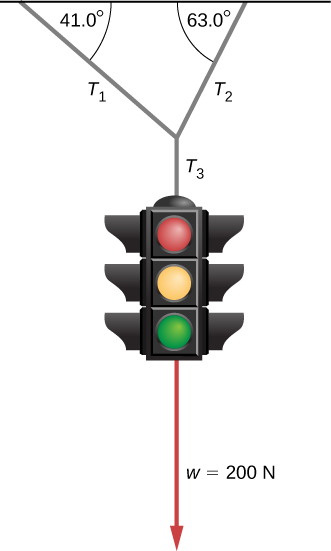
26. Encuentra la tensión en cada uno de los tres cables que sostienen el semáforo si pesa 2.00 × 10² N.



27. Tres fuerzas actúan sobre un objeto, que se considera una partícula, que se mueve con una velocidad constante v = (3i^ - 2j^) m/s. Dos de las fuerzas son F→₁ = (3i^ + 5j^ - 6k^) N y F→₂ = (4i^ - 7j^ + 2k^) N. Encuentra la tercera fuerza.

28. Una pulga salta ejerciendo una fuerza de 1.20 × 10^-5 N directamente hacia abajo en el suelo. Una brisa que sopla sobre la pulga paralela al suelo ejerce una fuerza de 0.500 × 10^-6 N sobre la pulga mientras la pulga aún está en contacto con el suelo. Encuentra la dirección y la magnitud de la aceleración de la pulga si su masa es de 6.00 × 10^-7 kg. No descuides la fuerza gravitatoria.

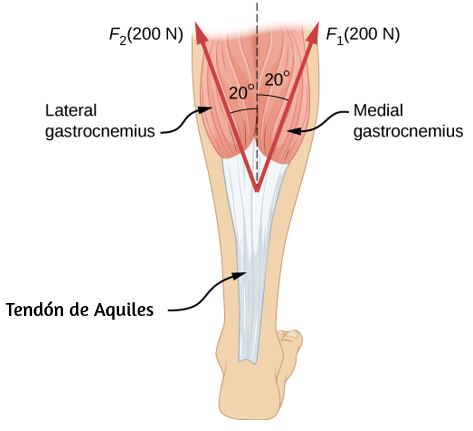
29. Dos músculos en la parte posterior de la pierna tiran hacia arriba del tendón de Aquiles, como se muestra a continuación. (Estos músculos se llaman las cabezas medial y lateral del músculo gastrocnemio). Encuentra la magnitud y la dirección de la fuerza total en el tendón de Aquiles. ¿Qué tipo de movimiento podría ser causado por esta fuerza?



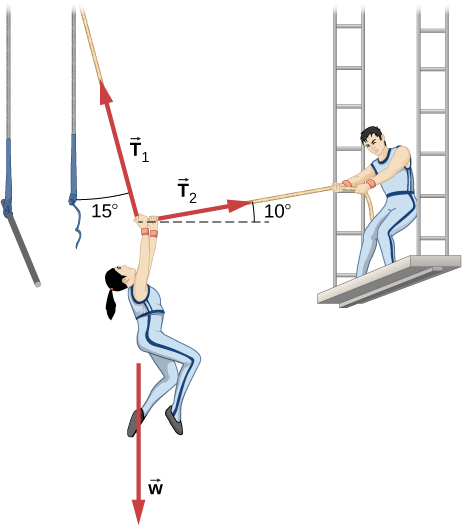
30. Después de un accidente, un artista de circo de 76.0 kg se agarra a un trapecio, que otro artista de circo tira hacia un lado, como se muestra aquí. Calcula la tensión en las dos cuerdas si la persona está momentáneamente inmóvil. Incluye un diagrama de cuerpo libre en su solución.



31. Un delfín de 35.0 kg desacelera de 12.0 a 7.50 m/s en 2.30 s para unirse a otro delfín en juego. ¿Qué fuerza promedio se ejerció para frenar al primer delfín si se movía horizontalmente? (La fuerza gravitacional se equilibra con la fuerza de flotación del agua).

32. Al comenzar una carrera de pie, un esprinter de 70.0 kg ejerce una fuerza promedio de 650 N hacia atrás en el suelo durante 0.800 s. (a) ¿Cuál es su velocidad final? (b) ¿Qué tan lejos viaja?

33. Un cohete grande tiene una masa de 2.00 × 10⁶ kg en el despegue, y sus motores producen un empuje de 3.50 × 10⁷ N. (a) Encuentra su aceleración inicial si despega verticalmente. (b) ¿Cuánto tiempo lleva alcanzar una velocidad de 120 km/h en línea recta, suponiendo masa y empuje constante?

34. Un jugador de baloncesto salta hacia arriba por una pelota. Para hacer esto, baja su cuerpo 0.300 m y luego acelera a través de esta distancia al enderezar con fuerza sus piernas. Este jugador sale del piso con una velocidad vertical suficiente para llevarlo a 0.900 m sobre el piso. (a) Calcula su velocidad cuando abandona el piso. (b) Calcula su aceleración mientras está enderezando sus piernas. Va de cero a la velocidad encontrada en (a) en una distancia de 0.300 m. (c) Calcula la fuerza que ejerce sobre el piso para hacer esto, dado que su masa es de 110.0 kg.

35. Un proyectil de fuegos artificiales de 2,50 kg se dispara directamente desde un mortero y alcanza una altura de 110,0 m. (a) Despreciando la resistencia del aire (una suposición pobre, pero lo haremos para este ejemplo), calcula la velocidad del proyectil cuando sale del mortero. (b) El propio mortero es un tubo de 0.450 m de largo. Calcule la aceleración promedio del proyectil en el tubo a medida que va desde cero hasta la velocidad que se encuentra en (a). (c) ¿Cuál es la fuerza promedio del proyectil en el mortero? Expresa tu respuesta en newtons y como una relación al peso del proyectil.

36. Una papa de 0.500 kg es despedida en un ángulo de 80.0° por encima de la horizontal desde una tubería de PVC utilizada como "pistola de patata" y alcanza una altura de 110.0 m. (a) Despreciando la resistencia del aire, calcula la velocidad de la papa cuando abandone la pistola. (b) El arma en sí es un tubo de 0.450 m de largo. Calcula la aceleración promedio de la papa en el tubo a medida que va desde cero hasta la velocidad que se encuentra en (a). (c) ¿Cuál es la fuerza promedio de la papa en el arma? Exprese tu respuesta en newtons y como una relación con el peso de la patata.

37. Un ascensor lleno de pasajeros tiene una masa de 1.70 × 10³ kg. (a) El elevador acelera hacia arriba desde el reposo a una rata de 1.20 m/s² por 1.50 s. Calcula la tensión en el cable que soporta el elevador. (b) El elevador continúa hacia arriba a velocidad constante durante 8.50 s. ¿Cuál es la tensión en el cable durante este tiempo? (c) El elevador desacelera a una rata de 0.600 m/s² por 3.00 s. ¿Cuál es la tensión en el cable durante la desaceleración? (d) ¿Qué tan alto se ha movido el elevador por encima de su punto de partida original, y cuál es su velocidad final?

38. Una pelota de 20.0 g cuelga del techo de un vagón de carga con una cuerda. Cuando el vagón de carga comienza a moverse, la cuerda forma un ángulo de 35.0° con la vertical. (a) ¿Cuál es la aceleración del vagón de carga? (b) ¿Cuál es la tensión en la cuerda?

39. La mochila de un estudiante, llena de libros de texto, se cuelga de una balanza de resorte unida al techo de un elevador. Cuando el elevador está acelerando hacia abajo a 3.8 m/s², la escala dice 60 N. (a) ¿Cuál es la masa de la mochila? (b) ¿Qué lee la báscula si el elevador se mueve hacia arriba mientras disminuye la velocidad a una rata de 3.8 m/s²? (c) ¿Qué lee la escala si el elevador se mueve hacia arriba a velocidad constante? (d) Si el elevador no tuviera frenos y el cable que lo soporta se soltara para que el elevador pudiera caer libremente, ¿qué leería la balanza de resorte?

40. Un elevador de servicio toma una carga de basura, masa 10.0 kg, desde el piso de un rascacielos en construcción, hasta el nivel del suelo, acelerando hacia abajo a una rata de 1.2 m/s². ¿Encuentra la magnitud de la fuerza que ejerce la basura sobre el piso del elevador de servicio?

41. Un automóvil de una montaña rusa comienza desde el reposo en la parte superior de una pista de 30.0 m de largo e inclinado a 20.0° con respecto a la horizontal. Supongamos que la fricción puede ser ignorada. (a) ¿Cuál es la aceleración del automóvil? (b) ¿Cuánto tiempo transcurre antes de llegar al final de la pista?

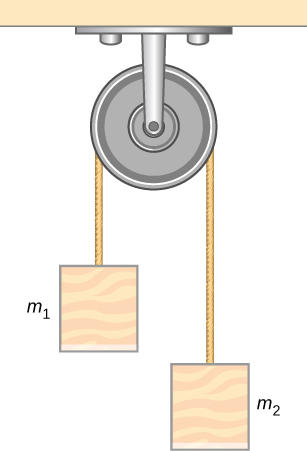
42. El dispositivo que se muestra a continuación es la máquina de Atwood considerada en el Ejemplo 6.5. Suponiendo que las masas de la cuerda y la polea sin fricción son insignificantes, (a) encuentra una ecuación para la aceleración de los dos bloques; (b) encuentra una ecuación para la tensión en la cuerda; y (c) encuentra tanto la aceleración como la tensión cuando el bloque 1 tiene una masa de 2.00 kg y el bloque 2 tiene una masa de 4.00 kg.



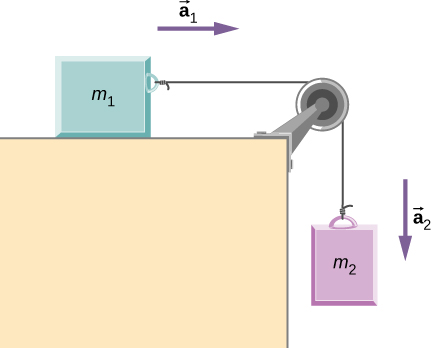
43. Dos bloques están conectados por una cuerda sin masa como se muestra a continuación. La masa del bloque sobre la mesa es de 4.0 kg y la masa colgante es de 1.0 kg. La mesa y la polea son sin fricción. (a) Encuentra la aceleración del sistema. (b) Encuentra la tensión en la cuerda. (c) Encuentra la velocidad con la que la masa colgante golpea el piso si comienza desde el reposo y se ubica inicialmente a 1.0 m del piso.



44. A continuación se muestran dos carros conectados por un cable que pasa sobre una pequeña polea sin fricción. Cada carrito rueda libremente con una fricción insignificante. Calcula la aceleración de los carros y la tensión en el cable.



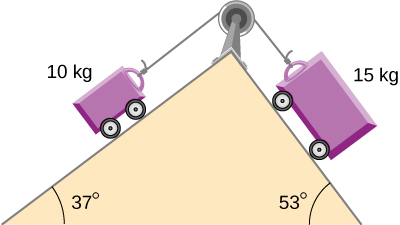
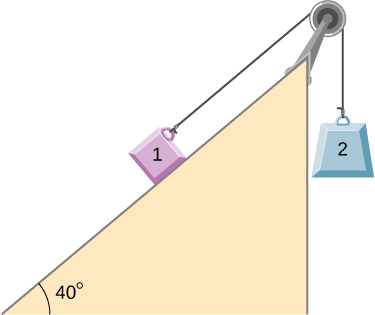
45. Un bloque de 2.00 kg (masa 1) y un bloque de 4.00 kg (masa 2) están conectados por una cuerda ligera como se muestra en la figura; la inclinación de la rampa es 40.0°. La fricción es insignificante. ¿Cuánto es (a) la aceleración de cada bloque y (b) la tensión en la cuerda?

6.3 Fricción

46. ​​(a) Al reconstruir el motor de su automóvil, un físico debe ejercer 3.00 × 10² N de fuerza para insertar un pistón de acero seco en un cilindro de acero. ¿Cuál es la fuerza normal entre el pistón y el cilindro? (b) ¿Qué fuerza tendría que ejercer si las partes de acero fueran engrasadas?

47. (a) ¿Cuál es la fuerza máxima de fricción en la articulación de la rodilla de una persona que soporta 66.0 kg de su masa en esa rodilla? (b) Durante el ejercicio extenuante, es posible ejercer fuerzas en las articulaciones que son fácilmente 10 veces mayores que el peso soportado. ¿Cuál es la fuerza máxima de fricción bajo tales condiciones? Las fuerzas de fricción en las articulaciones son relativamente pequeñas en todas las circunstancias, excepto cuando las articulaciones se deterioran, como por ejemplo por una lesión o artritis. El aumento de las fuerzas de fricción puede causar mayor daño y dolor.

48. Supón que tienes una caja de madera de 120 kg apoyada en un piso de madera, con un coeficiente de fricción estática de 0.500 entre estas superficies de madera. (a) ¿Qué fuerza máxima puedes ejercer horizontalmente en la caja sin moverla? (b) Si continúas ejerciendo esta fuerza una vez que la caja comienza a deslizarse, ¿cuál será entonces su aceleración? Se sabe que el coeficiente de fricción de deslizamiento es 0.300 para esta situación.

49. (a) Si la mitad del peso de un pequeño camión utilitario de 1.00 × 10³ kg es soportado por sus dos ruedas motrices, ¿cuál es la aceleración máxima que puede lograr en concreto seco? (b) ¿Se resbalará un gabinete metálico sobre la cama de madera del camión si acelera a este ritmo? (c) Resuelve ambos problemas suponiendo que el camión tiene tracción en las cuatro ruedas.

50. Un equipo de ocho perros tira de un trineo con correderas de madera encerada sobre nieve húmeda (¡papilla!). Los perros tienen masas promedio de 19.0 kg, y el trineo cargado con su jinete tiene una masa de 210 kg. (a) Calcula la aceleración de los perros comenzando desde el descanso si cada perro ejerce una fuerza promedio de 185 N hacia atrás sobre la nieve. (b) Calcula la fuerza en el acoplamiento entre los perros y el trineo.

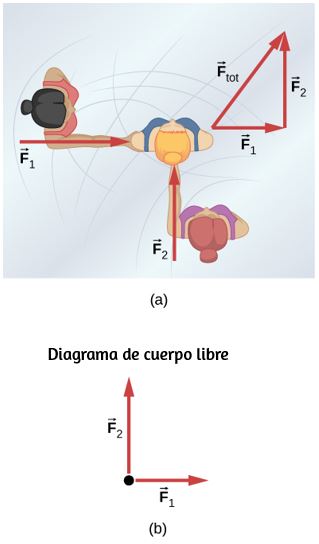
51. Considera que un patinador sobre hielo de 65.0 kg está siendo empujado por los otros dos que se muestran a continuación. (a) Encuentra la dirección y la magnitud de F_tot, la fuerza total ejercida sobre ella por los otros, dado que las magnitudes F₁ y F₂ son 26.4 N y 18.6 N, respectivamente. (b) ¿Cuál es su aceleración inicial si inicialmente está en reposo y usa patines de acero que apuntan en la dirección de F_tot? (c) ¿Cuál es su aceleración suponiendo que ya se está moviendo en la dirección de F_tot? (Recuerda que la fricción siempre actúa en la dirección opuesta a la del movimiento o intento de movimiento entre las superficies en contacto).



52. Demostrar que la aceleración de cualquier objeto por una pendiente sin fricción que forma un ángulo θ con la horizontal es a = gsenθ. (Ten en cuenta que esta aceleración es independiente de la masa).



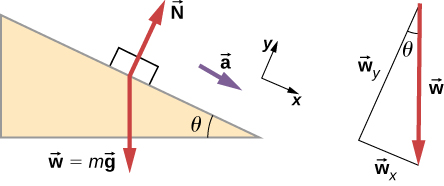
53. Demostrar que la aceleración de cualquier objeto en una pendiente donde la fricción se comporta simplemente (es decir, donde f_k = μ_kN) es a = g(senθ - μ_kcosθ) . Ten en cuenta que la aceleración es independiente de la masa y se reduce a la expresión encontrada en el problema anterior cuando la fricción se vuelve insignificante (μ_k = 0).



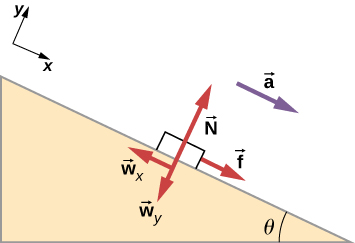
54. Calcula la desaceleración de una tabla nieve que asciende por una pendiente de 5.00°, suponiendo el coeficiente de fricción para la madera encerada sobre nieve húmeda. El resultado del problema anterior puede ser útil, pero ten cuidado de considerar el hecho de que la tabla nieve va cuesta arriba.

55. Una máquina en una oficina de correos envía paquetes por tobogán que baja por una rampa para cargarlos en los vehículos de reparto. (a) Calcula la aceleración de una caja que se dirige hacia abajo en una pendiente de 10.0°, suponiendo que el coeficiente de fricción para un paquete en madera encerada es de 0.100. (b) Encuentra el ángulo de la pendiente hacia abajo para una caja que podría moverse a una velocidad constante. Puedes despreciar la resistencia del aire en ambas partes.

56. Si un objeto debe descansar en una pendiente sin deslizarse, entonces la fricción debe ser igual al componente del peso del objeto paralelo a la inclinación. Esto requiere una mayor fricción para pendientes más pronunciadas. Demuestra que el ángulo máximo de una inclinación por encima de la horizontal para la cual un objeto no se deslizará hacia abajo es θ = tan^-1μ_s. Puedes usar el resultado del problema anterior. Supón que a = 0 y que la fricción estática ha alcanzado su valor máximo.



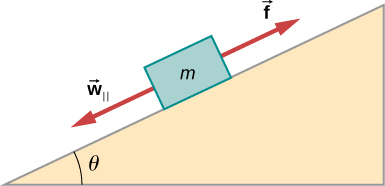
57. Calcula la aceleración máxima de un automóvil que se dirige hacia una pendiente de 6.00° (la que forma un ángulo de 6.00° con la horizontal) en las siguientes condiciones de la carretera. Puedes suponer que el peso del automóvil se distribuye uniformemente en los cuatro neumáticos y que está involucrado el coeficiente de fricción estática, es decir, no se permite que los neumáticos se deslicen durante la desaceleración. Calcula para un automóvil: (a) En concreto seco. (b) En concreto mojado. (c) En hielo, suponiendo que μ_s = 0.100, lo mismo que para los zapatos en hielo.

58. Calcula la aceleración máxima de un automóvil que se dirige hacia una pendiente de 4.00° (la que forma un ángulo de 4.00° con la horizontal) en las siguientes condiciones de la carretera. Supón que solo la mitad del peso del automóvil es soportado por las dos ruedas motrices y que el coeficiente de fricción estática está involucrado, es decir, no se permite que los neumáticos se deslicen durante la aceleración (Ignora si está rodando). (A) En concreto seco. (b) En concreto mojado. (c) En hielo, suponiendo que μ_s = 0.100, lo mismo que para los zapatos en hielo.

59. Repite el problema anterior para un automóvil con tracción en las cuatro ruedas.

60. Un tren de carga consta de dos motores de 8.00 × 10⁵ kg y 45 vagones con masas promedio de 5.50 × 10⁵ kg. (a) Qué fuerza debe ejercer cada motor hacia atrás en la vía para acelerar el tren a una tasa de 5,00 × 10^-2 m/s² si la fuerza de fricción es de 7.50 × 10⁵ N, suponiendo que los motores ejercen fuerzas idénticas? Esta no es una gran fuerza de fricción para un sistema tan masivo. La fricción de rodadura para los trenes es pequeña y, en consecuencia, los trenes son sistemas de transporte muy eficientes desde el punto de vista energético. (b) ¿Cuál es la fuerza en el acoplamiento entre los vagones 37 y 38 (esta es la fuerza que cada uno ejerce sobre el otro), suponiendo que todos los vagones tienen la misma masa y que la fricción se distribuye uniformemente entre todos los autos y motores?

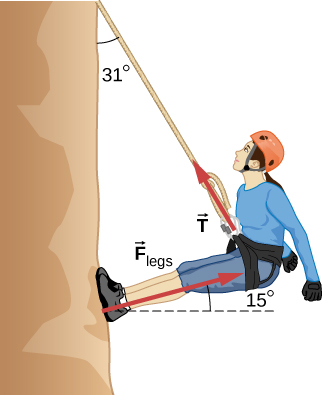
61. Considera el alpinista de 52.0 kg que se muestra a continuación. (a) Encuentra la tensión en la cuerda y la fuerza que el alpinista debe ejercer con los pies sobre la roca vertical para permanecer inmóvil. Supón que la fuerza se ejerce paralela a sus piernas. Además, supón una fuerza insignificante ejercida por sus brazos. (b) ¿Cuál es el coeficiente de fricción mínimo entre sus zapatos y el acantilado?



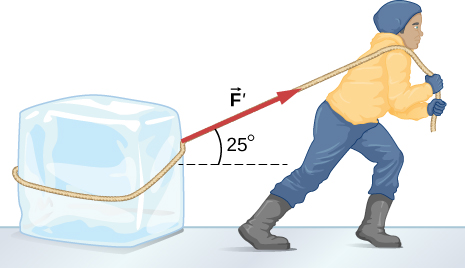
62. Un concursante en un evento deportivo de invierno empuja un bloque de hielo de 45.0 kg a través de un lago congelado como se muestra a continuación. (a) Calcula la fuerza mínima F que debe ejercer para mover el bloque. (b) ¿Cuál es su aceleración una vez que comienza a moverse, si esa fuerza se mantiene?



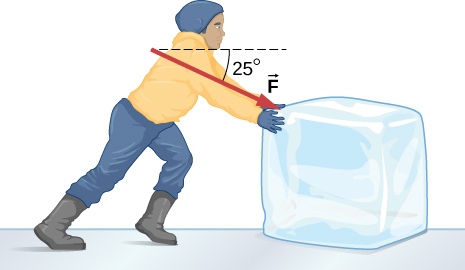
63. El concursante ahora tira del bloque de hielo con una cuerda sobre su hombro en el mismo ángulo sobre la horizontal como se muestra a continuación. Calcula la fuerza mínima F que debe ejercer para mover el bloque. (b) ¿Cuál es su aceleración una vez que comienza a moverse, si esa fuerza se mantiene?



64. En una oficina de correos, un paquete que es una caja de 20.0 kg se desliza por una rampa inclinada a 30.0° con la horizontal. El coeficiente de fricción cinética entre la caja y el plano inclinado es 0.0300. (a) Encuentra la aceleración de la caja. (b) Encuentre la velocidad de la caja cuando llega al final del plano inclinado, si la longitud del plano inclinado es de 2 m y la caja comienza en reposo.

6.4 Fuerza centrípeta

65. (a) Un niño de 22.0 kg está montando un carrusel que gira a 40.0 rev/min. ¿Qué fuerza centrípeta se ejerce si está a 1.25 m de su centro? (b) ¿Qué fuerza centrípeta se ejerce si el tiovivo gira a 3.00 rev/min y está a 8.00 m de su centro? (c) Compara cada fuerza con su peso.

66. Calcula la fuerza centrípeta en el extremo de una pala de turbina eólica de 100 m (radio) que está girando a 0.5 rev/s. Supón que la masa es de 4 kg.

67. ¿Cuál es el ángulo de inclinación ideal para una curva suave de 1.20 km de radio en una carretera con un límite de velocidad de 105 km/h (alrededor de 65 mi/h), suponiendo que todos viajen al límite?

68. ¿Cuál es la velocidad ideal para tomar una curva de 100.0 m de radio, peraltada en un ángulo de 20.0°?

69. (a) ¿Cuál es el radio del giro de un trineo inclinado a 75.0° y tomado a 30.0 m/s, suponiendo que está idealmente inclinado? (b) Calcula la aceleración centrípeta. (c) ¿Esta aceleración te parece grande?

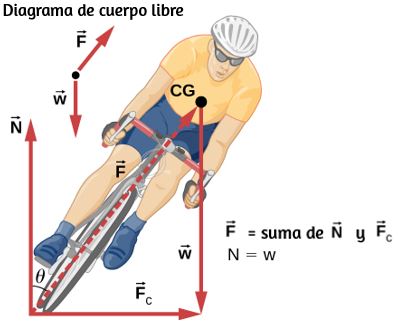
70. Parte de andar en bicicleta implica inclinarse en el ángulo correcto al dar una vuelta, como se ve a continuación. Para ser estable, la fuerza ejercida por el suelo debe estar en una línea que atraviesa el centro de gravedad. La fuerza en la rueda de la bicicleta se puede descomponer en dos componentes perpendiculares: la fricción paralela a la carretera (esto debe suministrar la fuerza centrípeta) y la fuerza normal vertical (que debe ser igual al peso del sistema). (a) Demuestra que θ (como se muestra en la figura) está relacionado con la velocidad v y el radio de curvatura r del giro, de la misma manera que para una carretera con banqueo ideal, es decir, θ = tan^-1(v²/rg). (b) Calcula θ para un giro de 12.0 m/s de radio 30.0 m (como en una carrera).



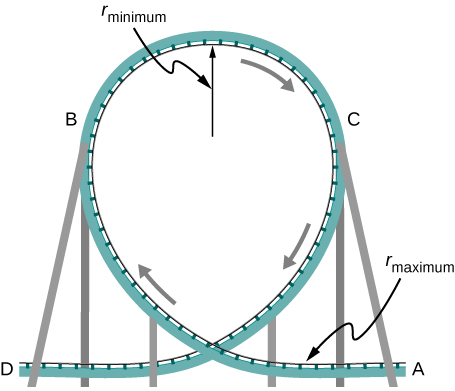
71. Si un automóvil toma una curva inclinada a menos de la velocidad ideal, se necesita fricción para evitar que se deslice hacia el interior de la curva (un problema en las carreteras de montaña heladas). (a) Calcula la velocidad ideal para tomar una curva de 100.0 m de radio acumulada a 15.0°. (b) ¿Cuál es el coeficiente de fricción mínimo necesario para que un conductor asustado tome la misma curva a 20.0 km/h?

72. Las montañas rusas modernas tienen bucles verticales como el que se muestra aquí. El radio de curvatura es más pequeño en la parte superior que en los laterales, por lo que la aceleración centrípeta descendente en la parte superior será mayor que la aceleración debida a la gravedad, manteniendo a los pasajeros firmemente apretados en sus asientos. (a) ¿Cuál es la velocidad de la montaña rusa en la parte superior del circuito si el radio de curvatura es de 15.0 m y la aceleración hacia abajo del carro es de 1.50 g? (b) ¿Cuán alto debe estar de la parte superior del circuito la montaña rusa desde el reposo, suponiendo una fricción insignificante? (c) Si en realidad comienza 5.00 m más alto que tu respuesta en (b), ¿cuánta energía perdió con la fricción? Su masa es de 1.50 × 103kg



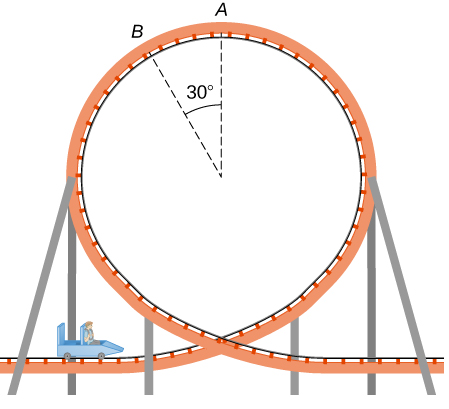
73. Un niño de 40.0 kg de peso se encuentra en un carro de montaña rusa que viaja en un bucle de radio de 7,00 m. En el punto A, la velocidad del carro es de 10.0 m/s, y en el punto B, la velocidad es de 10.5 m/s. Supón que el niño no se sostiene y no usa el cinturón de seguridad. (a) ¿Cuál es la fuerza del asiento del carro para el niño en el punto A? (b) ¿Cuál es la fuerza del asiento del carro para el niño en el punto B? (c) Qué velocidad mínima se requiere para mantener al niño en su asiento en el punto A



74. En el modelo simple de Bohr del estado fundamental del átomo de hidrógeno, el electrón viaja en una órbita circular alrededor de un protón fijo. El radio de la órbita es 5.28 × 10^-11 m, y la velocidad del electrón es 2.18 × 10^-6 m/s. La masa de un electrón es 9.11 × 10^-31 kg. ¿Cuál es la fuerza sobre el electrón?

75. Las vías del ferrocarril siguen una curva circular de radio de 500.0 m y están inclinadas en un ángulo de 5.0°. ¿Para trenes de qué velocidad están diseñadas estas pistas?

76. El acelerador de partículas CERN es circular con una circunferencia de 7,0 km. (a) ¿Cuál es la aceleración de los protones (m = 1.67 × 10^-27kg) que se mueven alrededor del acelerador al 5% de la velocidad de la luz? (La velocidad de la luz es v = 3.00 × 10⁸ m/s) (B) ¿Cuál es la fuerza sobre los protones?

77. Un automóvil redondea una curva no peraltada de radio 65 m. Si el coeficiente de fricción estática entre la carretera y el automóvil es 0.70, ¿cuál es la velocidad máxima a la que el automóvil atraviesa la curva sin deslizarse?

78. Una carretera con peralte está diseñada para el tráfico que se mueve a 90.0 km/h. El radio de la curva es 310 m. ¿Cuál es el ángulo de banca de la carretera?

6.5 Fuerza de arrastre y velocidad terminal

79. La velocidad terminal de una persona que cae en el aire depende del peso y el área de la persona que enfrenta el fluido. Encuentra la velocidad final (en metros por segundo y kilómetros por hora) de un paracaidista de 80.0 kg que cae en una posición de golpe (cabeza) con una superficie de 0.140 m².

80. Dos paracaidistas de 60.0 kg y 90.0 kg salta desde un avión a una altitud de 6.00 × 10³ m, ambos caen en la posición de picada. Haz una suposición sobre sus áreas frontales y calcule sus velocidades terminales. ¿Cuánto tiempo demorará cada paracaidista en llegar al suelo (suponiendo que el tiempo para alcanzar la velocidad terminal es pequeño)? Supón que todos los valores tienen una precisión de tres dígitos significativos.

81. Una ardilla de 560 g con una superficie de 930 cm² cae desde un árbol de 5.0 m hasta el suelo. Estima su velocidad terminal. (Utiliza un coeficiente de arrastre para un paracaidista horizontal). ¿Cuál será la velocidad de una persona de 56 kg que toque el suelo, suponiendo que no se produzca una contribución de arrastre en una distancia tan corta?

82. Para mantener una velocidad constante, la fuerza proporcionada por el motor de un automóvil debe ser igual a la fuerza de arrastre más la fuerza de fricción de la carretera (la resistencia a la rodadura). (a) ¿Cuáles son las fuerzas de arrastre a 70 km/h y 100 km/h para un Toyota Camry? (El área de arrastre es 0.70 m²) (b) ¿Cuál es la fuerza de arrastre a 70 km/h y 100 km/h para un Hummer H2? (El área de arrastre es 2.44 m²). Supón que todos los valores tienen una precisión de tres dígitos significativos.

83. ¿Por qué factor aumenta la fuerza de arrastre en un automóvil a medida que pasa de 65 a 110 km/h?

84. Calcula la velocidad a la que una caída de una gota de lluvia esférica lograría caer de 5,00 km (a) en ausencia de arrastre de aire (b) con arrastre de aire. El tamaño de la gota debe ser de 4 mm, la densidad debe ser de 1,00 × 10³ kg/m y la superficie debe ser πr².

85. Usando la ley de Stokes, verifica que las unidades de viscosidad sean kilogramos por metro por segundo.

86. Encuentra la velocidad terminal de una bacteria esférica (diámetro 2.00 μm) que cae en el agua. Primero deberás observar que la fuerza de arrastre es igual al peso a velocidad terminal. Toma la densidad de la bacteria a 1.10 × 10³ kg/m³.

87. La ley de Stokes describe la sedimentación de partículas en líquidos y puede usarse para medir la viscosidad. Las partículas en líquidos alcanzan la velocidad terminal rápidamente. Uno puede medir el tiempo que le toma a una partícula caer a cierta distancia y luego usar la ley de Stokes para calcular la viscosidad del líquido. Supongamos que un rodamiento de bolas de acero (densidad 7.8 × 10³ kg/m³², (diámetro 3.0 mm) se deja caer en un recipiente con aceite de motor. Tarda 12 s en caer una distancia de 0.60 m. Calcula la viscosidad del aceite.

88. Supongamos que la fuerza resistiva del aire en un paracaidista se puede aproximar mediante f = -bv². Si la velocidad máxima de un paracaidista de 50.0 kg es de 60.0 m/s, ¿cuál es el valor de b?

89. Un pequeño diamante de masa 10.0 g cae del pendiente de un nadador y cae a través del agua, alcanzando una velocidad máxima de 2.0 m/s. (a) Suponiendo que la fuerza de fricción en el diamante obedece a f = -bv, ¿qué es b? (b) ¿Qué tan lejos cae el diamante antes de que alcance el 90 por ciento de su velocidad terminal?

90. (a) ¿Cuál es la velocidad final de un automóvil que viaja originalmente a 50.0 km/h que desacelera a una tasa de 0.400 m s² durante 50.0 s? Supón un coeficiente de fricción de 1.0. (b) ¿Qué no es racional en el resultado? (c) ¿Qué premisa es irracional, o qué premisas son inconsistentes?

91. Una mujer de 75.0 kg se para en una báscula de baño en un ascensor que acelera desde el reposo hasta 30.0 m/s en 2.00 s. (a) Calcula la lectura de la escala en newtons y compárala con su peso. (La escala ejerce una fuerza hacia arriba sobre ella igual a su lectura.) (B) ¿Qué es irracional sobre el resultado? (c) ¿Qué premisa es irracional, o qué premisas son inconsistentes?

92. (a) Calcula el coeficiente de fricción mínimo necesario para que un automóvil ruede sobre una curva de 50.0 m de radio no peraltada a 30.0 m/s. (b) ¿Qué es irracional sobre el resultado? (c) ¿Qué premisas son irrazonables o inconsistentes?

93. Como se muestra a continuación, si M = 5.50 kg, ¿cuál es la tensión en la cuerda 1?



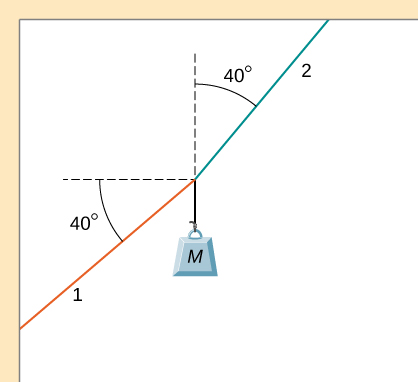
94. Como se muestra a continuación, si F = 60.0 N y M = 4.00 kg, ¿cuál es la magnitud de la aceleración del objeto suspendido? Todas las superficies son sin fricción.



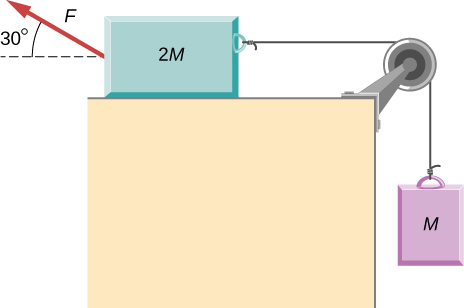
95. Como se muestra a continuación, si M = 6.0kg, ¿cuál es la tensión en la cuerda de conexión? La polea y todas las superficies son sin fricción.



96. Una pequeña sonda de prueba es liberada desde una nave espacial. La sonda espacial tiene una masa de 20.0 kg y contiene 90.0 kg de combustible. Comienza desde el reposo en el espacio profundo, desde el origen de un sistema de coordenadas basado en la nave espacial, y quema combustible a una tasa de 3.00 kg/s. El motor proporciona un empuje constante de 120.0 N. (a) Escribe una expresión para la masa de la sonda espacial en función del tiempo, entre 0 y 30 segundos, suponiendo que el motor enciende el combustible comenzando en t = 0, (b) ¿Cuál es la velocidad después de 15.0 s? (c) ¿Cuál es la posición de la sonda espacial después de 15.0 s, con la posición inicial en el origen? (d) Escribe una expresión para la posición como una función del tiempo, para t> 30.0s.

97. Una bandeja de reciclaje medio lleno tiene una masa de 3.0 kg y se empuja hacia arriba a una inclinación de 40.0° con velocidad constante bajo la acción de una fuerza de 26 N que actúa hacia arriba y es paralela a la inclinación. La inclinación tiene fricción. ¿Qué magnitud de fuerza debe actuar hacia arriba y paralela a la inclinación para que la bandeja se mueva hacia abajo de la pendiente a velocidad constante?

98. Un niño tiene una masa de 6.0 kg y se desliza por una pendiente de 35° con velocidad constante bajo la acción de una fuerza de 34 N que actúa hacia arriba y es paralela a la inclinación. ¿Cuál es el coeficiente de fricción cinética entre el niño y la superficie de la pendiente?

Problemas adicionales

99. Las dos barcazas que se muestran aquí están acopladas por un cable de masa despreciable. La masa de la barcaza delantera es de 2.00 × 10³ kg y la masa de la barcaza trasera es de 3.00 × 10³ kg. Un remolcador tira de la barcaza delantera con una fuerza horizontal de magnitud 20.0 × 10³ N, y las fuerzas de fricción del agua en las barcazas delanteras y traseras son 8.00 × 10³ N y 10.0 × 10³ N, respectivamente. Encuentra la aceleración horizontal de las barcazas y la tensión en el cable de conexión.



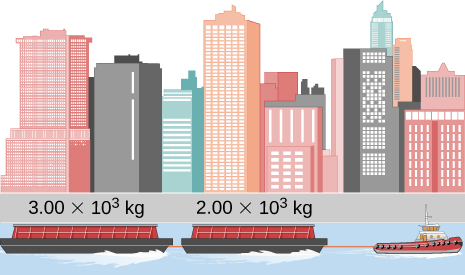
100. Si el orden de las barcazas del ejercicio anterior se invierte para que el remolcador tire de la barcaza de 3.00 × 10³ kg con una fuerza de 20.0 × 103³ N, ¿cuál es la aceleración de la barcazas y la tensión en el cable de acoplamiento?

101. Un objeto con masa m se mueve a lo largo del eje x. Su posición en cualquier momento está dada por x(t) = pt³ + qt² donde p y q son constantes. Encuentra la fuerza neta en este objeto para cualquier momento t.

102. Un helicóptero con una masa de 2.35 × 10⁴ kg tiene una posición dada por r→ (t) = (0.020t³)i^ + (2.2t)j^ - (0.060t²)k^. Encuentra la fuerza neta en el helicóptero en t = 3.0s

103. Situado en el origen, un automóvil eléctrico de masa m está en reposo y en equilibrio. Una fuerza dependiente del tiempo de F→(t) se aplica en el momento t = 0, y sus componentes son F_x(t) = p + nt y F_y(t) = qt donde p, q y n son constantes. Encuentra la posición r→(t) y la velocidad v→(t) como funciones del tiempo t.

104. Una partícula de masa m se encuentra en el origen. Está en reposo y en equilibrio. Una fuerza dependiente del tiempo de F→(t) se aplica en el momento t = 0, y sus componentes son F_x(t) = pt y F_y(t) = n + qt donde p, q y n son constantes. Encuentra la posición r→(t) y la velocidad v→(t) como funciones del tiempo t.

105. Un objeto de 2.0 kg tiene una velocidad de 4.0i^ m/s en t = 0. Una fuerza resultante constante de (2.0i^ + 4.0j^) N actúa sobre el objeto durante 3.0 s. ¿Cuál es la magnitud de la velocidad del objeto al final del intervalo de 3.0 s?

106. Una masa de 1.5 kg tiene una aceleración de (4.0i^ - 3.0j^) m/s². Solo dos fuerzas actúan en la masa. Si una de las fuerzas es (2.0i^ - 1.4j^) N, ¿cuál es la magnitud de la otra fuerza?

107. Se deja caer una caja sobre una cinta transportadora que se mueve a 3,4 m/s. Si el coeficiente de fricción entre la caja y el cinturón es 0.27, ¿cuánto tiempo pasará antes de que la caja se mueva sin deslizarse?

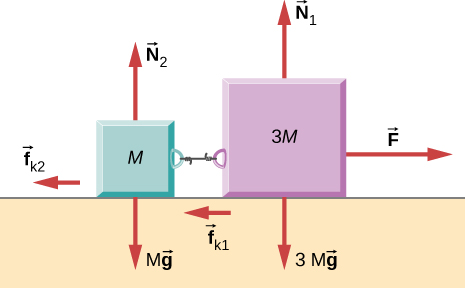
108. A continuación se muestra un bloque de 10.0 kg empujado por una fuerza horizontal F→ de magnitud 200.0 N. El coeficiente de fricción cinética entre las dos superficies es 0.50. Encuentra la aceleración del bloque



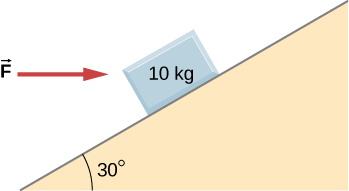
109. Como se muestra a continuación, la masa del bloque 1 es m₁ = 4.0 kg, mientras que la masa del bloque 2 es m₂ = 8.0 kg. El coeficiente de fricción entre m₁ y la superficie inclinada es μ_k = 0.40. ¿Cuál es la aceleración del sistema?



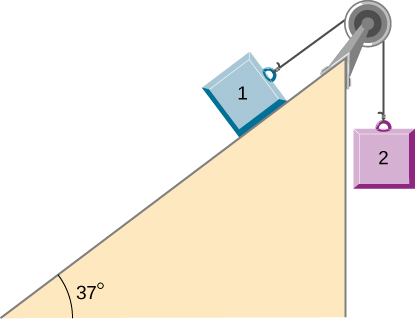
110. Un estudiante está intentando mover un mini refrigerador de 30 kg en su dormitorio. Durante un momento de falta de atención, el mini refrigerador se desliza hacia abajo en una inclinación de 35 grados a velocidad constante cuando aplica una fuerza de 25 N actuando hacia arriba y en paralelo a la inclinación. ¿Cuál es el coeficiente de fricción cinética entre el refrigerador y la superficie de la inclinación?

111. Una caja de masa de 100.0 kg descansa sobre una superficie rugosa inclinada en un ángulo de 37.0° con la horizontal. Una cuerda sin masa a la que se puede aplicar una fuerza paralela a la superficie se une a la caja y la conduce a la parte superior de la inclinación. En su estado actual, la caja está lista para deslizarse y comenzar a moverse hacia abajo. El coeficiente de fricción es 80% del de la caja estática. (a) ¿Cuál es el coeficiente de fricción estática? (b) ¿Cuál es la fuerza máxima que se puede aplicar hacia arriba a lo largo del plano en la cuerda y no mover la caja? (c) Con una fuerza aplicada ligeramente mayor, la caja se deslizará hacia arriba en el plano inclinado. Una vez que comienza a moverse, ¿cuál es su aceleración y qué fuerza es necesaria para mantenerla en movimiento hacia arriba a una velocidad constante? (d) Si a la caja se le da un ligero empujoncito para que comience a descender por el plano, ¿cuál será su aceleración en esa dirección? (e) Una vez que la caja comienza a deslizarse hacia abajo, ¿qué fuerza hacia arriba en la cuerda se requiere para evitar que la caja acelere hacia abajo?

112. Un automóvil se mueve a alta velocidad a lo largo de una carretera cuando el conductor realiza un frenado de emergencia. Las ruedas se bloquean (dejan de rodar) y las marcas de deslizamiento resultantes tienen 32.0 metros de largo. Si el coeficiente de fricción cinética entre los neumáticos y la carretera es 0.550, y la aceleración fue constante durante el frenado, ¿qué tan rápido iba el automóvil cuando las ruedas se bloquearon?

113. Una caja que tiene una masa de 50.0 kg cae horizontalmente de la parte trasera del camión de plataforma, que viaja a 100 km/h. Encuentra el valor del coeficiente de fricción cinética entre la carretera y la caja si la caja se desliza 50 m en la carretera al detenerse. La velocidad inicial de la caja es la misma que la del camión, 100 km/h.



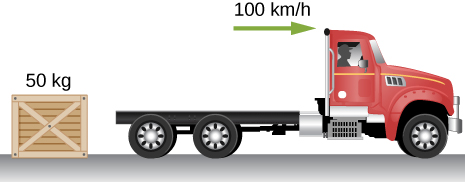
114. Un trineo de 15 kg es tirado a través de una superficie horizontal cubierta de nieve por una fuerza aplicada a una cuerda a 30 grados con la horizontal. El coeficiente de fricción cinética entre el trineo y la nieve es 0.20. (a) Si la fuerza es 33 N, ¿cuál es la aceleración horizontal del trineo? (b) ¿Cuál debe ser la fuerza para tirar del trineo a velocidad constante?

115. Una bola de 30.0 g al final de una cuerda se balancea en un círculo vertical con un radio de 25.0 cm. La velocidad de rotación es 200.0 cm/s. Encuentra la tensión en la cuerda: (a) en la parte superior del círculo, (b) en la parte inferior del círculo y (c) a una distancia de 12.5 cm del centro del círculo (r = 12.5 cm).

116. Una partícula de masa de 0.50 kg comienza a moverse a través de una trayectoria circular en el plano xy con una posición dada por r→(t) = (4.0cos3t)i^ + (4.0sen3t)j^ donde r está en metros y t es en segundos. (a) Encuentra los vectores de velocidad y aceleración como funciones del tiempo. (b) Muestra que el vector de aceleración siempre apunta hacia el centro del círculo (y por lo tanto representa la aceleración centrípeta). (c) Encuentra el vector de fuerza centrípeta como una función del tiempo.

117. Un ciclista de acrobacias monta en el interior de un cilindro de 12 m de radio. El coeficiente de fricción estática entre los neumáticos y la pared es de 0.68. Encuentra el valor de la velocidad mínima para que el ciclista realice el truco.

118. Cuando un cuerpo de masa 0,25 kg se une a un resorte vertical sin masa, se extiende 5,0 cm desde su longitud no estirada de 4,0 cm. El cuerpo y el resorte se colocan sobre una superficie horizontal sin fricción y se rotan alrededor del extremo sujetado del resorte a 2,0 rev/s. ¿Qué tan lejos se estira el resorte?

119. Las vías férreas siguen una curva circular de radio de 500.0 m y están inclinadas en un ángulo de 5.00°. ¿Para trenes de qué velocidad están diseñadas estas vías?

120. Una plomada cuelga del techo de un vagón de ferrocarril. El automóvil redondea una pista circular de radio 300.0 m a una velocidad de 90.0 km/h. ¿En qué ángulo relativo a la vertical cuelga la plomada?

121. Un avión vuela a 120.0 m/s y los bancos a un ángulo de 30°. Si su masa es de 2.50 × 10³ kg, (a) ¿cuál es la magnitud de la fuerza de elevación? (b) ¿cuál es el radio del giro?

122. La posición de una partícula está dada por r→ (t) = A (cosωti^ + senωtj^), donde ω es una constante. (a) Demuestra que la partícula se mueve en un círculo de radio A. (b) Calcule dr→/dt y luego demuestra que la velocidad de la partícula es una constante Aω. (c) Determina d²r→/dt² y demuestra que a está dada por a_c = rω². (d) Calcula la fuerza centrípeta en la partícula. [Sugerencia: para (b) y (c), necesitarás usar (d/dt)(cosωt) = - ωsenωt y (d/dt) (senωt) = ωcosωt .

123. Dos bloques conectados por una cuerda se arrastran a través de una superficie horizontal mediante una fuerza aplicada a uno de los bloques, como se muestra a continuación. El coeficiente de fricción cinética entre los bloques y la superficie es 0.25. Si cada bloque tiene una aceleración de 2.0 m/s² hacia la derecha, ¿cuál es la magnitud F de la fuerza aplicada?



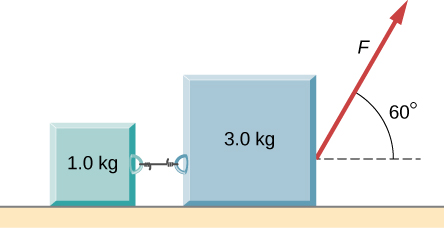
124. Como se muestra a continuación, el coeficiente de fricción cinética entre la superficie y el bloque más grande es 0.20, y el coeficiente de fricción cinética entre la superficie y el bloque más pequeño es 0.30. Si F = 10 N y M = 1.0 kg, ¿cuál es la tensión en la cuerda de conexión?



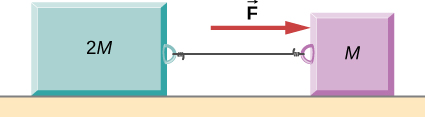
125. En la figura, el coeficiente de fricción cinética entre la superficie y los bloques es μ_k. Si M = 1.0 kg, encuentra una expresión para la magnitud de la aceleración de cualquiera de los bloques (en términos de F, μ_k, y g).



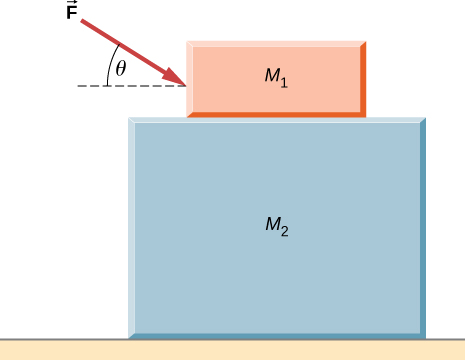
126. Dos bloques se apilan como se muestra a continuación, y se apoyan en una superficie sin fricción. Hay fricción entre los dos bloques (coeficiente de fricción μ). Se aplica una fuerza externa al bloque superior en un ángulo θ con la horizontal. ¿Cuál es la fuerza máxima F que se puede aplicar para que los dos bloques se muevan juntos?



127. Una caja descansa en la parte posterior (horizontal) de un camión. El coeficiente de fricción estática entre la caja y la superficie sobre la que descansa es 0.24. ¿Qué distancia máxima puede recorrer el camión (comenzando desde el reposo y moviéndose horizontalmente con aceleración constante) en 3.0 s sin tener que deslizar la caja?

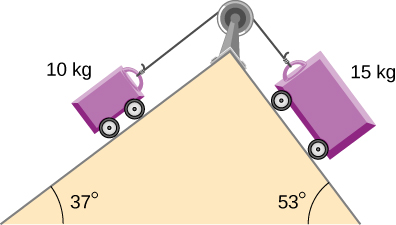
128. Abajo se muestra un plano de doble inclinación. El coeficiente de fricción en la superficie izquierda es 0.30, y en la superficie derecha 0.16. Calcule la aceleración del sistema.

Problemas reto

129. En un capítulo posterior, encontrarás que el peso de una partícula varía con la altitud de manera que w = mgr₀²/r²w r₀ es el radio de la Tierra y r es la distancia desde el centro de la Tierra. Si la partícula se dispara verticalmente con la velocidad v₀ de la superficie de la Tierra, determina su velocidad como una función de la posición r. (Sugerencia: usa adr = vdv, ala reorganización mencionada en el texto).

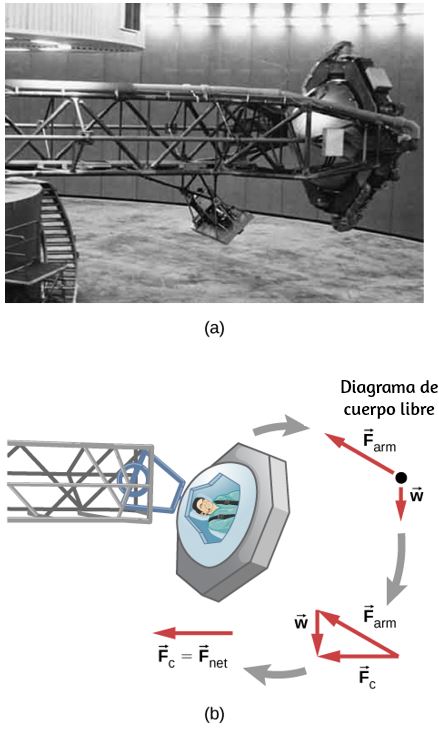
130. Una centrifugadora grande, como la que se muestra a continuación, se utiliza para exponer a los aspirantes a astronautas a aceleraciones similares a las experimentadas en los lanzamientos de cohetes y las reentradas atmosféricas. (a) ¿A qué velocidad angular está la aceleración centrípeta 10g si el aspirante está a 15.0 m del centro de rotación? (b) La jaula del aspirante cuelga de un pivote en el extremo del brazo, lo que le permite oscilar hacia afuera durante la rotación como se muestra en la figura inferior que lo acompaña. ¿En qué ángulo θ debajo de la horizontal colgará la jaula cuando la aceleración centrípeta sea 10g? (Sugerencia: el brazo suministra fuerza centrípeta y soporta el peso de la jaula. Dibuja un diagrama de cuerpo libre de las fuerzas para ver cuál debe ser el ángulo θ).



131. Un automóvil de masa 1000.0 kg viaja a lo largo de una carretera nivelada a 100.0 km/h cuando se aplican los frenos. Calcula la distancia de frenado si el coeficiente de fricción cinética de los neumáticos es 0.500. Desprecia la resistencia del aire. (Sugerencia: dado que la distancia recorrida es de interés más que el tiempo, x es la variable independiente deseada y no t. Usa la regla de la cadena para cambiar la variable: dv/dt = dv/dxdx/dt = vdv/dx

132. Un avión que vuela a 200.0 m/s hace un giro que demora 4.0 min. ¿Qué ángulo de inclinación se requiere? ¿Cuál es el porcentaje de incremento en el peso percibido por los pasajeros?

133. Un paracaidista se encuentra a una altitud de 1520 m. Después de 10.0 segundos de caída libre, abre su paracaídas y encuentra que la resistencia del aire, F_D, viene dada por la fórmula F_D = -bv, donde b es una constante y v es la velocidad. Si b = 0.750, y la masa del paracaidista es 82.0 kg, primero establece ecuaciones diferenciales para la velocidad y la posición, y luego encuentra: (a) la velocidad del paracaidista cuando se abre el paracaídas, (b) la distancia de caída antes de que se abra el paracaídas, (c) la velocidad terminal después de que se abre el paracaídas (encontrar la velocidad límite), y (d) el tiempo que el paracaidista está en el aire después de que se abre el paracaídas.

134. En un comercial de televisión, se suelta una pequeña cuenta esférica de masa 4,00 g desde el reposo en t = 0 en una botella de champú líquido. La velocidad terminal se observa que es de 2.00 cm/s. Encuentra (a) el valor de la constante b en la ecuación v = mg/b (1 - e^-bt/m), y (b) el valor de la fuerza resistiva cuando la cuenta esférica alcanza la velocidad terminal.

135. Un navegante y un barco a motor descansan en un lago. Juntos, tienen una masa de 200.0 kg. Si el empuje del motor es una fuerza constante de 40.0 N en la dirección del movimiento, y si la fuerza de resistencia del agua es numéricamente equivalente a 2 veces la velocidad v del bote, configura y resuelve la ecuación diferencial para encontrar: (a) la velocidad del barco en el tiempo t; (b) la velocidad límite .