Preguntas y problemas - Capítulo V

Preguntas conceptuales

5.2 Fuerzas

1. ¿Qué propiedades tienen las fuerzas que nos permiten clasificarlas como vectores?

5.3 Primera Ley de Newton: Ley de inercia

2. Tomando un marco ligado a la Tierra como inercial, ¿cuál de los siguientes objetos no puede tener marcos inerciales unidos a ellos, y cuáles son marcos de referencia inerciales? (a) Un automóvil que se mueve a velocidad constante (b) Un automóvil que se está acelerando (c) Un ascensor en caída libre (d) Una cápsula espacial que orbita la Tierra (e) Un elevador que desciende uniformemente

3. Una mujer estaba transportando una caja abierta de tortas a una fiesta escolar. El auto frente a ella se detuvo de repente; ella aplicó sus frenos de inmediato. Ella estaba usando su cinturón de seguridad y no sufrió ningún daño físico (simplemente una gran cantidad de vergüenza), pero las tortas volaron al tablero y se convirtió en una "pasta de tortas". Explique lo que sucedió.

5.4 Segunda Ley de Newton

4. ¿Por qué podemos despreciar fuerzas como las que mantienen un cuerpo unido cuando aplicamos la segunda ley de Newton?

5. Una roca es arrojada hacia arriba. En la parte superior de la trayectoria, la velocidad es momentáneamente cero. ¿Esto implica que la fuerza que actúa sobre el objeto es cero? Explica tu respuesta.

5.5 Masa y peso

6. ¿Cuál es la relación entre el peso y la masa? ¿Cuál es una propiedad intrínseca e inmutable de un cuerpo?

7. ¿Cuánto pesa un astronauta de 70 kg en el espacio, lejos de cualquier cuerpo celeste? ¿Cuál es su masa en este lugar?

8. ¿Cuál de las siguientes afirmaciones es correcta? (a) La masa y el peso son la misma cosa expresada en diferentes unidades. (b) Si un objeto no tiene peso, no debe tener masa. (c) Si el peso de un objeto varía, también lo debe ser la masa. (d) La masa y la inercia son conceptos diferentes. (e) El peso es siempre proporcional a la masa.

9. Cuando te paras en la Tierra, tus pies presionan contra ella con una fuerza igual a tu peso. ¿Por qué la Tierra no se aleja de ti?

10. ¿Cómo darías el valor de g→ en forma de vector?

5.6 La tercera Ley de Newton

11. Identifica las fuerzas de acción y reacción en las siguientes situaciones: (a) la Tierra atrae a la Luna, (b) un niño patea una pelota de fútbol americano, (c) un cohete acelera hacia arriba, (d) un automóvil acelera hacia adelante, (e) un atleta salta, y (f) una bala es disparada desde un arma.

12. Supón que estás sosteniendo una taza de café en la mano. Identifica todas las fuerzas en la taza y la reacción a cada fuerza.

13. a) ¿Por qué retrocede un rifle ordinario (retroceso) cuando se dispara? (b) El cañón de un rifle sin retroceso está abierto en ambos extremos. Describe cómo se aplica la tercera ley de Newton cuando uno es despedido. (c) ¿Puedes mantenerte cerca de uno de manera segura cuando se dispara?

5.7 Fuerzas comunes

14. Se coloca una mesa sobre una alfombra. Luego se coloca un libro sobre la mesa. ¿Sobre qué ejerce el piso una fuerza normal?

15. Una partícula se mueve hacia la derecha. (a) ¿Puede una fuerza sobre ella actuar hacia la izquierda? Si es así, ¿qué pasaría? (b) ¿Puede esa fuerza actuar hacia abajo? ¿Si es así por qué?

5.8 Dibujando diagramas de cuerpo libre

16. Al completar la solución para un problema que involucra fuerzas, ¿qué hacemos después de construir el diagrama de cuerpo libre? Es decir, ¿qué aplicamos?

17. Si un libro está ubicado en una mesa, ¿cuántas fuerzas se deben mostrar en un diagrama de cuerpo libre del libro? Describelas.

18. Si el libro en la pregunta anterior está en caída libre, ¿cuántas fuerzas se deben mostrar en un diagrama de cuerpo libre del libro? Describelas.

Problemas

5.2 Fuerzas

19. Dos cuerdas están unidas a un árbol, y las fuerzas de F→₁ = 2.0i^ + 4.0j^ N y F→₂ = 3.0i^ + 6.0j^ N se aplican. Las fuerzas son coplanarias (en el mismo plano). (a) ¿Cuál es la resultante (fuerza neta) de estos dos vectores de fuerza? (b) Encuentra la magnitud y dirección de esta fuerza neta.

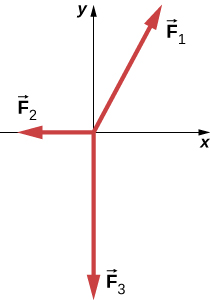
20. Un poste telefónico tiene tres cables tirando como se muestra en la figura, con F→₁ = (300.0i^ + 500.0j^), F→₂ = -200.0i^ , y F→₃ = -800.0j^. (a) Encuentra la fuerza neta en el poste telefónico en forma de componentes. (b) Encuentra la magnitud y dirección de esta fuerza neta



21. Dos adolescentes están tirando de cuerdas atadas a un árbol. El ángulo entre las cuerdas es 30.0°. David tira con una fuerza de 400.0 N y Stephanie tira con una fuerza de 300.0 N. (a) Encuentra en forma de componentes la fuerza neta. (b) Encuentre la magnitud de la fuerza (neta) resultante en el árbol y el ángulo que forma con la cuerda de David.

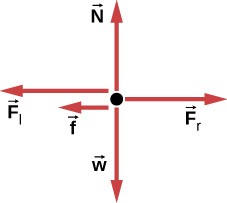
5.3 Primera Ley de Newton: Ley de inercia

22. Dos fuerzas de F→₁ = 75.02/√2/(i^ - j^) N y F→₂ = 150.0/√2/(i^ - j^) N actúa sobre un objeto. Encuentra la tercera fuerza F→₃ que se necesita para equilibrar las dos primeras fuerzas.

23. Mientras se desliza un sofá por el suelo, Andrea y Jennifer ejercen fuerzas F→_A y F→_J en el sofá. La fuerza de Andrea se dirige al norte con una magnitud de 130.0 N y la fuerza de Jennifer es 32° al noreste con una magnitud de 180.0 N. (a) Encuentra la fuerza neta en componentes rectangulares. (b) Encuentra la magnitud y dirección de la fuerza neta. (c) Si los compañeros de piso de Andrea y Jennifer, David y Stephanie, no están de acuerdo con la mudanza y quieren evitar su reubicación, ¿con qué fuerza combinada F→_DS deben empujar para que el sofá no se mueva?

5.4 Segunda Ley de Newton

24. Andrea, una velocista de 63.0 kg, comienza una carrera con una aceleración de 4.200 m/s². ¿Cuál es la fuerza externa neta sobre ella?

25. Si el velocista del problema anterior acelera a esa velocidad durante 20.00 m y luego mantiene esa velocidad durante el resto de una carrera de 100.00 m, ¿cuál será su tiempo para la carrera?

26. Un limpiador empuja un carrito de lavandería de 4.50 kg de tal manera que la fuerza externa neta sobre él sea de 60.0 N. Calcule la magnitud de la aceleración de su carrito.

27. Los astronautas en órbita aparentemente carecen de peso. Esto significa que se necesita un método inteligente para medir la masa de astronautas para controlar sus ganancias o pérdidas de masa y ajustar su dieta. Una forma de hacerlo es ejercer una fuerza conocida sobre un astronauta y medir la aceleración producida. Supongamos que se ejerce una fuerza externa neta de 50.0 N, y la aceleración de un astronauta se mide en 0.893 m/s². (a) Calcula su masa. (b) Al ejercer una fuerza sobre el astronauta, el vehículo en el que ella orbita experimenta una fuerza igual y opuesta. Utiliza este conocimiento para encontrar una ecuación para la aceleración del sistema (astronauta y nave espacial) que un observador cercano pueda medir. (c) Discute cómo esto afectaría la medición de la aceleración del astronauta. Propón un método por el cual se evita el retroceso del vehículo.

28. En la Figura 5.12, la fuerza externa neta en el cortacésped de 24 kg se da como 51 N. Si la fuerza de fricción que se opone al movimiento es 24 N, ¿qué fuerza F (en newtons) está ejerciendo la persona sobre el cortacésped? Supongamos que el cortacésped se mueve a 1,5 m/s cuando se elimina la fuerza F. ¿Qué distancia recorrerá el cortacésped antes de detenerse?

29. El trineo cohete que se muestra a continuación desacelera a una velocidad de 196 m/s². ¿Qué fuerza es necesaria para producir esta desaceleración? Supongamos que los cohetes están apagados. La masa del sistema es 2.10 × 10³ kg.



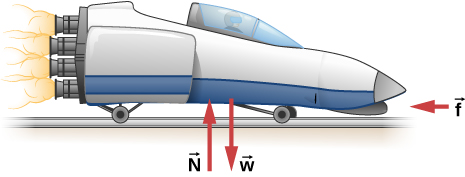
30. Si el trineo que se muestra en el problema anterior comienza con solo un cohete ardiendo, ¿cuál es la magnitud de esta aceleración? Suponga que la masa del sistema es 2.10 × 10³ kg, el empuje T es 2.40 × 10⁴ N, y la fuerza de fricción que se opone al movimiento es 650.0 N. (b) ¿Por qué la aceleración no es un cuarto de lo que es con todos los cohetes ardiendo?

31. ¿Cuál es la desaceleración del trineo si se detiene en 1.10 s desde una velocidad de 1000.0 km/h? (Tal desaceleración causó que un sujeto de prueba se desmayara y tenga ceguera temporal).

32. Suponga que dos niños empujan horizontalmente, pero en direcciones exactamente opuestas, hacia un tercer niño en un vagón. El primer niño ejerce una fuerza de 75.0 N, el segundo ejerce una fuerza de 90.0 N, la fricción es de 12.0 N, y la masa del tercer niño más el carro es de 23.0 kg. (a) ¿Cuál es el sistema de interés si se va a calcular la aceleración del niño en el vagón? (Ver el diagrama de cuerpo libre.) (B) Calcula la aceleración. (c) ¿Cuál sería la aceleración si la fricción fuera 15.0 N?



33. Una motocicleta potente puede producir una aceleración de 3.50 m/s² mientras viaja a 90.0 km/h. A esa velocidad, las fuerzas que resisten el movimiento, incluida la fricción y la resistencia del aire, totalizan 400.0 N. (La resistencia del aire es análoga a la fricción del aire. Siempre se opone al movimiento de un objeto.) ¿Cuál es la magnitud de la fuerza que la motocicleta ejerce hacia atrás en el suelo para producir su aceleración, si la masa de la motocicleta con el jinete es de 245 kg?

34. Un automóvil con una masa de 1000.0 kg acelera de 0 a 90.0 km/h en 10.0 s. (a) ¿Cuál es su aceleración? (b) ¿Cuál es la fuerza neta en el automóvil?

35. El conductor en el problema anterior aplica los frenos cuando el automóvil se mueve a 90.0 km/h, y el automóvil se detiene después de viajar 40.0 m. ¿Cuál es la fuerza neta en el automóvil durante su desaceleración?

36. Un pasajero de 80.0 kg viaja en un SUV a 1.00 × 10³ km/h y lleva puesto el cinturón de seguridad. El conductor golpea los frenos y el SUV se detiene en 45.0 m. Encuentra la fuerza del cinturón de seguridad en el pasajero.

37. Una partícula de masa de 2,0 kg es actuada por una única fuerza F→₁ = 18i^ N. (a) ¿Cuál es la aceleración de la partícula? (b) Si la partícula comienza en reposo, ¿qué distancia recorre en los primeros 5.0 s?

38. Supongamos que la partícula del problema anterior también experimenta fuerzas F→₂ = -15i^ N y F→₃ = 6.0j^ N. ¿Cuál es su aceleración en este caso?

39. Encuentre la aceleración del cuerpo de masa 5.0 kg que se muestra a continuación:



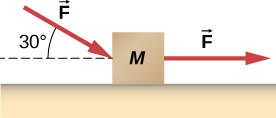
40. En la siguiente figura, la superficie horizontal sobre la que se desliza este bloque no tiene fricción. Si las dos fuerzas que actúan sobre él tienen una magnitud F = 30.0 N y M = 10.0kg, ¿cuál es la magnitud de la aceleración resultante del bloque?

5.5 Masa y peso

41. El peso de un astronauta más su traje espacial en la Luna es de solo 250 N. (a) ¿Cuánto pesa el astronauta en la Tierra? (b) ¿Cuál es la masa en la Luna? ¿En la tierra?

42. Supongamos que la masa de un módulo totalmente cargado en el que los astronautas despegan de la Luna es de 1,00 × 10⁴ kg. El empuje de sus motores es 3.00 × 10⁴ N. (a) Calcula la magnitud de aceleración del módulo en un despegue vertical desde la Luna. (b) ¿Podría despegar de la Tierra? ¿Si no, porque no? Si pudieras, calcula la magnitud de su aceleración.

43. Un trineo cohete acelera a una velocidad de 49.0 m/s². Su pasajero tiene una masa de 75.0 kg. (a) Calcula la componente horizontal de la fuerza que ejerce el asiento contra su cuerpo. Compara esto con su peso usando una razón. (b) Calcula la dirección y la magnitud de la fuerza total que ejerce el asiento contra su cuerpo.

44. Repite el problema anterior para una situación en la que el cohete propulsor desacelera a una velocidad de 201 m/s². En este problema, las fuerzas son ejercidas por el asiento y el cinturón de seguridad.

45. Un cuerpo de masa de 2.00 kg es empujado hacia arriba por una fuerza vertical de 25.0 N. ¿Cuál es su aceleración?

46. ​​Un automóvil que pesa 12.500 N comienza desde el reposo y acelera a 83.0 km/h en 5.00 s. La fuerza de fricción es 1350 N. Encuentra la fuerza aplicada producida por el motor.

47. Se supone que un cuerpo con una masa de 10.0 kg está en el campo gravitatorio de la Tierra con g = 9.80 m/s². ¿Cuál es su aceleración?

48. Un bombero tiene masa m; escucha la alarma de incendios y se desliza por el poste con la aceleración a (que es menor que g en magnitud). (a) Escribe una ecuación que dé la fuerza vertical que debe aplicar al poste. (b) Si su masa es de 90.0 kg y acelera a 5.00 m/s², ¿cuál es la magnitud de su fuerza aplicada?

49. Un receptor de béisbol está realizando un truco para un comercial de televisión. Atrapará una pelota de béisbol (masa 145 g) caída desde una altura de 60.0 m sobre su guante. Su guante detiene la pelota en 0.0100 s. ¿Cuál es la fuerza ejercida por su guante sobre la pelota?

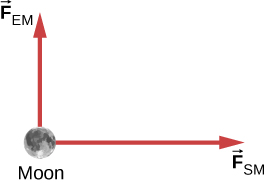
50. Cuando la Luna está directamente sobre tu cabeza al atardecer, la fuerza de la Tierra sobre la Luna, FEMFEM, está esencialmente a 90 ° 90 ° de la fuerza del Sol en la Luna, FSMFSM, como se muestra a continuación. Dado que F_EM = 1.98 × 10²⁰ N y F_FS = 4.36 × 10²⁰ N, ​​todas las demás fuerzas en la Luna son insignificantes, y la masa de la Luna es 7.35 × 10²² kg, determina la magnitud de la aceleración de la Luna

5.6 La tercera Ley de Newton

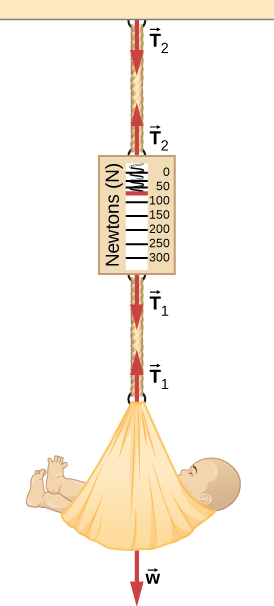
51. (a) ¿Qué fuerza externa neta se ejerce sobre un proyectil de artillería de 1100.0 kg disparado desde un acorazado si el caparazón se acelera a 2.40 × 10⁴ m/s²? (b) ¿Cuál es la magnitud de la fuerza ejercida sobre el buque por el proyectil de artillería y por qué?

52. Un jugador de rugby valiente pero insuficiente es empujado hacia atrás por un jugador contrario que ejerce una fuerza de 800.0 N sobre él. La masa del jugador perdedor mas su equipo es de 90.0 kg y está acelerando hacia atrás a 1.20 m². (a) ¿Cuál es la fuerza de fricción entre los pies del jugador que pierde y la hierba? (b) ¿Qué fuerza ejerce el jugador ganador en el suelo para avanzar si su masa más equipo es de 110.0 kg?

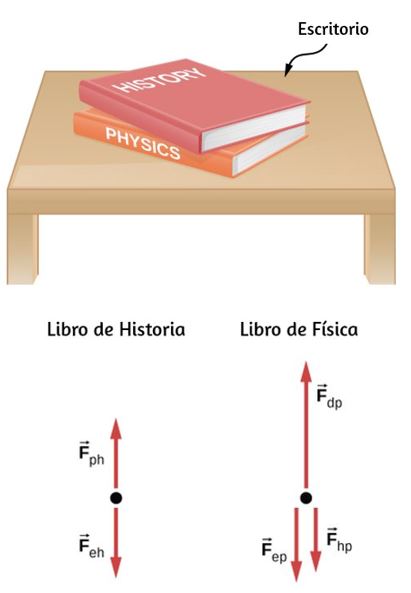
53. Un libro de historia está sobre un libro de física en un escritorio, como se muestra a continuación; un diagrama de cuerpo libre también se muestra. Los libros de historia y física pesan 14 N y 18 N, respectivamente. Identifica cada fuerza en cada libro con una notación de subíndice doble (por ejemplo, la fuerza de contacto del libro de historia presionando contra el libro de física se puede describir como F→_HP) y determina el valor de cada una de estas fuerzas, explicando el proceso utilizado



54. Un camión colisiona con un automóvil, y durante la colisión, la fuerza neta en cada vehículo es esencialmente la fuerza ejercida por el otro. Supongamos que la masa del automóvil es de 550 kg, la masa del camión es de 2200 kg y la magnitud de la aceleración del camión es de 10 m/s². Encuentra la magnitud de la aceleración del automóvil.

5.7 Fuerzas comunes

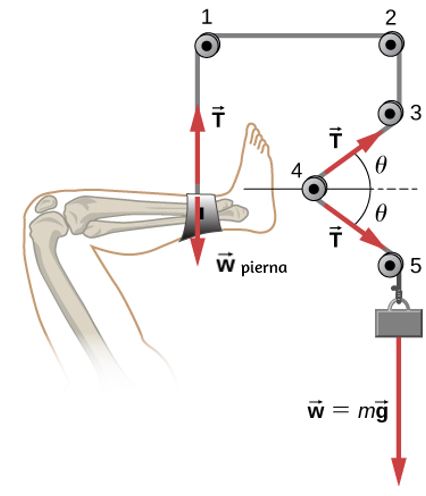
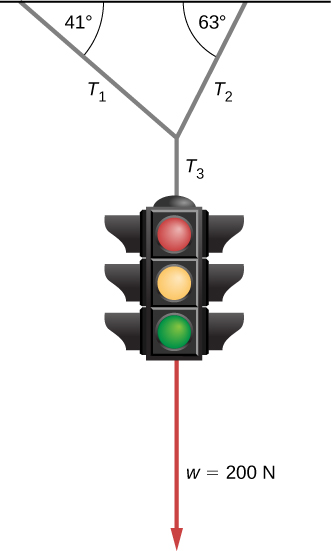
55. Una pierna está suspendida en un sistema de tracción, como se muestra a continuación. (a) ¿Qué polea en la figura se usa para calcular la fuerza ejercida sobre el pie? (b) ¿Cuál es la tensión en la cuerda? Aquí T→ es la tensión, w→_pierna es el peso de la pierna, y w→ es el peso de la carga que proporciona la tensión.



56. Suponga que la tibia en la imagen anterior era un fémur en una configuración de tracción para un hueso roto, con poleas y cuerda disponibles. ¿Cómo podríamos aumentar la fuerza a lo largo del fémur con el mismo peso?

57. Dos equipos de nueve miembros cada uno participan en el tira y afloja. Cada uno de los miembros del primer equipo tiene una masa promedio de 68 kg y ejerce una fuerza promedio de 1350 N horizontalmente. Cada uno de los miembros del segundo equipo tiene una masa promedio de 73 kg y ejerce una fuerza promedio de 1365 N horizontalmente. (a) ¿Cuál es la magnitud de la aceleración de los dos equipos y qué equipo gana? (b) ¿Cuál es la tensión en la sección de la cuerda entre los equipos?

58. ¿Qué fuerza tiene que aplicar un trampolín a Jennifer, una gimnasta de 45.0 kg, para acelerarla directamente a 7.50 m/s²? La respuesta es independiente de la velocidad de la gimnasta: puede moverse hacia arriba o hacia abajo o puede estar instantáneamente inmóvil.

59. (a) Calcula la tensión en una hebra vertical de telaraña si una araña de masa 2.00 × 10^-5 kg cuelga inmóvil sobre ella. (b) Calcula la tensión en una hebra horizontal de telaraña si la misma araña se encuentra inmóvil en el medio de ella, muy parecido al equilibrista de la figura 5.26. El hilo se hunde en un ángulo de 12° por debajo de la horizontal. Compara esto con la tensión en el cordón vertical (encuentra su relación).

60. Supón que Kevin, un gimnasta de 60.0 kg, sube una cuerda. (a) ¿Cuál es la tensión en la cuerda si sube a una velocidad constante? (b) ¿Cuál es la tensión en la cuerda si acelera hacia arriba a una velocidad de 1.50 m/s²?

61. Demuestra que, como se explica en el texto, una fuerza F⊥ ejercida sobre un medio flexible en su centro y perpendicular a su longitud (como en el cable de la cuerda floja de la figura 5.26) da lugar a una tensión de magnitud T = F⊥/2sin(θ).

62. Considera la figura 5.28. El conductor intenta sacar el auto del barro ejerciendo una fuerza perpendicular de 610.0 N, y la distancia que empuja en el medio de la cuerda es de 1.00 m mientras se encuentra a 6.00 m del automóvil de la izquierda y a 6.00 m de distancia del árbol a la derecha. ¿Cuál es la tensión T en la cuerda, y cómo se encuentra la respuesta?
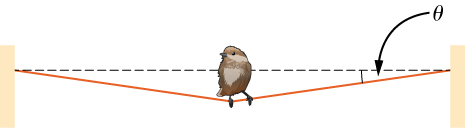
63. Un pájaro tiene una masa de 26 g y se encuentra en el medio de una línea telefónica extendida. (a) Demuestra que la tensión en la línea puede calcularse usando la ecuación T = mg/2senθ. Determina la tensión cuando (b) θ = 5° y (c) θ = 0.5°. Supongamos que cada mitad de la línea es recta.



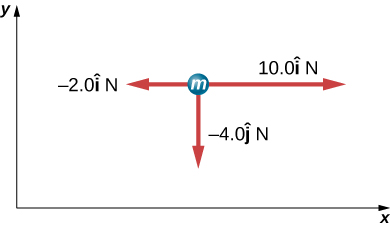
64. Un extremo de una cuerda de 30 m está atado a un árbol; el otro extremo está atado a un auto atrapado en el barro. El automovilista tira hacia un lado en el punto medio de la cuerda, desplazándola una distancia de 2 m. Si ejerce una fuerza de 80 N en estas condiciones, determina la fuerza ejercida sobre el automóvil.

65. Considera el peso del bebé en la siguiente figura. (a) ¿Cuál es la masa del bebé y la canasta si se observa una lectura a escala de 55 N? (b) ¿Cuánto es la tensión T₁ en el cordón que une al bebé a la báscula? (c) ¿Cuál es la tensión T₂ en el cable que une la báscula al techo, si la báscula tiene una masa de 0.500 kg? (d) Dibuja la situación, indicando el sistema de interés utilizado para resolver cada parte. Las masas de las cuerdas son insignificantes.



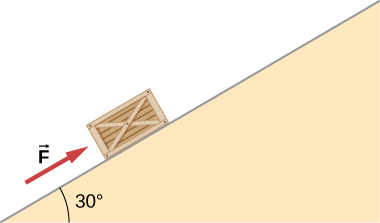
66. ¿Qué fuerza debe aplicarse a una caja de 100.0 kg en un plano sin fricción inclinado a 30° para provocar una aceleración de 2.0 m/s² en el plano?



67. Un bloque de 2,0 kg se encuentra en una rampa perfectamente lisa que forma un ángulo de 30° con la horizontal. (a) ¿Cuál es la aceleración del bloque por la rampa y la fuerza de la rampa en el bloque? (b) ¿Qué fuerza aplicada hacia arriba a lo largo y paralela a la rampa permitiría que el bloque se mueva con velocidad constante?

5.8 Dibujando diagramas de cuerpo libre

68. Una bola de masa m cuelga en reposo, suspendida por una cuerda. (a) Bosqueja todas las fuerzas. (b) Dibuja el diagrama de cuerpo libre para la bola.

69. Un automóvil se mueve a lo largo de un camino horizontal. Dibuja un diagrama de cuerpo libre; asegúrate de incluir la fricción de la carretera que se opone al movimiento hacia delante del automóvil.

70. Un corredor empuja contra la pista, como se muestra en las siguiente figura. (a) Proporciona un diagrama de cuerpo libre que muestre todas las fuerzas sobre el corredor. (Sugerencia: coloca todas las fuerzas en el centro de su cuerpo e incluyea su peso.) (B) Brinda un diagrama revisado que muestre los componenetes rectangulares en x e y.



71. UN semáforo cuelga de los cables como se muestra en la siguiente figura. Dibuja un diagrama de cuerpo libre en un plano de coordenadas para esta situación.

Problemas adicionales

72. Dos fuerzas pequeñas, F→₁ = -2.40i^ - 6.10tj^ N y F→₂ = 8.50i^ - 9.70j^ N, se ejercen en un asteroide rebelde por un par de tractores espaciales. (a) Encuentra la fuerza neta. (b) ¿Cuál es la magnitud y dirección de la fuerza neta? (c) Si la masa del asteroide es de 125 kg, ¿qué aceleración experimenta (en forma de vector)? (d) ¿Cuál es la magnitud y la dirección de la aceleración?

73. Dos fuerzas de 25 y 45 N actúan sobre un objeto. Sus direcciones difieren en 70°. La aceleración resultante tiene una magnitud de 10.0 m/s². ¿Cuál es la masa del cuerpo?

74. Una fuerza de 1600 N actúa paralela a una rampa para empujar un piano de 300 kg dentro de una furgoneta. La rampa está inclinada a 20°. (a) ¿Cuál es la aceleración del piano por la rampa? (b) ¿Cuál es la velocidad del piano cuando alcanza la parte superior si la rampa tiene 4.0 m de largo y el piano comienza desde el reposo?

75. Dibuja un diagrama de cuerpo libre de un buzo que ha entrado en el agua, se movió hacia abajo, y es influenciado por una fuerza hacia arriba debido al agua que equilibra el peso (es decir, el buzo está suspendido).

76. Para un nadador que acaba de saltar de un trampolín, supón que la resistencia del aire es insignificante. El nadador tiene una masa de 80.0 kg y salta de una tabla a 10.0 m por encima del agua. Tres segundos después de entrar en el agua, se detiene su movimiento hacia abajo. ¿Qué fuerza promedio hacia arriba ejerció el agua sobre él?

77. (a) Encuentra una ecuación para determinar la magnitud de la fuerza neta requerida para detener un automóvil de masa m, dado que la velocidad inicial del automóvil es v₀ y la distancia de frenado es x. (b) Encuentre la magnitud de la fuerza neta si la masa del automóvil es de 1050 kg, la velocidad inicial es de 40.0 km/h, y la distancia de frenado es de 25.0 m.

78. Un velero tiene una masa de 1.50 × 10³ kg y está afectado por una fuerza de 2.00 × 10³ N hacia el este, mientras que el viento actúa detrás de las velas con una fuerza de 3.00 × 10³ N en una dirección 45° al noreste. Encuentra la magnitud y dirección de la aceleración resultante.
79. Encuentra la aceleración del cuerpo de masa 10.0 kg que se muestra a continuación.



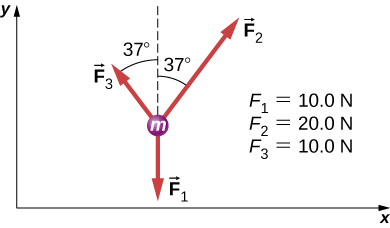
80. Un cuerpo de masa de 2,0 kg se mueve a lo largo del eje x con una velocidad de 3.0 m/s en el instante representado a continuación. (a) ¿Cuál es la aceleración del cuerpo? (b) ¿Cuál es la velocidad del cuerpo 10.0 segundos después? (c) ¿Cuál es su desplazamiento después de 10.0 s?



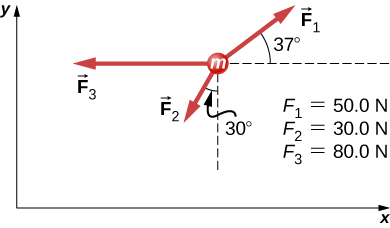
81. La fuerza F→_B tiene el doble de la magnitud de la fuerza F→_A. Encuentra la dirección en la que la partícula se acelera en esta figura.



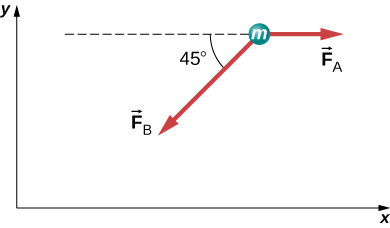
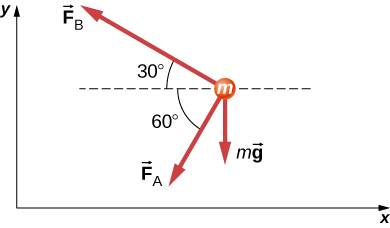
82. A continuación se muestra un cuerpo de 1.0 kg de masa bajo la influencia de las fuerzas F→_A, F→_B y mg→. Si el cuerpo acelera hacia la izquierda a 20 m/s², ¿qué son F→_A y F→_B?



83. Una fuerza actúa sobre un automóvil de masa m de modo que la velocidad v del automóvil aumenta con la posición x como v = kx², donde k es constante y todas las cantidades están en unidades SI. Encuentra la fuerza que actúa sobre el automóvil en función de la posición.

84. Una fuerza de 7.0 N paralela a una inclinación se aplica a una caja de 1.0 kg. La rampa está inclinada a 20° y no tiene fricción. (a) ¿Cuál es la aceleración de la caja? (b) Si todas las demás condiciones son las mismas pero la rampa tiene una fuerza de fricción de 1.9 N, ¿cuál es la aceleración?

85. Dos bloques, A y B, están en reposo. El bloque A está en un terreno llano, mientras que el bloque B descansa sobre un plano inclinado en un ángulo θ con la horizontal. (a) Escribe expresiones para la fuerza normal que actúa en cada bloque. (b) Compare las dos fuerzas; es decir, cuál es más grande o si son iguales en magnitud. (c) Si el ángulo de inclinación es 10°, ¿qué fuerza es mayor?

86. Una masa de 250.0 g está suspendida de un resorte que cuelga verticalmente. El resorte se estira 6.00 cm. ¿Cuánto se estirará el resorte si la masa suspendida es de 530.0 g?

87. Como se muestra a continuación, dos muelles idénticos, cada uno con la constante de resorte 20 N/m, soportan un peso de 15,0 N. (a) ¿Cuál es la tensión en el resorte A? (b) ¿Cuál es la cantidad de estiramiento del muelle A desde la posición de descanso?



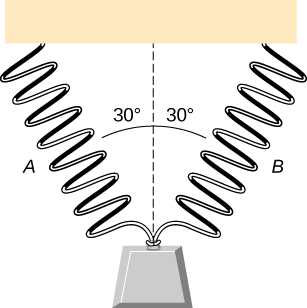
88. A continuación se muestra un bloque de 30,0 kg apoyado en una rampa sin fricción inclinada a 60° con respecto a la horizontal. El bloque está sostenido por un resorte que se estira 5.0 cm. ¿Cuál es la fuerza constante del resorte?



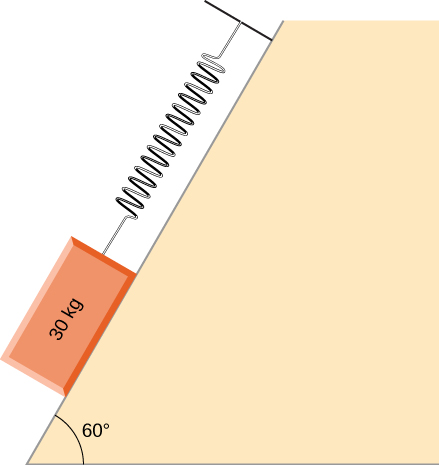
89. Al construir una casa, los carpinteros usan clavos de una caja grande. La caja se suspende de un resorte dos veces durante el día para medir el uso de los clavos. Al comienzo del día, el resorte se estira 50 cm. Al final del día, el resorte se extiende 30 cm. ¿Qué fracción o porcentaje de los clavos se han utilizado?

90. Se aplica una fuerza a un bloque para moverlo hacia arriba en una inclinación de 30°. La inclinación es sin fricción. Si F = 65.0 N y M = 5.00 kg, ¿cuál es la magnitud de la aceleración del bloque?



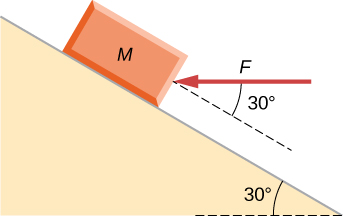
91. Se aplican dos fuerzas a un objeto de 5.0 kg y se acelera a una velocidad de 2.0 m/s² en la dirección y positiva. Si una de las fuerzas actúa en la dirección x positiva con magnitud 12.0 N, encuentra la magnitud de la otra fuerza.

92. El bloque de la derecha que se muestra a continuación tiene más masa que el bloque de la izquierda (m₂ > m₁). Dibuja diagramas de cuerpo libre para cada bloque.

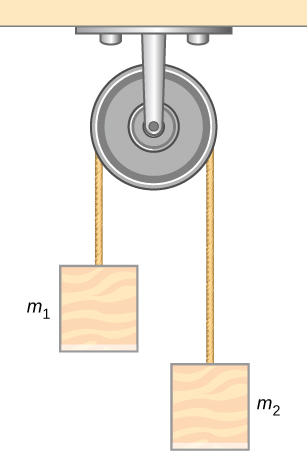
Problemas reto

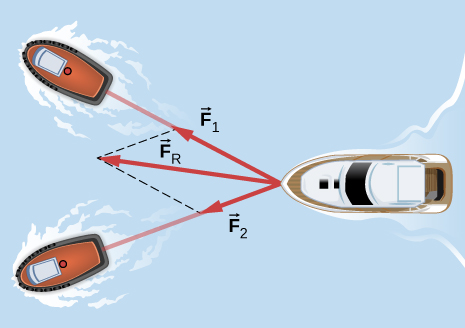
93. Si dos remolcadores tiran de un buque deshabilitado, como se muestra aquí en una vista aérea, la embarcación deshabilitada será arrastrada en la dirección indicada por el resultado de las fuerzas ejercidas. (a) Dibuja un diagrama de cuerpo libre para el buque. Supón que ninguna fricción o fuerza de arrastre afecta el buque. (b) ¿Incluye todas las fuerzas en la vista superior en tu diagrama de cuerpo libre? ¿Por qué o por qué no?



94. Un objeto de 10.0 kg se mueve inicialmente hacia el este a 15.0 m/s. Entonces una fuerza actúa sobre él durante 2.00 s, luego de lo cual se mueve al noroeste, también a 15.0 m/s. ¿Cuál es la magnitud y la dirección de la fuerza promedio que actuó sobre el objeto durante el intervalo de 2.00 s?

95. El 25 de junio de 1983, el lanzador de bala Udo Beyer de Alemania del Este lanzó el tiro de 7.26 kg a 22.22 m, que en ese momento era un récord mundial. (a) Si el disparo se liberó a una altura de 2.20 m con un ángulo de proyección de 45.0°, ¿cuál fue su velocidad inicial? (b) Si, mientras estaba en la mano de Beyer, el disparo se aceleró uniformemente en una distancia de 1,20 m, ¿cuál fue la fuerza neta sobre él?

96. Un cuerpo de masa m se mueve en una dirección horizontal tal que en el tiempo t su posición está dada por x (t) = at⁴ + bt³ + ct, donde a, b, y c son constantes. (a) ¿Cuál es la aceleración del cuerpo? (b) ¿Cuál es la fuerza dependiente del tiempo que actúa sobre el cuerpo?

97. Un cuerpo de masa m tiene una velocidad inicial v₀ en la dirección x positiva. Es actuado por una fuerza constante F en el tiempo t hasta que la velocidad se vuelve cero; la fuerza continúa actuando sobre el cuerpo hasta que su velocidad se convierte en -v₀ en la misma cantidad de tiempo. Escribe una expresión para la distancia total que recorre el cuerpo en términos de las variables indicadas.

98. Las velocidades de un objeto de 3.0 kg en t = 6.0 s y t = 8.0 s son (3.0i^ - 6.0j^ + 4.0k^) m/s y (-2.0i^ + 4.0k^) m/s, respectivamente. Si el objeto se mueve a una aceleración constante, ¿cuál es la fuerza que actúa sobre él?

99. Un astronauta de 120 kg viaja en un trineo cohete que se desliza a lo largo de un plano inclinado. El trineo tiene una componente horizontal de aceleración de 5.0 m/s² y un componente descendente de 3.8 m/s². Calcula la magnitud de la fuerza sobre el jinete por el trineo. (Sugerencia: recuerda que se debe considerar la aceleración gravitacional).

100. Dos fuerzas actúan sobre un objeto de 5.0 kg que se mueve con una aceleración de 2.0 m/s² en la dirección y positiva. Si una de las fuerzas actúa en la dirección x positiva y tiene una magnitud de 12 N, ¿cuál es la magnitud de la otra fuerza?

101. Supongamos que estás viendo un juego de fútbol desde un helicóptero sobre el campo de juego. Dos jugadores de fútbol patean simultáneamente una pelota de fútbol estacionaria en el campo llano; el balón de fútbol tiene una masa de 0.420 kg. El primer jugador patea con fuerza 162 N a 9.0° al noroeste. En el mismo instante, el segundo jugador patea con fuerza 215 N a 15° al sureste. Encuentra la aceleración de la bola en la forma i^ y j^.

102. Una masa de 10.0 kg cuelga de un resorte que tiene una constante de resorte de 535 N/m. Encuentra la posición final del resorte lejos de su posición de descanso. (Usa g = 9.80 m/s².)

103. Un par de dados difusos de 0.0502 kg se une al espejo retrovisor de un automóvil con una cuerda corta. El automóvil acelera a velocidad constante, y los dados cuelgan en un ángulo de 3.20° desde la vertical debido a la aceleración del automóvil. ¿Cuál es la magnitud de la aceleración del automóvil?

104. En un circo, un burro tira de un trineo que lleva un pequeño payaso con una fuerza dada por 2.48i^ + 4.33j^ N. Un caballo tira del mismo trineo, ayudando al desventurado burro, con una fuerza de 6.56i^ + 5.33j^ N. La masa del trineo es de 575 kg. Usando la forma i^ y j^ para la respuesta a cada problema, encuentra (a) la fuerza neta en el trineo cuando los dos animales actúen juntos, (b) la aceleración del trineo, y (c) la velocidad después de 6.50 s.

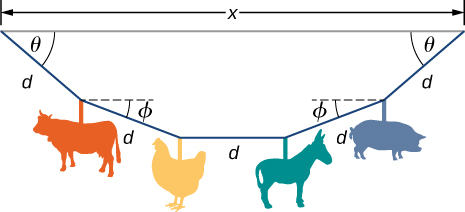
105. Colgando del techo sobre una cama de bebé, fuera del alcance del bebé, hay una cuerda con formas de plástico, como se muestra aquí. La cuerda está tensa (no hay holgura), como se muestra en los segmentos rectos. Cada forma de plástico tiene la misma masa m, y están igualmente espaciados por una distancia d, como se muestra. Los ángulos etiquetados como θ describen el ángulo formado por el final de la cuerda y el techo en cada extremo. La longitud del centro es horizontal. Los dos segmentos restantes forman un ángulo con la horizontal, etiquetados como φ. Deje que T₁ sea la tensión en la sección más a la izquierda de la cuerda, T₂ sea la tensión en la sección adyacente a ella, y T₃ sea la tensión en el segmento horizontal. (a) Encuentra una ecuación para la tensión en cada sección de la cuerda en términos de las variables m, g, y θ. (b) Encuentra el ángulo φ en términos del ángulo θ. (c) Si θ = 5.10°, ¿cuál es el valor de φ? (d) Encuentra la distancia x entre los puntos finales en términos de d y θ.



106. Un disparo de bala de un rifle tiene una masa de 10.0 g y viaja hacia la derecha a 350 m/s. Golpea un objetivo, una gran bolsa de arena, penetrándolo a una distancia de 34.0 cm. Encuentra la magnitud y la dirección de la fuerza de retardo que ralentiza y detiene la bala.

107. Un objeto es actuado por tres fuerzas simultáneas: F→₁ = (- 3.00i^ + 2.00j^) N, F→₂ = (6.00i^ - 4.00j^) N, y F⃗ 3 = (2.00i + 5.00j) F→₃ = (2.00i^ + 5.00j^) N. El objeto experimenta una aceleración de 4.23 m/s². (a) Encuentra el vector de aceleración en términos de m. (b) Encuentra la masa del objeto. (c) Si el objeto comienza desde el reposo, encuentre su velocidad después de los 5.00 s. (d) Encuentra los componentes de la velocidad del objeto después de 5.00 s.

108. En un acelerador de partículas, un protón tiene una masa de 1.67 × 10^-27 kg y una velocidad inicial de 2.00 × 10⁵ m/s. Se mueve en línea recta y su velocidad aumenta a 9.00 × 10⁵ m/s en una distancia de 10.0 cm. Supongamos que la aceleración es constante. Encuentra la magnitud de la fuerza ejercida sobre el protón.

109. Un dron está siendo dirigido a través de un lago cubierto de hielo sin fricción. La masa del dron es 1.50 kg, y su velocidad es 3.00i^ m/s. Después de 10.0 s, la velocidad es 9.00i^ + 4.00j^ m/s. Si una fuerza constante en la dirección horizontal está causando este cambio de movimiento, encuentra (a) las componentes de la fuerza y ​​(b) la magnitud de la fuerza.