Preguntas y problemas - Capítulo IV

Preguntas conceptuales

4.2 Vectores de desplazamiento y velocidad

1. ¿Qué forma tiene la trayectoria de una partícula si la distancia desde cualquier punto A al punto B es igual a la magnitud del desplazamiento de A a B?

2. Da un ejemplo de una trayectoria en dos o tres dimensiones causada por movimientos perpendiculares independientes.

3. Si la velocidad instantánea es cero, ¿qué se puede decir sobre la pendiente de la función de posición?

4.3 Vector de aceleración

4. Si la función de posición de una partícula es una función lineal del tiempo, ¿qué se puede decir acerca de su aceleración?

5. Si un objeto tiene una componente x constante de la velocidad y de repente experimenta una aceleración en la dirección y, ¿cambia la componente x de su velocidad?

6. Si un objeto tiene una componente x constante de velocidad y de repente experimenta una aceleración en un ángulo de 70° en la dirección x, ¿cambia la componente x de la velocidad?

4.4 Movimiento parabólico

7. Responde las siguientes preguntas para el movimiento parabólico en terreno llano suponiendo una resistencia al aire insignificante, con un ángulo inicial diferente de 0° y 90°: (a) ¿La velocidad es siempre cero? (b) ¿Cuándo es la velocidad un mínimo? ¿Un máximo? (c) ¿Puede la velocidad ser alguna vez la misma que la velocidad inicial en un momento distinto de at = 0? (d) ¿Puede la velocidad ser siempre la misma que la velocidad inicial en un momento distinto de t = 0?

8. Contesta las siguientes preguntas para el movimiento parábolico en terreno llano suponiendo una resistencia al aire insignificante, con el ángulo inicial diferente de 0° y 90°: (a) ¿La aceleración es nula? (b) ¿La aceleración está siempre en la misma dirección que una componente de la velocidad? (c) ¿La aceleración es siempre opuesta en dirección a una componente de velocidad?

9. Una moneda de 500 pesos se coloca en el borde de una mesa para que cuelgue un poco. Una moneda de 100 pesos se desliza horizontalmente en la superficie de la mesa perpendicular al borde y golpea la cabeza de la moneda de $500. ¿Qué moneda golpea el suelo primero?

4.5 Movimiento Circular Uniforme

10. ¿Puede la aceleración centrípeta cambiar la velocidad de una partícula en movimiento circular?

11. ¿Puede la aceleración tangencial cambiar la velocidad de una partícula en movimiento circular?

4.6 Movimiento relativo en una y dos dimensiones

12. ¿Qué marco o marcos de referencia usas instintivamente cuando conduces un automóvil? Al volar en un avión comercial?

13. Un jugador de baloncesto que corre por la cancha generalmente mantiene su mirada fija en los jugadores que lo rodean. Él se está moviendo rápido. ¿Por qué no necesita mantener sus ojos en la pelota?

14. Si alguien está montado en la parte trasera de una camioneta y lanza una pelota de softball directamente hacia atrás, ¿es posible que la pelota caiga directamente hacia abajo según la ve una persona parada al costado de la carretera? ¿Bajo qué condición ocurriría esto? ¿Cómo vería el movimiento de la bola la persona que lo arrojó?

15. El sombrero de un corredor que corre a velocidad constante cae de la parte posterior de su cabeza. Dibuja un boceto que muestre la ruta del sombrero en el marco de referencia del corredor. Dibuja su camino tal como lo ve un observador estacionario. Desprecia la resistencia del aire.

16. Un terrón de tierra cae de la cama de un camión en movimiento. Golpea el suelo directamente debajo del final del camión. (a) ¿Cuál es la dirección de su velocidad con respecto al camión justo antes de que golpee? (b) ¿Es esto lo mismo que la dirección de su velocidad relativa al suelo justo antes de que golpee? Explica tus respuestas

Problemas

4.2 Vectores de desplazamiento y velocidad

17. Las coordenadas de una partícula en un sistema de coordenadas rectangular son (1.0, -4.0, 6.0). ¿Cuál es el vector de posición de la partícula?

18. La posición de una partícula cambia de r→₁ = (2.0 i + 3.0j) cmr → 1 = (2.0i^ + 3.0j^)cm a r→₂ = (- 4.0i^ + 3.0j^) cm. ¿Cuál es el desplazamiento de la partícula?

19. El hoyo 18 en Pebble Beach Golf Course es un dogleg a la izquierda de longitud 496.0 m. La calle desde el tee se toma como la dirección x. Un golfista golpea su salida una distancia de 300.0 m, correspondiente a un desplazamiento Δr→₁ = 300.0 mi^, y su segundo golpe es de 189.0 m con un desplazamiento Δr→₂ = 172.0 mi^ + 80.3 mj^. ¿Cuál es el desplazamiento final de la pelota de golf desde el tee?

20. Un pájaro vuela recto al noreste una distancia de 95.0 km por 3.0 h. Con el eje x hacia el este y el eje y hacia el norte, ¿cuál es el desplazamiento en la notación vectorial unitaria para el ave? ¿Cuál es la velocidad promedio del viaje?

21. Un ciclista recorre 5.0 km hacia el este, luego 10.0 km 20° al noroeste. Desde este punto, corre 8.0 km hacia el oeste. ¿Cuál es el desplazamiento final desde donde comenzó el ciclista?

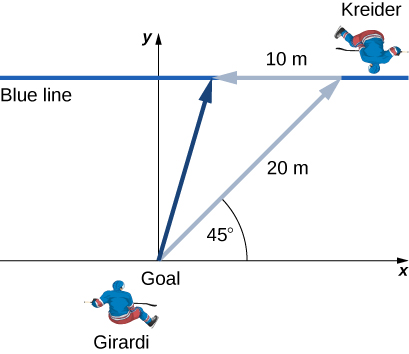
22. El defensa de los Vigilantes de Nueva York, Daniel Girardi, se para en la portería y pasa un disco de hockey 20 m y 45° desde la portería al ala izquierda Chris Kreider, quien espera en la línea azul. Kreider espera que Girardi llegue a la línea azul y pasa el disco directamente sobre el hielo a 10 m. ¿Cuál es el desplazamiento final del disco? Ver la siguiente figura.



23. La posición de una partícula es r→(t) = 4.0t²i^ - 3.0j^ + 2.0t³j^ km. (a) ¿Cuál es la velocidad de la partícula en 0 s y en 1.0 s? (b) ¿Cuál es la velocidad promedio entre 0 s y 1.0 s?

24. Clay Matthews, un defensor de los Green Bay Packers, puede alcanzar una velocidad de 10.0 m/s. Al comienzo de una jugada, Matthews corre hacia el jardín 45° con respecto a la yarda 50 y cubre 8.0 m en 1 s. Luego corre recto por el campo a 90° con respecto a la línea de 50 yardas por 12 m, con un tiempo transcurrido de 1.2 s. (a) ¿Cuál es el desplazamiento final de Matthews desde el comienzo de la jugada? (b) ¿Cuál es su velocidad promedio?

25. El F-35B Lighting II es un caza a reacción de despegue corto y aterrizaje vertical. Si realiza un despegue vertical a 20.00 m de altura sobre el suelo y luego sigue una trayectoria de vuelo en ángulo de 30° con respecto al suelo durante 20.00 km, ¿cuál es el desplazamiento final?

4.3 Vector de aceleración

26. La posición de una partícula es r→(t) = (3.0t²i^ + 5.0j^ - 6.0tk^) m. (a) Determina su velocidad y aceleración como funciones del tiempo. (b) ¿Cuál es su velocidad y aceleración en el tiempo t = 0?

27. La aceleración de una partícula es (4.0i^ + 3.0j^) m / s2. (4.0i ^ + 3.0j ^) m/s². En t = 0, su posición y velocidad son cero. (a) ¿Cuál es la posición y la velocidad de la partícula como funciones del tiempo? (b) Encuentre la ecuación de la trayectoria de la partícula. Dibuja los ejes x e y, y dibuja la trayectoria de la partícula.

28. Un barco sale del muelle en t = 0 y se dirige a un lago con una aceleración de 2.0 m/s²i^. Un fuerte viento empuja el barco, dándole una velocidad adicional de 2.0 m/si^ + 1.0 m/sj^. (a) ¿Cuál es la velocidad del barco en t = 10 s? (b) ¿Cuál es la posición del barco en t = 10 s? Dibuja un boceto de la trayectoria y posición de la embarcación en t = 10 s, mostrando los ejes x e y.

29. La posición de una partícula para t> 0 viene dada por r→(t) = (3.0t²i^ - 7.0t³j^ - 5.0t^-2k^) m. (a) ¿Cuál es la velocidad en función del tiempo? (b) ¿Cuál es la aceleración en función del tiempo? (c) ¿Cuál es la velocidad de la partícula en t = 2.0 s? (d) ¿Cuál es su velocidad en t = 1.0 s y t = 3.0 s? (e) ¿Cuál es la velocidad promedio entre t = 1.0 s y t = 2.0 s?

30. La aceleración de una partícula es una constante. En t = 0 la velocidad de la partícula es (10i^ + 20j^) m/s. En t = 4 s la velocidad es 10j^ m/s. (a) ¿Cuál es la aceleración de la partícula? (b) ¿Cómo varían la posición y la velocidad con el tiempo? Supongamos que la partícula está inicialmente en el origen.

31. Una partícula tiene una función de posición r→(t) = cos (1.0t)i^ + sen(1.0t)j^ + tk^, donde los argumentos de las funciones seno y seno están en radianes. (a) ¿Cuál es el vector de velocidad? (b) ¿Cuál es el vector de aceleración?

32. Un avión Lockheed Martin F-35 II Lighting despega de un portaaviones con una longitud de pista de 90 m y una velocidad de despegue de 70 m/s al final de la pista. Los jets son catapultados al espacio aéreo desde la cubierta de un portaaviones con dos fuentes de propulsión: la propulsión a chorro y la catapulta. En el punto de salir de la cubierta del portaaviones, la aceleración del F-35 disminuye a una aceleración constante de 5.0 m/s² a 30° con respecto a la horizontal. (a) ¿Cuál es la aceleración inicial del F-35 en la cubierta del portaaviones para que sea aerotransportado? (b) Escribe la posición y la velocidad del F-35 en la notación vectorial unitaria desde el punto en que sale de la cubierta del portaaviones. (c) ¿A qué altura está el caza 5.0 s después de que abandona la cubierta del portaaviones? (d) ¿Cuál es su velocidad y rapidez en este momento? (e) ¿Qué tan lejos ha viajado horizontalmente?

4.4 Movimiento parabólico

33. Una bala se dispara horizontalmente desde la altura del hombro (1.5 m) con una velocidad inicial de 200 m/s. (a) ¿Cuánto tiempo transcurre antes de que la bala toque el suelo? (b) ¿Qué distancia recorre la bala horizontalmente?

34. Una canica rueda sobre una mesa de 1.0 m de alto y golpea el piso en un punto a 3.0 m del borde de la mesa en dirección horizontal. (a) ¿Cuánto dura la canica en el aire? (b) ¿Cuál es la velocidad de la canica cuando sale del borde de la mesa? (c) ¿Cuál es su velocidad cuando golpea el piso?

35. Un dardo se lanza horizontalmente a una velocidad de 10 m/s en el blanco de un tablero de dardos a 2,4 m de distancia, como en la siguiente figura. (a) ¿Qué tan lejos está el dardo por debajo del objetivo deseado? (b) ¿Qué te dice tu respuesta sobre qué tan hábiles los jugadores de dardos lanzan sus dardos?

36. Un avión que vuela horizontalmente con una velocidad de 500 km/h a una altura de 800 m deja caer una caja de suministros (véase la figura siguiente). Si el paracaídas no se abre, ¿qué tan lejos del punto de lanzamiento cae la caja al suelo?



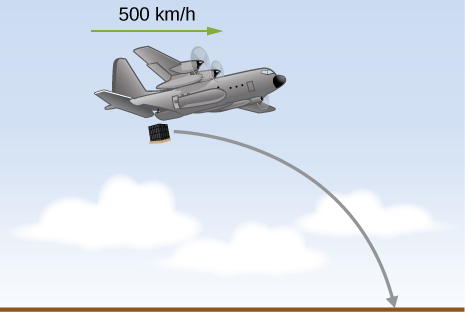
37. Suponga que el avión en el problema anterior dispara un proyectil horizontalmente en su dirección de movimiento a una velocidad de 300 m/s con respecto al plano. (a) ¿Cuán lejos toca el proyectil al frente del punto de lanzamiento? (b) ¿Cuál es su velocidad cuando toca el suelo?

38. Un lanzador de bola rápida puede lanzar una pelota de béisbol a una velocidad de 40 m/s (90 mi/h). (a) Suponiendo que el lanzador puede soltar la pelota a 16.7 m del plato de home para que la pelota se mueva horizontalmente, ¿cuánto tiempo tarda la pelota en llegar al plato de home? (b) ¿Qué distancia cae la pelota entre la mano del lanzador y el plato de home?

39. Se lanza un proyectil en un ángulo de 30° y aterriza 20 s más tarde a la misma altura que se lanzó. (a) ¿Cuál es la velocidad inicial del proyectil? (b) ¿Cuál es la altitud máxima? (c) ¿Cuál es el rango? (d) Calcule el desplazamiento desde el punto de lanzamiento hasta la posición en su trayectoria a los 15 s.

40. Un jugador de baloncesto dispara hacia una canasta a 6.1 m de distancia y 3.0 m sobre el piso. Si la bola se libera a 1.8 m sobre el piso en un ángulo de 60° sobre la horizontal, ¿cuál debe ser la velocidad inicial si pasa a través de la canasta?

41. En un instante particular, un globo de aire caliente está a 100 m en el aire y desciende a una velocidad constante de 2.0 m/s. En este instante exacto, una niña lanza una pelota horizontalmente, en relación con ella, con una velocidad inicial de 20 m/s. Cuando ella aterrice, ¿dónde encontrará la pelota? Ignora la resistencia del aire.

42. Un hombre en una motocicleta que viaja a una velocidad uniforme de 10 m/s arroja una lata vacía directamente hacia arriba con una velocidad inicial de 3.0 m/s. Encuentra la ecuación de la trayectoria vista por un oficial de policía al costado de la carretera. Supón que la posición inicial de la lata es el punto donde se lanza. Ignora la resistencia del aire.

43. Un atleta puede saltar una distancia de 8.0 m en el salto ancho. ¿Cuál es la distancia máxima que el atleta puede saltar en la Luna, donde la aceleración gravitacional es una sexta parte de la de la Tierra?

44. La distancia horizontal máxima que un niño puede lanzar una pelota es de 50 m. Supongamos que puede lanzar con la misma velocidad inicial en todos los ángulos. ¿Qué tan alto arroja la pelota cuando la lanza hacia arriba?

45. Una roca es arrojada desde un acantilado en un ángulo de 53° con respecto a la horizontal. El acantilado tiene 100 m de altura. La velocidad inicial de la roca es 30 m/s. (a) ¿Qué tan alto sobre el borde del acantilado se levanta la roca? (b) ¿Cuánto se ha movido horizontalmente cuando está a la altitud máxima? (c) ¿Cuánto tiempo después del lanzamiento toca el piso? (d) ¿Cuál es el rango de la roca? (e) ¿Cuáles son las posiciones horizontales y verticales de la roca en relación con el borde del acantilado en t = 2.0 s, t = 4.0 s, y t = 6.0 s?

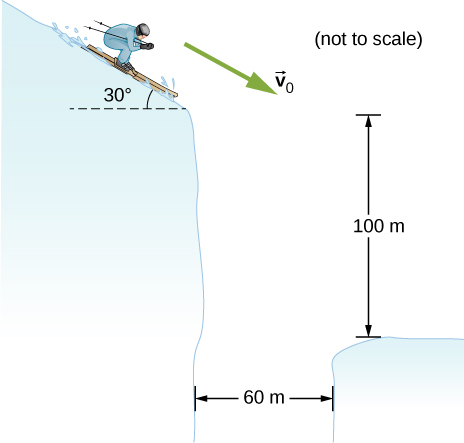
46. ​​Tratando de escapar de sus perseguidores, un agente secreto esquiva una pendiente inclinada 30° por debajo de la horizontal a 60 km/h. Para sobrevivir y aterrizar en la nieve a 100 m por debajo, debe despejar un desfiladero de 60 m de ancho. ¿Lo hace? Ignora la resistencia del aire.



47. Un golfista en una calle está a 70 m del green, que se encuentra debajo del nivel de la calle por 20 m. Si el golfista golpea la pelota en un ángulo de 40° con una velocidad inicial de 20 m/s, ¿qué tan cerca del green viene?

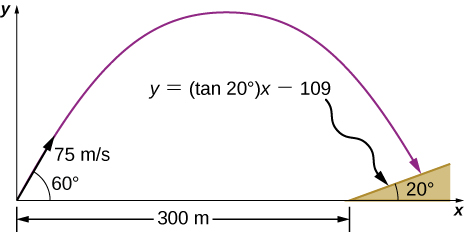
48. Un proyectil se dispara en una colina, cuya base está a 300 m de distancia. El proyectil se dispara a 60° por encima de la horizontal con una velocidad inicial de 75 m/s. La colina se puede aproximar por un plano inclinado a 20° con respecto a la horizontal. En relación con el sistema de coordenadas que se muestra en la siguiente figura, la ecuación de esta línea recta es y = (tan20°)x - 109. ¿Dónde en la colina aterriza el proyectil?



49. Un astronauta en Marte patea una pelota de fútbol en un ángulo de 45° con una velocidad inicial de 15 m/s. Si la aceleración de la gravedad en Marte es de 3.7 m/s², (a) ¿cuál es el alcance de la patada de fútbol en una superficie plana? (b) ¿Cuál sería el rango de la misma patada en la Luna, donde la gravedad es una sexta parte de la de la Tierra?

50. Mike Powell tiene el récord para el salto de longitud de 8.95 m, establecido en 1991. Si dejó el suelo en un ángulo de 15°, ¿cuál fue su velocidad inicial?

51. El robot guepardo del MIT puede saltar obstáculos de 46 cm de alto y tiene una velocidad de 12.0 km/h. (a) Si el robot se lanza a un ángulo de 60° a esta velocidad, ¿cuál es su altura máxima? (b) ¿Cuál debería ser el ángulo de lanzamiento para alcanzar una altura de 46 cm?

52. Mt. Asama, Japón, es un volcán activo. En 2009, una erupción arrojó rocas volcánicas sólidas que aterrizaron 1 km horizontalmente desde el cráter. Si las rocas volcánicas se lanzaron en un ángulo de 40° con respecto a la horizontal y aterrizaron a 900 m por debajo del cráter, (a) ¿cuál sería su velocidad inicial y (b) cuál es su tiempo de vuelo?

53. Drew Brees de los New Orleans Saints puede lanzar una pelota de fútbol de 23.0 m/s (50 mph). Si inclina el tiro a 10° de la horizontal, ¿a qué distancia llegará si se va a atrapar en la misma elevación que se arrojó?

54. El Vehículo Lunar Roving usado en las últimas misiones Apolo de la NASA alcanzó una rapidez no oficial de la superficie lunar de 5.0 m/s por el astronauta Eugene Cernan. Si el rover se estaba moviendo a esta velocidad sobre una superficie lunar plana y golpeaba una pequeña protuberancia que lo proyectaba fuera de la superficie en un ángulo de 20°, ¿cuánto tiempo estaría "en el aire" en la Luna?

55. Un arco de fútbol tiene 2,44 m de altura. Un jugador patea la pelota a una distancia de 10 m de la portería en un ángulo de 25°. ¿Cuál es la velocidad inicial del balón de fútbol?

56. Olympus Mons en Marte es el volcán más grande del sistema solar, a una altura de 25 km y con un radio de 312 km. Si estás parado en la cumbre, ¿con qué velocidad inicial deberías disparar un proyectil desde un cañón horizontalmente para despejar el volcán y aterrizar en la superficie de Marte? Ten en cuenta que Marte tiene una aceleración de la gravedad de 3.7 m/s².

57. En 1999, Robbie Knievel fue el primero en saltar el Gran Cañón en una motocicleta. En una parte estrecha del cañón (69.0 m de ancho) y viajando a 35.8 m/s fuera de la rampa de despegue, llegó al otro lado. ¿Cuál fue su ángulo de lanzamiento?

58. Lanzas una pelota de béisbol a una velocidad inicial de 15,0 m/s en un ángulo de 30° con respecto a la horizontal. ¿Cuál debería ser la velocidad inicial de la pelota a 30° en un planeta que tiene el doble de aceleración de la gravedad que la Tierra para alcanzar el mismo rango? Considera el lanzamiento y el impacto en una superficie horizontal.

59. Aaron Rogers lanza una pelota de fútbol a 20.0 m/s a ​​su receptor, que corre recto por el campo a 9.4 m/s durante 20.0 m. Si Aaron lanza el balón cuando el receptor ha llegado a 10.0 m, ¿qué ángulo tiene Aaron para lanzar la pelota para que el receptor la atrape en la marca de 20.0 m?

4.5 Movimiento Circular Uniforme

60. Un volante está girando a 30 rev/s. ¿Cuál es el ángulo total, en radianes, a través del cual un punto en el volante gira en 40 s?

61. Una partícula viaja en un círculo de radio de 10 m a una velocidad constante de 20 m/s. ¿Cuál es la magnitud de la aceleración?

62. Cam Newton de las Panteras de Carolina lanza una espiral de fútbol perfecta a 8.0 rev/s. El radio de un balón de fútbol profesional es de 8.5 cm en el medio del lado corto. ¿Cuál es la aceleración centrípeta de los laces en el fútbol?

63. Un paseo en el parque de atracciones hace girar a sus ocupantes dentro de un contenedor con forma de platillo volante. Si el recorrido circular horizontal que siguen los jinetes tiene un radio de 8.00 m, ¿a cuántas revoluciones por minuto están sujetos los jinetes sometidos a una aceleración centrípeta igual a la de la gravedad?

64. Un corredor que participa en la carrera de 200 m debe correr alrededor del final de una pista que tiene un arco circular con un radio de curvatura de 30.0 m. El corredor comienza la carrera a una velocidad constante. Si completa la carrera de 200 m en 23.2 s y corre a velocidad constante durante toda la carrera, ¿cuál es su aceleración centrípeta cuando corre la parte curva de la pista?

65. ¿Cuál es la aceleración de Venus hacia el Sol, asumiendo una órbita circular?

66. Un cohete jet experimental viaja alrededor de la Tierra a lo largo de su ecuador justo por encima de su superficie. ¿A qué velocidad debe viajar el avión si la magnitud de su aceleración es g?

67. Un ventilador está girando a una velocidad constante de 360.0 rev/min. ¿Cuál es la magnitud de la aceleración de un punto en una de sus hojas a 10.0 cm del eje de rotación?

68. Un punto ubicado en la segunda manecilla de un reloj grande tiene una aceleración radial de 0.1 cm/s². ¿Qué tan lejos está el punto del eje de rotación de la segunda mano?

4.6 Movimiento relativo en una y dos dimensiones

69. Los ejes de coordenadas del marco de referencia S' permanecen paralelos a los de S, ya que S' se aleja de S a una velocidad constante v→_SS' = (4.0i^ + 3.0j^ + 5.0k^ ) m/s. (a) Si en el momento t = 0 los orígenes coinciden, ¿cuál es la posición del origen O' en el marco S en función del tiempo? (b) ¿Cómo se relaciona la posición de la partícula para r→(t) y r→'(t), medida en S y S', respectivamente? (c) ¿Cuál es la relación entre las velocidades de partículas v→(t) y v→'(t)? (d) ¿Cómo se relacionan las aceleraciones a→(t) y a→'(t))?

70. Los ejes de coordenadas del cuadro de referencia S'S 'permanecen paralelos a los de S, ya que S' se aleja de S a una velocidad constante v→_S'S = (1.0i^ + 2.0k^ + 3.0k^t m/s. (a) Si en el momento t = 0 los orígenes coinciden, ¿cuál es la posición de origen O' en el marco S en función del tiempo? (b) ¿Cómo se relaciona la posición de la partícula para r→(t) y r→'(t), medida en S y S ', respectivamente? (c) ¿Cuál es la relación entre las velocidades de partículas v→(t) y v→'(t)? (d) ¿Cómo se relacionan las aceleraciones a→(t) y a→'(t)?

71. La velocidad de una partícula en el marco de referencia A es (2.0i^ + 3.0j^) m/s. La velocidad del marco de referencia A con respecto al marco de referencia B es de 4.0 k^)m/s, y la velocidad del marco de referencia B con respecto a C es de 2.0j^ m/s. ¿Cuál es la velocidad de la partícula en el marco de referencia C?

72. Las gotas de lluvia caen verticalmente a 4,5 m/s en relación con la tierra. ¿Qué mide un observador en un automóvil que se mueve a 22.0 m/s en línea recta como la velocidad de las gotas de lluvia?

73. Una gaviota puede volar a una velocidad de 9.00 m/s en aire quieto. (a) Si el pájaro tarda 20.0 min en viajar 6.00 km directamente hacia un viento que se aproxima, ¿cuál es la velocidad del viento? (b) Si el ave se da la vuelta y vuela con el viento, ¿cuánto tardará el pájaro en regresar 6.00 km?

74. Un barco zarpa desde Rotterdam, en dirección norte con 7,00 m/s en relación con el agua. La corriente oceánica local es de 1.50 m s en una dirección de 40.0° noreste. ¿Cuál es la velocidad del barco en relación con la Tierra?

75. Un bote puede ser remado a 8.0 km/h en aguas tranquilas. (a) ¿Cuánto tiempo se requiere para remar 1,5 km río abajo en un río que se mueve a 3.0 km/h en relación con la costa? (b) ¿Cuánto tiempo se requiere para el viaje de regreso? (c) ¿En qué dirección debe apuntar el bote para remar recto sobre el río? (d) Supongamos que el río tiene 0.8 km de ancho. ¿Cuál es la velocidad del barco con respecto a la Tierra y cuánto tiempo se requiere para llegar a la orilla opuesta? (e) Supongamos, en cambio, que el barco está apuntando directamente al otro lado del río. ¿Cuánto tiempo se requiere para cruzar y qué tan río abajo está el barco cuando llega a la orilla opuesta?

76. Un avión pequeño vuela a 200 km/h en aire quieto. Si el viento sopla directamente del oeste a 50 km/h, (a) en qué dirección debe el piloto dirigirse hacia el norte para cruzar directamente la tierra y (b) cuánto tiempo le lleva alcanzar un punto de 300 km directamente al norte de su punto de partida?

77. Un ciclista que viaja hacia el sudeste a lo largo de una carretera a 15 km/h siente un viento que sopla del sudoeste a 25 km/h. Para un observador estacionario, ¿cuál es la velocidad y la dirección del viento?

78. Un río se mueve hacia el este a 4 m/s. Un barco parte del muelle con rumbo 30° al noroeste a 7 m/s. Si el río tiene 1800 m de ancho, (a) ¿cuál es la velocidad del barco con respecto a la Tierra y (b) cuánto tiempo tarda el barco en cruzar el río?

Problemas adicionales

79. Un auto de carrera de Fórmula Uno viaja a 89.0 m/s a ​​lo largo de una pista recta, entra en un giro en la pista con un radio de curvatura de 200.0 m. ¿Qué aceleración centrípeta debe tener el automóvil para mantenerse en la pista?

80. Una partícula viaja en una órbita circular de radio de 10 m. Su velocidad está cambiando a una velocidad de 15.0 m/s² en un instante cuando su velocidad es de 40.0 m/s. ¿Cuál es la magnitud de la aceleración de la partícula?

81. El conductor de un automóvil que se mueve a 90.0 km/h presiona el freno cuando el automóvil entra en una curva circular de radio de 150.0 m. Si la velocidad del automóvil disminuye a una velocidad de 9.0 km/h cada segundo, ¿cuál es la magnitud de la aceleración del automóvil en el instante en que su velocidad es de 60.0 km/h?

82. Un auto de carrera que ingresa a la parte curva de la pista en Daytona 500 baja su velocidad de 85.0 m/s a ​​80.0 m/s en 2.0 s. Si el radio de la parte curva de la pista es 316.0 m, calcula la aceleración total del carro de carreras al comienzo y al final de la reducción de velocidad.

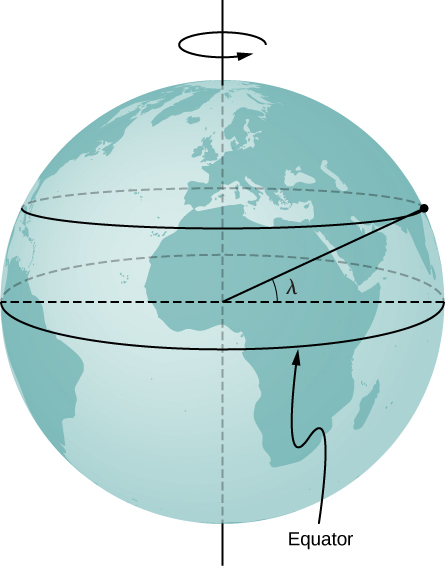
83. Un elefante se encuentra en la superficie de la Tierra a una latitud λ. Calcula la aceleración centrípeta del elefante como resultado de la rotación de la Tierra alrededor de su eje polar. Expresa tu respuesta en términos de λ, el radio R_E de la Tierra, y el tiempo T para una rotación de la Tierra. Compara tu respuesta con g para λ = 40°.



84. Un protón en un sincrotrón se mueve en un círculo de radio 1 km y aumenta su velocidad en v(t) = c₁ + c₂t², donde c₁ = 2.0 × 10⁵ m/s, c₂ = 10⁵ m/s³. (a) ¿Cuál es la aceleración total del protón en t = 5.0 s? (b) ¿A qué hora la expresión de la velocidad se vuelve no física?

85. Una pala de hélice en reposo comienza a girar desde t = 0 s hasta t = 5.0 s con una aceleración tangencial de la punta de la cuchilla a 3.00 m/s². La punta de la cuchilla está a 1,5 m del eje de rotación. En t = 5.0 s, ¿cuál es la aceleración total de la punta de la cuchilla?

86. Una partícula está ejecutando un movimiento circular con una frecuencia angular constante de ω = 4.00 rad/s. Si el tiempo t = 0 corresponde a la posición de la partícula en y = 0 m y x = 5 m, (a) ¿cuál es la posición de la partícula en t = 10 s? (b) ¿Cuál es su velocidad en este momento? (c) ¿Cuál es su aceleración?

87. La aceleración centrípeta de una partícula es a_C = 4.0 m/s² en t = 0 s. Está ejecutando un movimiento circular uniforme sobre un eje a una distancia de 5.0 m. ¿Cuál es su velocidad en t = 10 s?

88. Una varilla de 3,0 m de longitud gira a 2,0 rev/s alrededor de un eje en un extremo. Compare las aceleraciones centrípetas en radios de (a) 1.0 m, (b) 2.0 m, y (c) 3.0 m.

89. Una partícula ubicada inicialmente en (1.5j + 4.0k) m (1.5j ^ + 4.0k ^) m sufre un desplazamiento de (2.5i + 3.2j-1.2k) m. (2.5i ^ + 3.2j ^ - 1.2k ^) m. ¿Cuál es la posición final de la partícula? 90. La posición de una partícula está dada por r→(t) = (50 m/s)ti^ - (4.9 m/s²)t²j^. (a) ¿Cuál es la velocidad y la aceleración de la partícula como funciones del tiempo? (b) ¿Cuáles son las condiciones iniciales para producir el movimiento?

91. Una nave espacial viaja a una velocidad constante de v→(t) = 250.0i^ m/s cuando sus cohetes disparan, dándole una aceleración de a→(t) = (3.0i^ + 4.0k^) m/s². ¿Cuál es su velocidad 55 s después del disparo de los cohetes?

92. Una ballesta se dirige horizontalmente a un objetivo a 40 m de distancia. La flecha golpea 30 cm debajo del punto al cual fue apuntada. ¿Cuál es la velocidad inicial de la flecha?

93. Un saltador de longitud puede saltar una distancia de 8.0 m cuando despega en un ángulo de 45° con respecto a la horizontal. Suponiendo que puede saltar con la misma velocidad inicial en todos los ángulos, ¿cuánta distancia pierde al despegar a 30°?

94. En el planeta Arcon, el alcance horizontal máximo de un proyectil lanzado a 10 m/s es de 20 m. ¿Cuál es la aceleración de la gravedad en este planeta?

95. Un ciclista de montaña se encuentra con un salto en un hipódromo que lo envía al aire a 60° de la horizontal. Si aterriza a una distancia horizontal de 45.0 m y 20 m por debajo de su punto de lanzamiento, ¿cuál es su velocidad inicial?

96. ¿Cuál tiene la mayor aceleración centrípeta, un automóvil con una velocidad de 15,0 m/s a ​​lo largo de una pista circular de radio 100,0 m o un automóvil con una velocidad de 12,0 m/s a ​​lo largo de una pista circular de radio de 75,0 m?

97. Un satélite geosincrónico orbita la Tierra a una distancia de 42,250.0 km y tiene un período de 1 día. ¿Cuál es la aceleración centrípeta del satélite?

98. Dos lanchas rápidas viajan a la misma velocidad con respecto al agua en direcciones opuestas en un río en movimiento. Un observador en la orilla del río ve los botes moviéndose a 4.0 m/s y 5.0 m/s. (a) ¿Cuál es la velocidad de los barcos en relación con el río? (b) ¿Qué tan rápido se mueve el río en relación con la orilla?

Problemas reto

99. El par más largo del mundo 3. El tee del par 3 más largo del mundo se encuentra sobre la montaña Hanglip de Sudáfrica a 400.0 m sobre el green y solo se puede llegar en helicóptero. La distancia horizontal al green es 359.0 m. Desprecia la resistencia del aire y responde las siguientes preguntas. (a) Si un golfista lanza un tiro que es de 40° con respecto a la horizontal, ¿qué velocidad inicial debe darle a la pelota? (b) ¿Cuál es el tiempo para llegar al green?

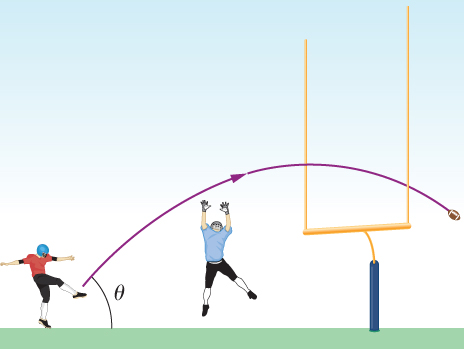
100. Cuando un pateador de futbol de campo patea una pelota lo más fuerte que puede a 45° de la horizontal, la pelota acaba por despejar el travesaño de 3 m de altura de la portería a 45,7 m de distancia. (a) ¿Cuál es la velocidad máxima que el pateador puede impartir al fútbol? (b) Además de despejar el travesaño, el balón debe estar lo suficientemente alto en el aire temprano durante su vuelo para despejar el alcance del liniero defensivo. Si el liniero está a 4,6 m de distancia y tiene un alcance vertical de 2,5 m, ¿puede bloquear el intento de gol de campo de 45,7 m? (c) ¿Qué pasa si el liniero está a 1.0 m de distancia?



101. Un camión viaja hacia el este a 80 km/h. En una intersección a 32 km adelante, un automóvil viaja hacia el norte a 50 km/h. (a) ¿Cuánto tiempo después de este momento los vehículos estarán más cerca el uno del otro? (b) ¿Qué tan separados estarán en ese punto?