Preguntas y problemas - Capítulo III

Preguntas conceptuales

3.2 Posición, desplazamiento y velocidad promedio

1. Da un ejemplo en el que haya claras diferencias entre la distancia recorrida, el desplazamiento y la magnitud del desplazamiento. Identifica cada cantidad en tu ejemplo específicamente.

2. ¿Bajo qué circunstancias la distancia recorrida es igual a la magnitud del desplazamiento? ¿Cuál es el único caso en el que la magnitud del desplazamiento y el desplazamiento son exactamente iguales?

3. Las bacterias se mueven hacia adelante y hacia atrás usando sus flagelos (estructuras que parecen pequeñas colas). Se han observado velocidades de hasta 50 μm/s (50 × 10^-6 m/s). La distancia total recorrida por una bacteria es grande para su tamaño, mientras que su desplazamiento es pequeño. ¿Por qué es esto?

4. Da un ejemplo de un dispositivo utilizado para medir el tiempo e identifica qué cambio en ese dispositivo indica un cambio en el tiempo.

5. ¿El odómetro de un automóvil mide la distancia recorrida o el desplazamiento?

6. Durante un intervalo de tiempo dado, la velocidad promedio de un objeto es cero. ¿Qué puedes decir sobre su desplazamiento en el intervalo de tiempo?

3.3 Velocidad instantánea y Rapidez

7. Hay una distinción entre la rapidez promedio y la magnitud de la velocidad promedio. Da un ejemplo que ilustre la diferencia entre estas dos cantidades.

8. ¿El velocímetro de un automóvil mide rapidez o velocidad?

9. Si divides la distancia total recorrida en un viaje en automóvil (según lo determinado por el cuentakilómetros) por el tiempo transcurrido del viaje, ¿estás calculando la rapidez promedio o la magnitud de la velocidad promedio? ¿Bajo qué circunstancias son estas dos cantidades iguales?

10. ¿Cómo se relacionan la velocidad instantánea y la rapidez instantánea entre sí? ¿Cómo difieren?

3.4 Aceleración promedio e instantánea

11. ¿Es posible que la rapidez sea constante mientras que la aceleración no es cero?

12. ¿Es posible que la velocidad sea constante mientras que la aceleración no es cero? Explica.

13. Da un ejemplo en el que la velocidad es cero pero la aceleración no.

14. Si un tren subterráneo se mueve hacia la izquierda (tiene una velocidad negativa) y luego se detiene, ¿cuál es la dirección de su aceleración? ¿La aceleración es positiva o negativa?

15. Los signos más y menos se usan en movimiento unidimensional para indicar la dirección. ¿Cuál es el signo de una aceleración que reduce la magnitud de una velocidad negativa? y ¿de una velocidad positiva?

3.5 Movimiento uniformemente acelerado

16. Al analizar el movimiento simple de un objeto, ¿cuál es el número de variables físicas conocidas que se necesitan para resolver las cantidades desconocidas usando las ecuaciones cinemáticas?

17. Indica dos escenarios de la cinemática de un solo objeto donde tres cantidades conocidas requieren dos ecuaciones cinemáticas para resolver las incógnitas.

3.6 Caida libre

18. ¿Cuál es la aceleración de una roca lanzada hacia arriba en el camino hacia arriba? En la cima de su vuelo? ¿Cuesta abajo? Supón que no hay resistencia al aire.

19. Un objeto que se lanza hacia arriba cae a la Tierra. Este es un movimiento unidimensional. (a) ¿Cuándo es su velocidad cero? (b) ¿Su velocidad cambia de dirección? (c) ¿La aceleración tiene el mismo signo en el camino ascendente que en el descenso?

20. Supongamos que arrojas una roca casi recta hacia un coco en una palmera y la roca no toca el coco en el camino hacia arriba, pero lo golpea en el camino hacia abajo. Despreciando la resistencia del aire y la ligera variación horizontal en movimiento, ¿cómo se compara la velocidad de la roca si hubiése golpeado el coco en el camino en la subida con el de bajada? ¿Es más probable tumbar el coco en el camino hacia arriba o hacia abajo? Explica.

21. La gravedad de una caída depende de tu velocidad cuando tocas el suelo. ¿cuántas veces más alto podrías caer de manera segura en la Luna que en la Tierra (la aceleración de la gravedad en la Luna es aproximadamente una sexta parte de la de la Tierra)?

22. ¿Cuántas veces más alto puede saltar un astronauta en la Luna que en la Tierra si su velocidad de despegue es la misma en ambos lugares (la aceleración de la gravedad en la Luna es aproximadamente la sexta parte de la de la Tierra)?

3.7 Encontrando la velocidad y el desplazamiento a partir de la aceleración

23. Cuando se te da la función de aceleración, ¿qué información adicional se necesita para encontrar la función de velocidad y la función de posición?

Problemas

3.2 Posición, desplazamiento y velocidad promedio

24. Considera un sistema de coordenadas en el que el eje x positivo se dirige verticalmente hacia arriba. ¿Cuáles son las posiciones de una partícula (a) 5.0 m directamente sobre el origen y (b) 2.0 m debajo del origen?

25. Un automóvil está a 2.0 km al oeste de un semáforo en t = 0 y 5.0 km, al este del semáforo en t = 6.0 min. Supón que el origen del sistema de coordenadas es el semáforo y la dirección x positiva es hacia el este. (a) ¿Cuáles son los vectores de posición del automóvil en estas dos ocasiones? (b) ¿Cuál es el desplazamiento del automóvil entre 0 min y 6.0 min?

26. El tren maglev de Shanghai conecta Longyang Road con el aeropuerto internacional de Pudong, a una distancia de 30 km. El viaje dura 8 minutos en promedio. ¿Cuál es la velocidad promedio del tren de levitación magnética?

27. La posición de una partícula que se mueve a lo largo del eje x viene dada por x(t) = 4.0 - 2.0t m. (a) ¿A qué hora la partícula cruza el origen? (b) ¿Cuál es el desplazamiento de la partícula entre t = 3.0s y t = 6.0s?

28. Un ciclista recorre 8.0 km al este durante 20 minutos, luego gira y se dirige hacia el oeste durante 8 minutos y 3.2 km. Finalmente, corre hacia el este durante 16 km, lo que demora 40 minutos. (a) ¿Cuál es el desplazamiento final del ciclista? (b) ¿Cuál es su velocidad promedio?

29. El 15 de febrero de 2013, un meteorito superbolídeo (más brillante que el Sol) entró en la atmósfera terrestre sobre Chelyabinsk, Rusia, y explotó a una altitud de 23.5 km. Los testigos pudieron sentir el intenso calor de la bola de fuego, y la onda expansiva de la explosión hizo saltar las ventanas de los edificios. La onda expansiva tardó aproximadamente 2 minutos y 30 segundos en alcanzar el nivel del suelo. (a) ¿Cuál fue la velocidad promedio de la onda expansiva? b) Compare esto con la velocidad del sonido, que es de 343 m/s al nivel del mar.

3.3 Velocidad instantánea y Rapidez

30. Una marmota corre 20 m hacia la derecha en 5 s, luego gira y corre 10 m hacia la izquierda en 3 s. (a) ¿Cuál es la velocidad promedio de la marmota? (b) ¿Cuál es su rapidez promedio?

31. Dibuja el gráfico de velocidad versus tiempo a partir del siguiente gráfico de posición versus tiempo.



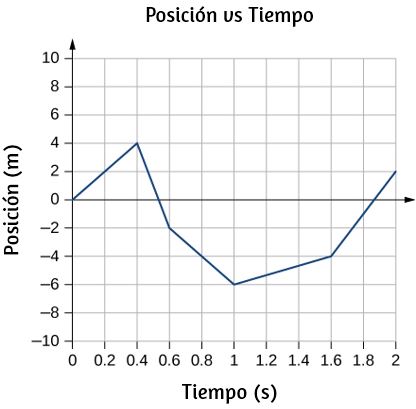
32. Dibuje el gráfico de velocidad versus tiempo a partir del siguiente gráfico de posición versus tiempo.



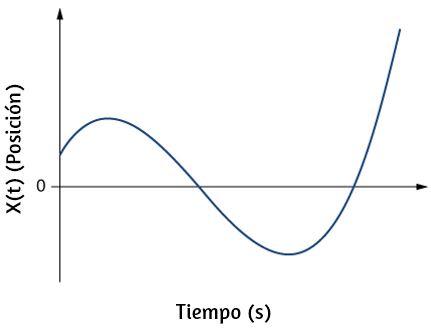
33. Dado el siguiente gráfico de velocidad versus tiempo, dibuje el gráfico de posición versus tiempo.



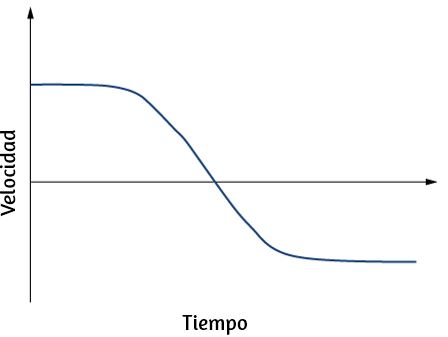
34. Un objeto tiene una función de posición x(t) = 5t m. (a) ¿Cuál es la velocidad en función del tiempo? (b) Grafica la función de posición y la función de velocidad.

35. Una partícula se mueve a lo largo del eje x de acuerdo con x(t) = 10t - 2t²m. (a) ¿Cuál es la velocidad instantánea en t = 2 s y t = 3 s? (b) ¿Cuál es la rapidez instantánea en estos momentos? (c) ¿Cuál es la velocidad promedio entre t = 2 s y t = 3 s?

36. Resultados irrazonables. Una partícula se mueve a lo largo del eje x de acuerdo con x(t) = 3t³ + 5t. ¿A qué hora es la velocidad de la partícula igual a cero? Es esto razonable?

3.4 Aceleración promedio e instantánea

37. Un guepardo puede acelerar desde el descanso hasta una velocidad de 30.0 m/s en 7.00 s. ¿Cuál es su aceleración?

38. El Dr. John Paul Stapp fue un oficial de la Fuerza Aérea de los EE. UU. Que estudió los efectos de la aceleración extrema en el cuerpo humano. El 10 de diciembre de 1954, Stapp montó un trineo cohete, acelerando desde el reposo hasta una velocidad máxima de 282 m/s (1015 km/h) en 5,00 s y fue detenido bruscamente en solo 1,40 s. Calcula su (a) aceleración en su dirección de movimiento y (b) aceleración opuesta a su dirección de movimiento. Expresa cada uno en múltiplos de g (9.80 m/s²) tomando su relación a la aceleración de la gravedad.

39. Dibuja el gráfico de aceleración versus tiempo a partir del siguiente gráfico de velocidad versus tiempo.



40. Una persona que viaja hacia atrás hace retroceder su auto fuera de su garaje con una aceleración de 1.40 m/s². (a) ¿Cuánto tiempo le toma alcanzar una velocidad de 2.00 m/s? (b) Si luego frena en 0.800 s, ¿cuál es su aceleración?

41. Supón que un misil balístico intercontinental pasa del reposo a una velocidad suborbital de 6.50 km/s en 60.0 s (la velocidad y el tiempo reales son clasificados). ¿Cuál es su aceleración promedio en metros por segundo y en múltiplos de g (9.80 m/s²)?

42. Un avión, comenzando desde el reposo, se mueve por la pista a una aceleración constante durante 18 s y luego despega a una velocidad de 60 m/s. ¿Cuál es la aceleración promedio del avión?

3.5 Movimiento uniformemente acelerado

43. Una partícula se mueve en línea recta a una velocidad constante de 30 m/s. ¿Cuál es su desplazamiento entre t = 0 y t = 5.0 s?

44. Una partícula se mueve en línea recta con una velocidad inicial de 30 m/s y una aceleración constante de 30 m/s². Si en t = 0, x = 0 y v = 0, ¿cuál es la posición de la partícula en t = 5 s?

45. Una partícula se mueve en línea recta con una velocidad inicial de 30 m/s y una aceleración constante de 30 m/s². (a) ¿Cuál es su desplazamiento en t = 5 s? (b) ¿Cuál es su velocidad en este mismo momento?

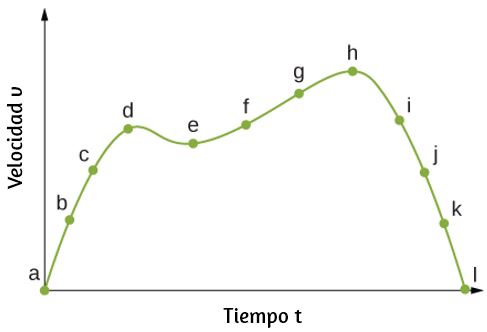
46. (a) Dibuja un gráfico de la velocidad en función del tiempo correspondiente a la gráfica del desplazamiento en función del tiempo que se muestra en la siguiente figura. (b) Identifica la hora u horas (t_a, t_b, t_c, etc.) en que la velocidad instantánea tiene el mayor valor positivo. (c) ¿En qué momentos es cero? (d) ¿En qué momentos es negativo?



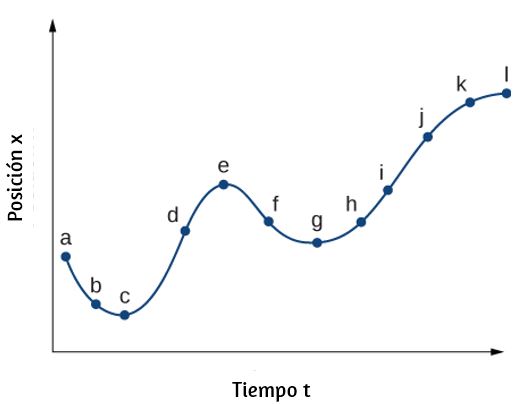
47. (a) Dibuja un gráfico de la aceleración vs tiempo correspondiente al gráfico de velocidad vs tiempo que se da en la siguiente figura. (b) Identifica la hora u horas (t_a, t_b, t_c, etc.) en las cuales la aceleración tiene el mayor valor positivo. (c) ¿En qué momentos es cero? (d) ¿En qué momentos es negativo?



48. Una partícula tiene una aceleración constante de 6.0 m/s². (a) Si su velocidad inicial es de 2.0 m/s, ¿a qué hora es su desplazamiento de 5.0 m? (b) ¿Cuál es su velocidad en ese momento?

49. En t = 10 s, una partícula se mueve de izquierda a derecha con una velocidad de 5.0 m/s. En t = 20 s, la partícula se mueve de derecha a izquierda con una velocidad de 8.0 m/s. Suponiendo que la aceleración de la partícula es constante, determina (a) su aceleración, (b) su velocidad inicial, y (c) el instante en que su velocidad es cero.

50. Una pelota bien lanzada queda atrapada en un guante bien acolchado. Si la aceleración de la bola es 2.10 × 10⁴ m/s², y 1.85 ms (1 ms = 10^-3 s) transcurre desde el momento en que la pelota toca el guante por primera vez hasta que se detiene , ¿cuál es la velocidad inicial de la pelota?

51. Una bala en una pistola se acelera desde la cámara de disparo hasta el extremo del barril a una velocidad promedio de 6.20 × 10⁵ m/s², para 8.10 × 10^-4 s ¿Cuál es la velocidad en la boca del arma (es decir, su velocidad final)?

52. a) Un tren de cercanías acelera a razón de 1,35 m/s². ¿Cuánto tiempo lleva alcanzar su velocidad máxima de 80.0 km/h, comenzando desde el reposo? (b) El mismo tren ordinariamente desacelera a una velocidad de 1.65 m/s². ¿Cuánto tiempo demora en detenerse desde su velocidad máxima? (c) En emergencias, el tren puede desacelerarse más rápidamente, llegando a parar desde 80.0 km/h en 8.30 s. ¿Cuál es su aceleración de emergencia en metros por segundo al cuadrado?

53. Al ingresar a una autopista, un automóvil acelera desde el reposo a una velocidad de 2.04 m/s² durante 12.0 s. (a) Dibuja un boceto de la situación. (b) Enumera los datos conocidos en este problema. (c) ¿Qué distancia recorre el automóvil en esos 12.0 s? Para resolver esta parte, primero identifica los datos desconocidos, luego indica cómo elegiste la ecuación apropiada para resolverlo. Después de elegir la ecuación, muestra tus pasos para hallar los datos desconocidos, verifica sus unidades y debate si la respuesta es razonable. (d) ¿Cuál es la velocidad final del automóvil? Resuelve para este dato desconocido de la misma manera que en (c), mostrando todos los pasos explícitamente.

54. Resultados irrazonables. Al final de una carrera, un corredor desacelera desde una velocidad de 9.00 m/s a ​​una rata de 2.00 m/s². (a) ¿Cuánto viaja en los próximos 5.00 s? (b) ¿Cuál es su velocidad final? (c) Evalúa el resultado. ¿Tiene sentido?

55. La sangre se acelera desde el reposo hasta 30.0 cm/s en una distancia de 1.80 cm por el ventrículo izquierdo del corazón. (a) Haz un boceto de la situación. (b) Enumera los datos conocidos en este problema. (c) ¿Cuánto tiempo demora la aceleración? Para resolver esta parte, primero identifica los datos desconocidos, luego analiza cómo elegiste la ecuación adecuada para resolverlo. Después de elegir la ecuación, muestra tus pasos para hallar los datos desconocidos y verifica tus unidades. (d) ¿Es la respuesta razonable en comparación con el tiempo de un latido del corazón?

56. En una cachetada, un jugador de hockey acelera el disco desde una velocidad de 8.00 m/s a 40.0 m/s en la misma dirección. Si esta tarda 3.33 × 10^-2 s, ¿cuál es la distancia a la que acelera el disco?

57. Una motocicleta poderosa puede acelerar desde el reposo hasta 26.8 m/s (100 km/h) en solo 3.90 s. (a) ¿Cuál es su aceleración promedio? (b) ¿Qué tan lejos viaja en ese momento?

58. Los trenes de carga solo pueden producir aceleraciones relativamente pequeñas. (a) ¿Cuál es la velocidad final de un tren de carga que acelera a una velocidad de 0.0500 m/s² durante 8.00 min, comenzando con una velocidad inicial de 4.00 m/s? (b) Si el tren puede reducir la velocidad a una rata de 0.550 m/s², ¿cuánto tiempo tardará en detenerse a partir de esta velocidad? (c) ¿Qué tan lejos viajará en cada caso?

59. Un proyectil de fuegos artificiales se acelera desde el reposo a una velocidad de 65.0 m/s en una distancia de 0.250 m. (a) Calcula la aceleración. (b) ¿En cuánto se obtiene la aceleración?

60. Un cisne en un lago se pone en el aire aleteando y corriendo sobre el agua. (a) Si el cisne debe alcanzar una velocidad de 6.00 m/s para despegar y acelera desde el reposo a una velocidad promedio de 0.35 m/s², ¿cuán lejos viajará antes de despegar? (b) ¿Cuánto tiempo lleva esto?

61. El cerebro de un pájaro carpintero está especialmente protegido de grandes aceleraciones por las uniones de un tendón dentro del cráneo. Mientras picotea en un árbol, la cabeza del pájaro carpintero se detiene desde una velocidad inicial de 0.600 m/s a ​​una distancia de solo 2.00 mm. (a) Encuentra la aceleración en metros por segundo al cuadrado y en múltiplos de g, donde g = 9.80 m/s². (b) Calcula el tiempo de parada. (c) Los tendones que acunan el cerebro se estiran, haciendo que su distancia de detención sea de 4.50 mm (mayor que la cabeza y, por lo tanto, menor aceleración del cerebro). ¿Cuál es la aceleración del cerebro, expresada en múltiplos de g?

62. Un jugador de fútbol desprevenido choca con un poste acolchado mientras corre a una velocidad de 7.50 m/s y se detiene por completo después de comprimir el acolchado y su cuerpo 0.350 m. (a) ¿Cuál es su aceleración? (b) ¿Cuánto dura la colisión?

63. Un paquete sanitario se deja caer de un avión de carga y aterriza en el bosque. Si suponemos que la velocidad del paquete sanitario, en caso de impacto, es de 54 m/s (123 mph), entonces, ¿cuál es su aceleración? Supongamos que los árboles y la nieve lo detienen a una distancia de 3.0 m.

64. Un tren expreso pasa por una estación. Entra con una velocidad inicial de 22.0 m/s y desacelera a una rata de 0.150 m/s² a medida que avanza. La estación mide 210.0 m de largo. (a) ¿Qué tan rápido va cuando la nariz sale de la estación? (b) ¿Cuánto mide la nariz del tren en la estación? (c) Si el tren tiene 130 m de largo, ¿cuál es la velocidad de la cola del tren cuando sale? (d) ¿Cuándo sale la cola del tren de la estación?

65. Resultados irrazonables. Los dragsters en realidad pueden alcanzar una velocidad máxima de 145.0 m/s en solo 4.45 s. (a) Calcula la aceleración promedio para un dragster. (b) Encuentra la velocidad final de este dragster comenzando desde el reposo y acelerando a la velocidad encontrada en (a) por 402.0 m (un cuarto de milla) sin usar ninguna información a tiempo. (c) ¿Por qué la velocidad final es mayor que la utilizada para encontrar la aceleración promedio? (Sugerencia: Considere si la suposición de la aceleración constante es válida para un dragster. De lo contrario, analice si la aceleración sería mayor al principio o al final de la carrera y qué efecto tendría sobre la velocidad final).

3.6 Caida libre

66. Calcula el desplazamiento y la velocidad en los momentos de (a) 0.500 s, (b) 1.00 s, (c) 1.50 s, y (d) 2.00 s para una pelota lanzada hacia arriba con una velocidad inicial de 15.0 m/s. Toma el punto de lanzamiento con y⁰ = 0.

67. Calcula el desplazamiento y la velocidad en tiempos de (a) 0.500 s, (b) 1.00 s, (c) 1.50 s, (d) 2.00 s, y (e) 2.50 s para una roca arrojada directamente hacia abajo con una velocidad inicial de 14.0 m/s desde el Puente Verrazano Narrows en la ciudad de Nueva York. La carretera de este puente está a 70.0 m sobre el nivel del agua.

68. Un árbitro de básquetbol tira el balón hacia arriba para el inicio del partido. ¿A qué velocidad debe un jugador de baloncesto dejar la tierra para elevarse 1.25 m por encima del suelo en un intento de obtener la pelota?

69. Un helicóptero de rescate está sobrevolando a una persona cuyo bote se ha hundido. Uno de los rescatadores arroja un salvavidas directo a la víctima con una velocidad inicial de 1.40 m/s y observa que tarda 1,8 s en llegar al agua. (a) Enumere los datos conocidos en este problema. (b) ¿Qué tan alto sobre el agua se lanzó el salvavidas? Ten en cuenta que la corriente descendente del helicóptero reduce los efectos de la resistencia del aire sobre el salvavidas que cae, por lo que una aceleración igual a la de la gravedad es razonable.

70. Resultados irrazonables Un delfín en un espectáculo acuático salta directamente fuera del agua a una velocidad de 15.0 m/s. (a) Enumera los datos conocidos en este problema. (b) ¿Qué tan alto se eleva su cuerpo sobre el agua? Para resolver esta parte, primero nota que la velocidad final es ahora conocida e identifica su valor. Luego, identifica los datos desconocidos y analiza cómo elegiste la ecuación adecuada para resolverlo. Después de elegir la ecuación, muestra tus pasos para hallar el dato desconocido, verifica las unidades y debate si la respuesta es razonable. (c) ¿Cuánto tiempo está el delfín en el aire? Desprecia cualquier efecto resultante de su tamaño u orientación.

71. Un buceador rebota hacia arriba desde un trampolín, evitando el trampolín al bajar, y cae de pies en una piscina. El comienza con una velocidad de 4.00 m/s y su punto de despegue es 1.80 m por encima de la piscina. (a) ¿Cuál es su punto más alto por encima del trampolín? (b) ¿Cuánto tiempo llevan sus pies en el aire? (c) ¿Cuál es su velocidad cuando sus pies tocan el agua?

72. (a) Calcula la altura de un acantilado si tardan 2,35 s para que una roca golpee el suelo cuando se lanza directamente hacia arriba desde el acantilado con una velocidad inicial de 8.00 m/s. (b) ¿Cuánto tiempo llevaría alcanzar el suelo si se lanza directamente hacia abajo con la misma velocidad?

73. Un golfista de tiro muy fuerte, pero inepto, pone el tiro recto verticalmente con una velocidad inicial de 11.0 m/s. ¿Cuánto tiempo tiene para salir del camino si el lanzamiento fue lanzado a una altura de 2.20 m y tiene 1.80 m de altura?

74. Lanzas una bola hacia arriba con una velocidad inicial de 15,0 m/s. Pasa una rama de árbol en el camino hacia arriba a una altura de 7.0 m. ¿Cuánto tiempo adicional transcurre antes de que la pelota pase por la rama del árbol en el camino de regreso?

75. Un canguro puede saltar sobre un objeto de 2,50 m de altura. (a) Considerando solo su movimiento vertical, calcula su velocidad vertical cuando abandona el suelo. (b) ¿Cuánto tiempo está en el aire?

76. Parado en la base de uno de los acantilados del monte Arapiles en Victoria, Australia, un excursionista oye el desprendimiento de una roca desde una altura de 105.0 m. No puede ver la roca de inmediato, pero luego lo hace, 1.50 s después. (a) ¿Qué tan arriba del excursionista está la roca cuando puede verla? (b) ¿Cuánto tiempo tiene para moverse antes de que la roca golpee su cabeza?

77. Hay un acantilado de 250 m de altura en Half Dome en el Parque Nacional Yosemite en California. Supongamos que una roca se suelta desde lo alto de este acantilado. (a) ¿Qué tan rápido irá cuando toque el suelo? (b) Suponiendo un tiempo de reacción de 0.300 s, ¿cuánto tiempo tendrá que apartarse un turista en la parte inferior después de escuchar el sonido de la roca al romperse (despreciando la altura del turista, que de todos modos se volvería insignificante? si es golpeado)? La velocidad del sonido es 335.0 m/s en este día.

3.7 Encontrando la velocidad y el desplazamiento a partir de la aceleración

78. La aceleración de una partícula varía con el tiempo de acuerdo con la ecuación a (t) = pt² - qt³. Inicialmente, la velocidad y la posición son cero. (a) ¿Cuál es la velocidad en función del tiempo? (b) ¿Cuál es la posición en función del tiempo?

79. Entre t = 0 y t = t₀, un cohete se mueve hacia arriba con una aceleración dada por a(t) = A - Bt^1/2, donde A y B son constantes. (a) Si x está en metros y t en segundos, ¿cuáles son las unidades de A y B? (b) Si el cohete comienza desde el reposo, ¿cómo varía la velocidad entre t = 0 y t = t₀? (c) Si su posición inicial es cero, ¿cuál es la posición del cohete en función del tiempo durante este mismo intervalo de tiempo?

80. La velocidad de una partícula que se mueve a lo largo del eje x varía con el tiempo según la función v(t) = A + B^-1, donde A = 2 m/s, B = 0.25 m y 1.0s ≤ t ≤ 8.0s. Determina la aceleración y la posición de la partícula en t = 2.0 s y t = 5.0 s. Supón que x(t = 1s) = 0.

81. Una partícula en reposo deja el origen con su velocidad que aumenta con el tiempo según v(t) = 3.2t m/s. En 5.0 s, la velocidad de la partícula comienza a disminuir de acuerdo con [16.0 - 1.5(t - 5.0)] m/s. Esta disminución continúa hasta t = 11.0 s, después de lo cual la velocidad de la partícula permanece constante a 7.0 m/s. (a) ¿Cuál es la aceleración de la partícula como una función del tiempo? (b) ¿Cuál es la posición de la partícula en t = 2.0 s, t = 7.0 s, y t = 12.0 s?

Problemas adicionales

82. El jugador profesional de béisbol Nolan Ryan podría lanzar una pelota de béisbol a aproximadamente 160.0 km/h. A esa velocidad promedio, ¿cuánto tiempo le tomó a Ryan lanzar una pelota para llegar al plato de home, que está a 18.4 m del montículo del pitcher? Compare esto con el tiempo de reacción promedio de un humano a un estímulo visual, que es 0.25 s.

83. Un avión sale de Chicago y realiza el viaje de 3000 km a Los Ángeles en 5.0 h. Un segundo avión sale de Chicago media hora más tarde y llega a Los Ángeles al mismo tiempo. Compara las velocidades promedio de los dos aeroplanos. Ignora la curvatura de la Tierra y la diferencia de altitud entre las dos ciudades.

84. Resultados irrazonables. Un ciclista recorre 16.0 km al este, luego 8.0 km al oeste, luego 8.0 km al este, luego 32.0 km al oeste, y finalmente a 11.2 km al este. Si su velocidad promedio es de 24 km/h, ¿cuánto tiempo tardó en completar el viaje? ¿Es este un tiempo razonable?

85. Un objeto tiene una aceleración de + 1.2 cm/s². En t = 4.0s, su velocidad es -3.4cm/s. Determina las velocidades del objeto en t = 1.0 s y t = 6.0 s.

86. Una partícula se mueve a lo largo del eje x de acuerdo con la ecuación x(t) = 2.0 -4.0t² m. ¿Cuál es la velocidad y la aceleración en t = 2.0 s y t = 5.0 s?

87. Una partícula que se mueve a aceleración constante tiene velocidades de 2.0 m/s² en t = 2.0 s y -7.6 m/s en t = 5.2 s. ¿Cuál es la aceleración de la partícula?

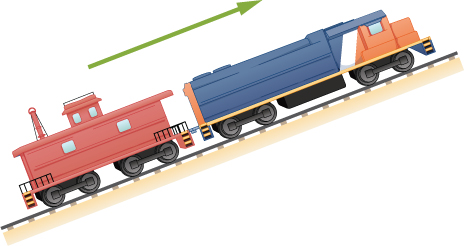
88. Un tren está subiendo una pendiente pronunciada a velocidad constante (ver la siguiente figura) cuando su vagón se suelta y comienza a rodar libremente a lo largo de la vía. Después de 5.0 s, el furgón de cola está a 30 m detrás del tren. ¿Cuál es la aceleración del furgón de cola?



89. Un electrón se mueve en línea recta con una velocidad de 4.0 × 10⁵ m/s. Entra en una región de 5,0 cm de largo donde sufre una aceleración de 6.0 × 10¹² m/s² a lo largo de la misma línea recta. (a) ¿Cuál es la velocidad del electrón cuando emerge de esta región? b) ¿Cuánto tiempo tarda el electrón en cruzar la región?

90. Un conductor de ambulancia está llevando un paciente al hospital. Mientras viaja a 72 km/h, se da cuenta de que el semáforo en las próximas intersecciones se ha vuelto amarillo. Para llegar a la intersección antes de que la luz se vuelva roja, debe viajar 50 m en 2.0 s. (a) ¿Qué aceleración mínima debe tener la ambulancia para llegar a la intersección antes de que la luz se vuelva roja? (b) ¿Cuál es la velocidad de la ambulancia cuando llega a la intersección?

91. Una motocicleta que se está desacelerando uniformemente cubre 2.0 kilómetros sucesivos en 80 s y 120 s, respectivamente. Calcula (a) la aceleración de la motocicleta y (b) su velocidad al comienzo y al final del viaje de 2 km.

92. Un ciclista viaja del punto A al punto B en 10 min. Durante los primeros 2.0 minutos de su viaje, mantiene una aceleración uniforme de 0.090 m/s². Luego viaja a velocidad constante durante los siguientes 5.0 min. Luego, desacelera a un ritmo constante para detenerse en el punto B 3.0 minutos más tarde. (a) Dibuja el gráfico de velocidad versus tiempo para el viaje. (b) ¿Cuál es la aceleración durante los últimos 3 minutos? (c) ¿Cuánto viaja el ciclista?

93. Dos trenes se mueven a 30 m/s en direcciones opuestas en la misma pista. Los ingenieros ven simultáneamente que están en curso de colisión y aplican los frenos cuando están a 1000 m de distancia. Suponiendo que ambos trenes tienen la misma aceleración, ¿cuánto debe ser esta aceleración si los trenes se detienen justo antes de colisionar?

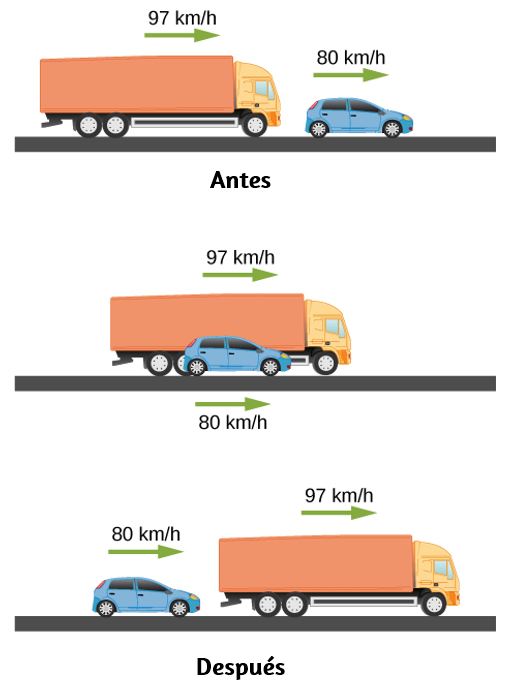
94. Un camión de 10.0 m de largo que se mueve con una velocidad constante de 97.0 km/h pasa un automóvil de 3.0 m de largo que se mueve con una velocidad constante de 80.0 km/h. ¿Cuánto tiempo transcurre entre el momento en que la parte delantera del camión está nivelada con la parte posterior del automóvil y el momento en que la parte trasera del camión está nivelada con la parte delantera del automóvil?



95. Un coche de policía espera escondido ligeramente fuera de la carretera. El automóvil de la policía detecta un automóvil que circula a una velocidad de 40 m/s. En el instante en que el automóvil que circula a alta velocidad pasa el automóvil de la policía, éste acelera desde el reposo a 4 m/s² para atrapar el automóvil que circula a gran velocidad. ¿Cuánto tiempo le toma al carro de la policía atrapar el automóvil que circula a alta velocidad?

96. Pablo corre en una media maratón a una velocidad de 3 m/s. Otro corredor, Jacob, está 50 metros detrás de Pablo con la misma velocidad. Jacob comienza a acelerar a 0.05 m/s². (a) ¿Cuánto le lleva a Jacob alcanzar a Pablo? (b) ¿Cuál es la distancia cubierta por Jacob? (c) ¿Cuál es la velocidad final de Jacob?

97. Resultados irrazonables. Un corredor se acerca a la línea de meta y está a 75 m de distancia; su velocidad promedio en esta posición es de 8 m/s. El corredor desacelera en este punto a 0.5 m/s². ¿Cuánto tiempo le lleva cruzar la línea de meta desde 75 m de distancia? ¿Es esto razonable?

98. Un avión acelera a 5.0 m/s² durante 30.0 s. Durante este tiempo, cubre una distancia de 10.0 km. ¿Cuáles son las velocidades inicial y final del avión?

99. Compara la distancia recorrida de un objeto que experimenta un cambio en la velocidad que es dos veces su velocidad inicial con un objeto que cambia su velocidad cuatro veces su velocidad inicial durante el mismo período de tiempo. Las aceleraciones de ambos objetos son constantes.

100. Un objeto se mueve hacia el este con una velocidad constante y está en la posición x₀ en t₀ = 0. (a) ¿Con qué aceleración debe estar el objeto para que su desplazamiento total sea cero en un momento posterior t? (b) ¿Cuál es la interpretación física de la solución en el caso de t → ∞?

101. Una pelota se lanza hacia arriba. Pasa una ventana de 2.00 m de altura a 7.50 m del suelo en su trayectoria ascendente y tarda 1.30 s en pasar la ventana. ¿Cuál fue la velocidad inicial de la pelota?

102. Se arroja una moneda desde un globo de aire caliente que se encuentra a 300 m sobre el nivel del suelo y se eleva a 10.0 m/s hacia arriba. Para la moneda, encuentra (a) la altura máxima alcanzada, (b) su posición y velocidad 4.00 s después de ser soltada, y (c) el tiempo antes de que toque el suelo.

103. Una pelota de tenis se deja caer sobre un piso duro desde una altura de 1,50 m y rebota a una altura de 1,10 m. (a) Calcula su velocidad justo antes de que golpee el piso. (b) Calcula su velocidad justo después de que abandona el piso en su camino de regreso. (c) Calcula su aceleración durante el contacto con el piso si ese contacto dura 3.50 ms (3.50 × 10^-3 s) (d) ¿Cuánto se comprimió la pelota durante su colisión con el piso, asumiendo que el piso es absolutamente rígido?

104. Resultados irrazonables. Una gota de lluvia cae de una nube a 100 m del suelo. Desprecia la resistencia del aire. ¿Cuál es la velocidad de la gota de agua cuando toca el suelo? ¿Es este un número razonable?

105. Compara el tiempo en el aire de un jugador de básquetbol que salta 1.0 m verticalmente del suelo con el de un jugador que salta 0.3 m verticalmente.

106. Supongamos que una persona tarda 0.5 s en reaccionar y mueve su mano para atrapar un objeto que ha caído. (a) ¿Cuán lejos cae el objeto en la Tierra, donde g = 9.8 m/s²? (b) ¿Qué tan lejos cae el objeto sobre la Luna, donde la aceleración debida a la gravedad es 1/6 de la de la Tierra?

107. Un globo de aire caliente se eleva desde el nivel del suelo a una velocidad constante de 3.0 m/s. Un minuto después del despegue, un saco de arena se cae accidentalmente del globo. Calcula (a) el tiempo que le toma al saco de arena llegar al suelo y (b) la velocidad del saco de arena cuando toca el suelo.

108. (a) Se estableció un récord mundial para los hombres de 100 m de carrera en los Juegos Olímpicos de 2008 en Beijing por Usain Bolt de Jamaica. Bolt "cruzó" la línea de meta con un tiempo de 9.69 s. Si suponemos que Bolt aceleró durante 3.00 s para alcanzar su velocidad máxima, y ​​mantuvo esa velocidad para el resto de la carrera, calcula su velocidad máxima y su aceleración. (b) Durante los mismos Juegos Olímpicos, Bolt también estableció el récord mundial en el tablero de 200 m con un tiempo de 19.30 s. Usando las mismas suposiciones que para la carrera de 100 m, ¿cuál fue su velocidad máxima para esta carrera?

109. Un objeto se deja caer desde una altura de 75.0 m sobre el nivel del suelo. (a) Determina la distancia recorrida durante el primer segundo. (b) Determina la velocidad final a la cual el objeto golpea el suelo. (c) Determina la distancia recorrida durante el último segundo de movimiento antes de tocar el suelo.

110. Una bola de acero cae sobre un piso duro desde una altura de 1.50 m y rebota a una altura de 1.45 m. (a) Calcula su velocidad justo antes de que golpee el piso. (b) Calcula su velocidad justo después de que abandona el piso en su camino de regreso. (c) Calcula su aceleración durante el contacto con el piso si ese contacto dura 0.0800 ms (8.00 × 10^-5 s) (d) ¿Cuánto se comprimió la pelota durante su colisión con el piso, asumiendo que el piso es absolutamente rígido?

111. Un objeto es arrojado desde el techo de un edificio de altura h. Durante el último segundo de su descenso, cae una distancia h/3. Calcula la altura del edificio.

Problemas reto

112. En una carrera de 100 m, el ganador tiene un tiempo de 11.2 s. El tiempo del segundo lugar es de 11.6 s. ¿Cuán lejos queda el segundo clasificado detrás del ganador cuando cruza la línea de meta? Supón que la velocidad de cada corredor es constante durante toda la carrera.

113. La posición de una partícula que se mueve a lo largo del eje x varía con el tiempo según x (t) = 5.0t² - 4.0t³ m. Encuentra (a) la velocidad y la aceleración de la partícula como funciones del tiempo, (b) la velocidad y la aceleración en t = 2.0 s, (c) el tiempo en el que la posición es un máximo, (d) el tiempo en el cual la velocidad es cero y (e) la posición máxima.

114. Un ciclista corre al final de una carrera para obtener una victoria. El ciclista tiene una velocidad inicial de 11.5 m/s y acelera a una rata de 0.500 m/s² durante 7.00 s. (a) ¿Cuál es su velocidad final? (b) El ciclista continúa a esta velocidad hasta la línea de meta. Si está a 300 m de la línea de meta cuando comienza a acelerar, ¿cuánto tiempo ahorró? (c) El ganador del segundo lugar estaba a 5.00 m por delante cuando el ganador comenzó a acelerar, pero no pudo acelerar, y corrió a 11.8 m/s hasta la línea de meta. ¿Cuál fue la diferencia en el tiempo de finalización en segundos entre el ganador y el subcampeón? ¿Qué tan atrás estaba el subcampeón cuando el ganador cruzó la línea de llegada?

115. En 1967, el neozelandés Burt Munro estableció el récord mundial de una motocicleta india, en Bonneville Salt Flats en Utah, de 295,38 km/h. El recorrido de ida fue de 8.00 km de largo. Las tasas de aceleración a menudo se describen por el tiempo que lleva alcanzar los 96.0 km/h desde el reposo. Si este tiempo fue de 4,00 s y Burt aceleró a este ritmo hasta que alcanzó su velocidad máxima, ¿cuánto le tomó a Burt completar el recorrido?