Preguntas y problemas - Capítulo II

Preguntas conceptuales

2.2 Escalares y vectores

1. Un pronóstico del tiempo indica que la temperatura se prevé que sea de -5°C al día siguiente. ¿Es esta temperatura un vector o una cantidad escalar? Explique.

2. ¿Cuáles de los siguientes es un vector?: la altura de una persona, la altitud en el monte Everest, la velocidad de una mosca, la edad de la Tierra, el punto de ebullición del agua, el costo de un libro, la población de la Tierra o la aceleración de la gravedad.

3. Da un ejemplo específico de un vector, indicando su magnitud, unidades y dirección.

4. ¿Qué tienen en común los vectores y escalares? ¿Cómo difieren?

5. Supongamos que sumas dos vectores A^→y    B^→. ¿Qué dirección relativa entre ellos produce la resultante con la mayor magnitud? ¿Cuál es la magnitud máxima? ¿Qué dirección relativa entre ellos produce la resultante con la menor magnitud? ¿Cuál es la magnitud mínima?

6. ¿Es posible sumar una cantidad escalar a una cantidad vectorial?

7. ¿Es posible sumar dos vectores de diferentes magnitudes a cero? ¿Es posible sumar tres vectores de diferentes magnitudes a cero? Explique.

8. ¿El odómetro en un automóvil indica una cantidad escalar o vectorial?

9. Cuando un corredor de 10.000 m compite sobre una pista de 400 m cruza la línea de meta, ¿cuál es el desplazamiento neto del corredor? ¿Puede este desplazamiento ser cero? Explique.

10. Un vector tiene una magnitud cero. ¿Es necesario especificar su dirección? Explique.

11. ¿Puede la magnitud de un vector ser negativa?

12. ¿Puede la magnitud del desplazamiento de una partícula ser mayor que la distancia recorrida?

13. Si dos vectores son iguales, ¿qué puedes decir sobre sus componentes? ¿Qué puedes decir sobre sus magnitudes? ¿Qué puedes decir sobre sus direcciones?

14. Si tres vectores suman cero, ¿qué condición geométrica satisfacen?

2.3 Sistemas de coordenadas y componentes de un vector

15. Da un ejemplo de un vector distinto de cero que tiene una componente cero.

16. Explica por qué un vector no puede tener una componente mayor que su propia magnitud.

17. Si dos vectores son iguales, ¿qué puedes decir sobre sus componentes?

18. Si los vectores A^→y   B^→son ortogonales, ¿cuál es la componente de B^→a lo largo de la dirección de A^→? ¿Cuál es la componente de A^→en la dirección de B^→?

19. Si uno de los dos componentes de un vector no es cero, ¿puede la magnitud del otro componente vectorial de este vector ser cero?

20. Si dos vectores tienen la misma magnitud, ¿sus componentes tienen que ser iguales?

2.5 Productos de Vectores

21. ¿Qué pasa con las siguientes expresiones? ¿Cómo puedes corregirlas?
(a) C = A^→B^→, (b) C^→ = A^→b^→, (c)C = A^→×   B^→, (d) C = A ×   B^→, (e) C + 2A^→ = B, (f) C^→ = A×B^→, (g) A^→•   B^→ = A^→×   B^→, (h) A^→= 2A^→•   B^→, (i) C = A^→/B^→, (j) C = A^→/B.

22. Si el producto cruz de dos vectores es nulo, ¿qué puedes decir sobre sus direcciones?

23. Si el producto escalar de dos vectores es nulo, ¿qué puedes decir sobre sus direcciones?

24. ¿Cuál es el producto escalar de un vector con el producto cruz que tiene este vector con otro vector?

Problemas

2.2 Escalares y vectores

25. Un buzo hace un lento descenso a las profundidades del océano. Su posición vertical con respecto a un bote en la superficie cambia varias veces. Hace la primera parada a 9.0 m del barco pero tiene un problema para igualar la presión, por lo que asciende 3.0 m y luego continúa descendiendo por otros 12.0 m hasta la segunda parada. Desde allí, asciende 4 m y luego desciende por 18.0 m, asciende nuevamente por 7 m y desciende nuevamente por 24.0 m, donde hace una parada, esperando a su amigo. Asumiendo la dirección positiva hacia la superficie, exprese su vector resultante de desplazamiento vertical en términos del vector unitario. ¿Cuál es su distancia al bote?

26. En un juego de tira y afloja en un campus, 15 estudiantes tiran de una cuerda en ambos extremos en un esfuerzo por desplazar el nudo central a un lado o al otro. Dos estudiantes tiran con fuerza 196 N a la derecha, cuatro estudiantes tiran con fuerza 98 N a la izquierda, cinco estudiantes tiran con fuerza 62 N a la izquierda, tres estudiantes tiran con fuerza 150 N a la derecha, y un alumno tira con fuerza 250 N hacia la izquierda. Asumiendo la dirección positiva a la derecha, exprese el tirón resultante en el nudo en términos del vector unitario. ¿Qué tan grande es la tracción neta en el nudo? ¿En qué dirección?

27. Supongamos que caminas 18.0 m al oeste y luego 25.0 m al norte. ¿Qué tan lejos estás de tu punto de partida y cuál es la dirección de la brújula de una línea que conecta tu punto de partida con tu posición final? Usa un método gráfico.

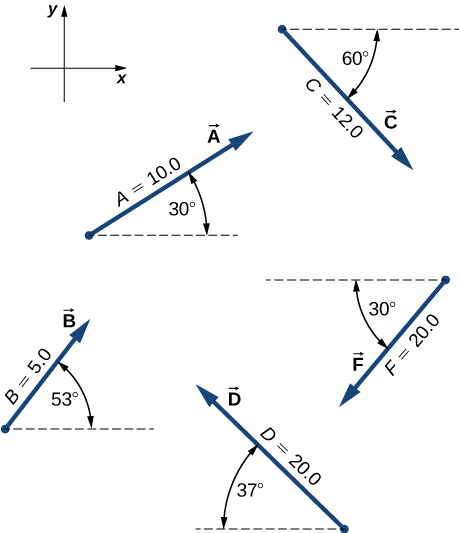
28. Para los vectores dados en la siguiente figura, usa un método gráfico para encontrar los siguientes resultados:
(a) A^→ +   B^→, (b) C^→ +   B^→, (c) C^→ +   F^→, (d)A^→ -   B^→, (e) D^→ -   F^→, (f) A^→ +   2F^→, (g) A^→ -   2D^→ +   2F^→



29. Un repartidor comienza en la oficina de correos, conduce 40 km al norte, luego 20 km al oeste, luego 60 km al noreste, y finalmente 50 km al norte para detenerse a almorzar. Usa un método gráfico para encontrar su vector de desplazamiento resultante.

30. Un perro aventurero se aleja de su casa, corre tres cuadras al este, dos cuadras al norte, una cuadra al este, una cuadra al norte y dos cuadras al oeste. Suponiendo que cada bloque está a unos 100 m, ¿qué tan lejos de casa y en qué dirección está el perro? Usa un método gráfico.

31. En un intento de escapar de una isla desierta, un náufrago construye una balsa y se embarca en el mar. El viento cambia mucho durante el día y sopla en las siguientes direcciones: 2.50 km y 45.0° al noroeste, luego 4.70 km y 60.0° al sureste, luego 1.30 km y 25.0° al suroeste, luego 5,10 km al este, luego 1,70 km y 5,00° al noreste, luego 7,20 km y 55,0° al suroeste, y finalmente 2,80 km y 10,0° al noreste. Usa un método gráfico para encontrar la posición final del náufrago con respecto a la isla.

32. Un pequeño avión vuela 40.0 km en una dirección 60° al noreste y luego vuela 30.0 km en una dirección 15° al noreste. Usa un método gráfico para encontrar la distancia total que cubre el avión desde el punto de partida y la dirección de la ruta hasta la posición final.

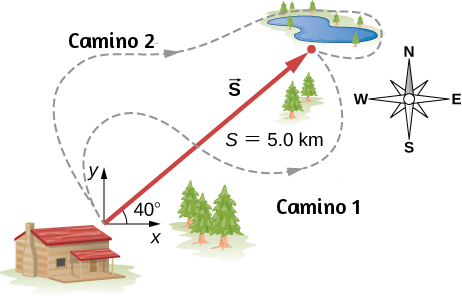
33. Un cazador camina una distancia de 5.0 km en línea recta desde su cabina al lago, como se muestra en la siguiente figura. Usa un método gráfico (la regla del paralelogramo) para determinar el desplazamiento del cazador directamente hacia el este y el desplazamiento directamente hacia el norte que se suma a su vector de desplazamiento resultante. Si el cazador solo caminaba en direcciones este y norte, zigzagueando hacia el lago, ¿cuántos kilómetros tendría que caminar para llegar al lago?



34. Un topógrafo mide la distancia a través de un río que fluye hacia el norte por el siguiente método. Comenzando directamente frente a un árbol en la orilla opuesta, el inspector camina 100 m a lo largo del río para establecer una línea base. Luego mira hacia el árbol y lee que el ángulo desde la línea base hasta el árbol es de 35°. ¿Qué tan ancho es el río?

35. Un peatón camina 6.0 km al este y luego 13.0 km al norte. Usa un método gráfico para encontrar el desplazamiento resultante del peatón y la dirección geográfica.

36. Las magnitudes de dos vectores de desplazamiento son A = 20 m y B = 6 m. ¿Cuáles son los valores más grandes y más pequeños de la magnitud de la resultante R^→= A^→+   B^→?

2.3 Sistemas de coordenadas y componentes de un vector

37. Suponiendo que el eje + x es horizontal y apunta hacia la derecha, resuelve los vectores dados en la siguiente figura en sus componentes escalares y exprésalos en forma de componente vectorial.

38. Supongamos que caminas 18.0 m al oeste y luego 25.0 m al norte. ¿Qué tan lejos estás de tu punto de partida? ¿Cuál es tu vector de desplazamiento? ¿Cuál es la dirección de tu desplazamiento? Supongamos que el eje + x es horizontal a la derecha.

39. Conduce 7.50 km en línea recta en una dirección 15° al noreste. (a) Encuentra las distancias que tendrías que conducir directamente al este y luego al norte para llegar al mismo punto. (b) Demuestra que todavía llegas al mismo punto si las flechas del este y el norte están invertidas. Supongamos que el eje + x está hacia el este.

40. Un trineo es tirado por dos caballos en un terreno plano. La fuerza neta en el trineo se puede expresar en el sistema de coordenadas cartesianas como vector F^→= (- 2980.0i^ + 8200.0j^) N, donde i^ y j^ indican las direcciones a el este y el norte, respectivamente. Encuentra la magnitud y dirección del tirón.

41. Un cazador recorre una distancia de 5.0 km en línea recta desde su cabaña hasta el lago, como se muestra en la siguiente figura. Determina los componentes este y norte de su vector de desplazamiento. ¿Cuántos kilómetros más tendría que caminar si caminara a lo largo de los desplazamientos de los componentes? ¿Cuál es su vector de desplazamiento?



42. Las coordenadas polares de un punto son 4π/3 y 5,50 m. ¿Cuáles son sus coordenadas cartesianas?

43. Dos puntos en un plano tienen coordenadas polares P₁ (2.500 m, π/6) y P₂ (3.800 m, 2π/3). Determina sus coordenadas cartesianas y la distancia entre ellos. Redondea la distancia al centímetro más cercano.

44. Un camaleón está descansando tranquilamente en una pantalla de lanai, esperando que venga un insecto. Asuma el origen de un sistema de coordenadas cartesianas en la esquina inferior izquierda de la pantalla y la dirección horizontal hacia la derecha como la dirección + x. Si sus coordenadas son (2.000 m, 1.000 m), (a) ¿qué tan lejos está de la esquina de la pantalla? (b) ¿Cuál es su ubicación en coordenadas polares?

45. Dos puntos en el plano cartesiano son A (2.00 m, -4.00 m) y B (-3.00 m, 3.00 m). Encuentra la distancia entre ellos y sus coordenadas polares.

46. Una mosca entra por una ventana abierta y se acerca a la habitación. En un sistema de coordenadas cartesianas con tres ejes a lo largo de tres bordes de la habitación, la mosca cambia su posición del punto b (4.0 m, 1.5 m, 2.5 m) al punto e (1.0 m, 4.5 m, 0.5 m). Encuentra los componentes escalares del vector de desplazamiento de la mosca y expresa su vector de desplazamiento en forma de componente vectorial. ¿Cuál es su magnitud?

2.4 Algebra vectorial

47. Para los vectores B^→= -i^ - 4j^ y A^→= -3i^ - 2j^, calcula (a) A^→+ B^→, su magnitud y ángulo de dirección, y (b) A^→- B^→, su magnitud y ángulo de dirección.

48. Una partícula experimenta tres desplazamientos consecutivos dados por los vectores D₁^→= (3.0i^ - 4.0j^ - 2.0k^)mm, D₂^→= (1.0i^ - 7.0j^ + 4.0k^)mm, y D₃^→= (- 7.0i^ + 4.0j^ + 1.0i^) mm. (a) Encuentra el vector de desplazamiento resultante de la partícula. (b) ¿Cuál es la magnitud del desplazamiento resultante? (c) Si todos los desplazamientos fueran a lo largo de una línea, ¿qué distancia viajaría la partícula?

49. Dado dos vectores de desplazamiento A^→= (3.00i^ - 4.00j^ + 4.00k^) m y B^→= (2.00i^ + 3.00j^ - 7.00k^) m, encuentra los desplazamientos y sus magnitudes para (a) C^→= A^→+   B^→y (b) D^→= 2A^→-   B^→.

50. Una avioneta vuela 40.0 km en una dirección 60° al noreste y luego vuela 30.0 km en una dirección 15° al noreste. Utiliza el método analítico para encontrar la distancia total que cubre el plano desde el punto de partida y la dirección geográfica de su vector de desplazamiento. ¿Cuál es su vector de desplazamiento?

51. En un intento de escapar de una isla desierta, un náufrago construye una balsa y se embarca en el mar. El viento cambia mucho durante el día y navega por las siguientes líneas rectas: 2.50 km y 45.0° al noroeste, luego 4.70 km y 60.0° al sureste, luego 1.30 km y 25.0° al suroeste, luego 5,10 km al este, luego a 1,70 km y 5,00° al noreste, luego a 7,20 km y 55,0° al suroeste, y finalmente a 2,80 km y 10,0° al noreste. Usa el método analítico para encontrar el vector resultante de todos sus vectores de desplazamiento. ¿Cuál es su magnitud y dirección?

52. Suponiendo que el eje + x es horizontal a la derecha para los vectores dados en la siguiente figura, use el método analítico para encontrar los siguientes resultados: (a) A^→+   B^→, (b) C^→+   B^→, (c) D^→+   F^→, (d) D^→-   F^→, (e) D^→+   2F^→, (f) A^→+   2F^→, (g) C^→-   2D^→+   3F^→, (h) A^→-   4D^→+   2F^→



53. Dados los vectores en la figura anterior, encuentre el vector R^→que resuelve las ecuaciones (a) D^→+   R^→= F^→ y (b) C^→-   2D^→+   5R^→= 3F^→. Supongamos que el eje + x es horizontal a la derecha.

54. Un repartidor comienza en la oficina de correos, conduce 40 km al norte, luego 20 km al oeste, luego 60 km al noreste, y finalmente 50 km al norte para detenerse a almorzar. Use el método analítico para determinar lo siguiente: (a) Encuentre su vector de desplazamiento neto. (b) ¿Qué tan lejos está el restaurante de la oficina de correos? (c) Si regresa directamente del restaurante a la oficina de correos, ¿cuál es su vector de desplazamiento en el viaje de regreso? (d) ¿Cuál es el rumbo de su brújula en el viaje de regreso? Supongamos que el eje + x está hacia el este.

55. Un perro aventurero se aleja de su casa, corre tres cuadras al este, dos cuadras al norte, y una cuadra al este, una cuadra al norte, y dos cuadras al oeste. Suponiendo que cada bloque tiene aproximadamente 100 yardas, usa el método analítico para encontrar el vector de desplazamiento neto del perro, su magnitud y su dirección. Supongamos que el eje + x está hacia el este. ¿Cómo se vería afectada tu respuesta si cada bloque fuera de aproximadamente 100 m?

56. Si D^→= (6.00i^ - 8.00j^) m, B^→= (- 8.00i^ + 3.00j^) m, y A^→= (26.0i^ + 19.0j^) m, encuentra las constantes desconocidas a y b tales que aD^→+ bB^→+ A^→= 0.

57. Dado el vector de desplazamiento D^→= (3i^ - 4j^) m, encuentra el vector de desplazamiento R^→de modo que D^→+   R^→= -4Dj^

58. Encuentra el vector unitario de dirección para las siguientes cantidades de vectores: (a) Fuerza F^→= (3.0i^ - 2.0j^) N, (b) desplazamiento D^→= (- 3.0i^ - 4.0j^ ) m, y (c) velocidad v^→= (- 5.00i^ + 4.00j^) m/s.

59. En un punto en el espacio, la dirección del vector de campo eléctrico se da en el sistema cartesiano por el vector unitario E^ = 1/5√i^ - 2/5√j^. Si la magnitud del vector de campo eléctrico es E = 400.0 V/m, ¿cuáles son los componentes escalares E_x, E_y y E_z del vector de campo eléctrico E^→en este punto? ¿Cuál es el ángulo de dirección θ_E del vector del campo eléctrico en este punto?

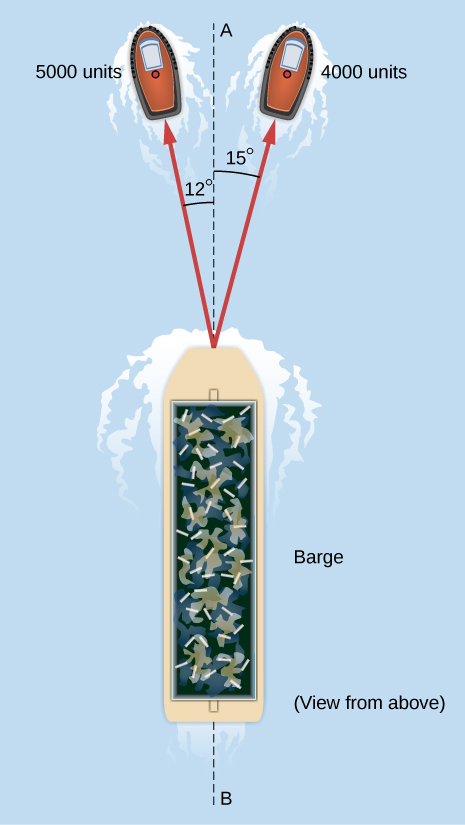
60. Una barcaza es tirada por los dos remolcadores que se muestran en la siguiente figura. Un remolcador tira de la barcaza con una fuerza de magnitud 4000 unidades de fuerza a 15° por encima de la línea AB (observa la figura) y el otro remolcador tira de la barcaza con una fuerza de 5000 unidades de fuerza a 12° debajo de la línea AB. Halla las fuerzas de tracción de sus componentes escalares y encuentra los componentes de la fuerza resultante sobre de la barcaza. ¿Cuál es la magnitud de la tracción resultante? ¿Cuál es su dirección relativa a la línea AB?



61. En la torre de control de un aeropuerto regional, un controlador de tránsito aéreo monitorea dos aeronaves a medida que cambian sus posiciones con respecto a la torre de control. Un avión es un portaaviones Boeing 747 y el otro es Douglas DC-3. El Boeing se encuentra a una altitud de 2500 m, ascendiendo a 10° sobre la horizontal, y moviéndose 30° al noroeste. El DC-3 se encuentra a una altitud de 3000 m, subiendo a 5° por encima de la horizontal y navegando directamente hacia el oeste. (a) Encuentra los vectores de posición de los planos relativos a la torre de control. (b) ¿Cuál es la distancia entre los aviones en el momento en que el controlador de tránsito aéreo anota sus posiciones?

62. Suponiendo que el eje + x es horizontal a la derecha para los vectores en la figura siguiente, busque los siguientes productos escalares: (a) A^→•   C^→, (b) A^→•   F^→, (c) D^→•   C^→, (d) A^→•   (F^→+   2C^→), (e) i^•  F^→, (f) j^•  B^→, (g) (3i^ - j^)•  B^→, (h) B^•B^



63. Suponiendo que el eje + x es horizontal a la derecha para los vectores en la figura anterior, encuentre (a) el componente del vector A^→a lo largo del vector C^→, (b) el componente del vector C^→a lo largo del vector A^→, (c) el componente del vector i^ a lo largo del vector F^→, y (d) el componente del vector F^→a lo largo del vector i^.

64. Encuentra el ángulo entre los vectores para (a) D^→= (−3.0i^ − 4.0j^)m y A^→ = (−3.0i^ + 4.0j^)m, (b) D^→= (2.0i^ − 4.0j^ + k^)m y B^→= (−2.0i^ + 3.0j^ + 2.0k^)m.

65. Encuentra los ángulos que el vector D^→= (2.0i^ - 4.0j^ + k^) m hace con los ejes x, y y z.

66. Demuestra que el vector de fuerza D^→= (2.0i^ - 4.0j^ + k^) N es ortogonal al vector de fuerza G^→= (3.0i^ + 4.0j^ + 10.0k^) N.

67. Suponiendo que el eje + x es horizontal a la derecha para los vectores en la figura anterior, encuentre los siguientes productos vectoriales: (a) A^→×   C^→, (b) A^→×   F^→, (c) D^→×   C^→, (d) A^→×   (F^→+   2C)^→, (e) i^ ×   B^→, (f) j^ ×   B^→, (g) (3i^ - j^) ×   B^→, (h) B^ × B^.

68. Encuentra el producto cruz A^→×   C^→para: (a) A^→= (2i^ - 4j^ + k^) y C^→= (3i^ + 4j^ + 10k^), (b) A^→= (3i^ + 4j^ + 10k^) y C^→= (2i^ - 4j^ + k^), (c) C^→= (-2i^ + 3j^ + 2k^) y A^→= -9j^

69. Para los vectores en la figura anterior, encuentra: (a) (A^→×   F)^→•  D^→, (b) (A^→×   F)^→•  (D^→×   B)^→, (c) (A^→×   F)^→•  (D^→×   B)^→

70. (a) Si (A^→×   F)^→= (B^→×   F)^→, podemos concluir A^→ = B^→, (b) si FA^→BF^→podemos concluir A^→ = B^→, ¿por qué sí?, por qué no?

Problemas adicionales

71. Vuelas 32.0 km en línea recta, en aire quieto, en la dirección 35.0° suroeste. (a) Encuentra las distancias que deberías volar hacia el sur y luego hacia el oeste para llegar al mismo punto. (b) Encuentra las distancias que tendrías que volar primero en una dirección de 45.0° al suroeste y luego en una dirección de 45.0° al noroeste . Ten en cuenta que éstos son los componentes del desplazamiento a lo largo de un conjunto diferente de ejes, es decir, el que gira 45° con respecto a los ejes en (a).

72. Las coordenadas rectangulares de un punto vienen dadas por (2, y) y sus coordenadas polares están dadas por (r, π/6) (r, π/6). Encuentra y y r.

73. Si las coordenadas polares de un punto son (r, φ) y sus coordenadas rectangulares son (x, y), determina las coordenadas polares de los siguientes puntos: (a) (-x, y), (b) (-2x, -2y) y (c) (3x, -3y).

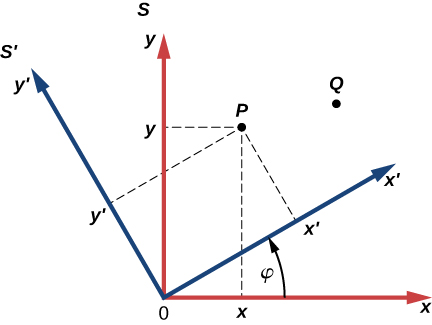
74. Los vectores A^→ y B^→ tienen magnitudes idénticas de 5.0 unidades. Encuentra el ángulo entre ellos si A^→ + B^→= 5√2j^.

75. Comenzando en la isla de Moi en un archipiélago desconocido, un barco de pesca hace un viaje redondo con dos paradas en las islas de Noi y Poi. Navega desde Moi por 4.76 millas náuticas (nmi) en una dirección 37° al noreste de Noi. Desde Noi, navega 69° al noroeste hasta Poi. En su etapa de regreso de Poi, navega 28° al sureste. ¿A qué distancia navega el barco entre Noi y Poi? ¿Qué distancia navega entre Moi y Poi? Expresa tu respuesta en millas náuticas y en kilómetros. Nota: 1 nmi = 1852 m.

76. Un controlador de tráfico aéreo nota dos señales de dos aviones en el monitor del radar. Un avión está a una altitud de 800 m y en una distancia horizontal de 19.2 km a la torre, en una dirección de 25° suroeste. El segundo avión está a una altura de 1100 m y su distancia horizontal es de 17.6 km y 20° suroeste. ¿Cuál es la distancia entre estos aviones?

77. Demuestre que cuando A^→+   B^→= C^→, entonces C² = A² + B² + 2ABcosφ, donde φ es el ángulo entre los vectores AA^→y B^→.

78. Cuatro vectores de fuerza tienen la misma magnitud f. ¿Cuál es la magnitud más grande que puede tener el vector de fuerza resultante cuando se agregan estas fuerzas? ¿Cuál es la menor magnitud de la resultante? Haz un gráfico de ambas situaciones.

79. Un patinador se desliza a lo largo de una trayectoria circular de radio 5,00 m en el sentido de las agujas del reloj. Cuando patina alrededor de la mitad del círculo, comenzando desde el punto oeste, encuentra (a) la magnitud de su vector de desplazamiento y (b) la distancia que patinó realmente. (c) ¿Cuál es la magnitud de su vector de desplazamiento cuando patina alrededor del círculo y regresa al punto oeste?

80. Un perro obstinado está siendo sostenido con una correa por su dueño. En un momento, el perro encuentra un olor interesante en algún lugar en el suelo y quiere explorarlo en detalle, pero el dueño se impacienta y tira de la correa con fuerza F^→= (98.0i + 132.0j + 32.0k) NF → = (98.0i^ + 132.0j^ + 32.0k^) N a lo largo de la correa. (a) ¿Cuál es la magnitud de la fuerza de tracción? (b) ¿Qué ángulo hace la correa con la vertical?

81. Si el vector de velocidad de un oso polar es u^→= (- 18.0i^ - 13.0j^) km/h, ¿qué tan rápido y en qué dirección geográfica se dirige? Aquí, i^ y j^ son direcciones hacia el este y el norte geográficos, respectivamente.

82. Encuentra los componentes escalares de los vectores tridimensionales G^→y H^→en la siguiente figura y escribe el vector usando los vectores unitarios.

    

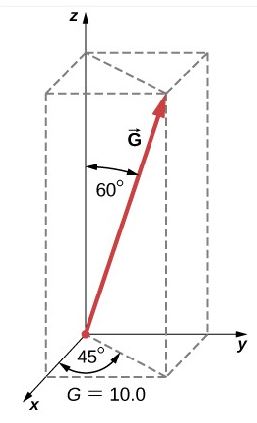
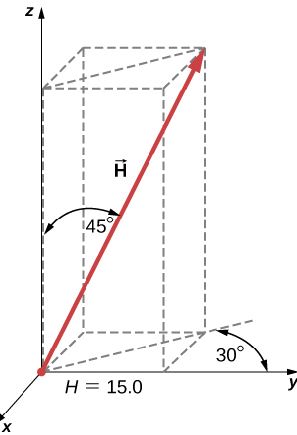
83. Un buzo explora un arrecife poco profundo frente a la costa de Belice. Inicialmente nada 90.0 m al norte, gira hacia el este y continúa durante 200.0 m, luego sigue un gran mero durante 80.0 m en la dirección 30° al noreste. Mientras tanto, una corriente local lo desplaza 150.0 m al sur. Suponiendo que la corriente ya no está presente, ¿en qué dirección y hasta dónde debería nadar ahora para volver al punto donde comenzó?

84. Un vector de fuerza A^→tiene componentes x e y, respectivamente, de -8.80 unidades de fuerza y 15.00 unidades de fuerza. Los componentes x e y del vector de fuerza B^→son, respectivamente, 13.20 unidades de fuerza y -6.60 unidades de fuerza. Encuentra las componentes del vector de fuerza C^→que satisfaga la ecuación vectorial A^→- B^→+ 3C^→= 0.

85. Los vectores A^→y B^→son dos vectores ortogonales en el plano xy, y tienen magnitudes idénticas. Si A^→= 3.0i^ + 4.0j^, encuentre B^→.

86. Para los vectores tridimensionales en la siguiente figura, encuentre (a) G^→×   H^→, (b) |G^→×   H|^→, y (c) G^→•   H^→.

    

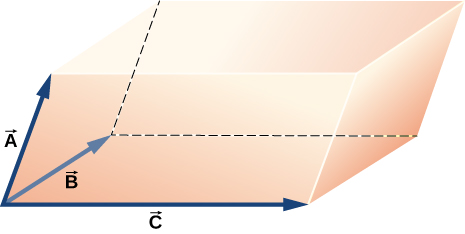
87. Demuestra que (B^→×   C)^→•   A^→ es el volumen del paralelepípedo, con los bordes formados por los tres vectores en la siguiente figura.

Problemas reto

88. El vector B^→es de 5.0 cm de largo y el vector A^→tiene 4.0 cm de largo. Encuentra el ángulo entre estos dos vectores cuando |A^→+ B|^→ = 3.0cm y |A^→- B|^→ = 3.0cm.

89. ¿Cuál es el componente del vector de fuerza G^→= (3.0i^ + 4.0j^ + 10.0k^) N a lo largo del vector de fuerza H^→ = (1.0i^ + 4.0j^) N?

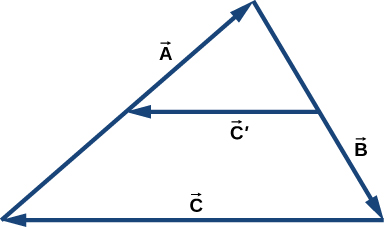
90. La siguiente figura muestra un triángulo formado por los tres vectores A^→, B^→ y C^→. Si el vector C^→ se dibuja entre los puntos medios de los vectores A^→y B^→, muestra que C^→ = C/2^→.



91. Las distancias entre puntos en un plano no cambian cuando se rota un sistema de coordenadas. En otras palabras, la magnitud de un vector es invariante bajo rotaciones del sistema de coordenadas. Supongamos que un sistema de coordenadas S gira sobre su origen en un ángulo φ para convertirse en un nuevo sistema de coordenadas S', como se muestra en la siguiente figura. Un punto en un plano tiene coordenadas (x, y) en S y coordenadas (x', y') en S'. (a) Demuestra que, durante la transformación de la rotación, las coordenadas en S'se expresan en términos de las coordenadas en S por las siguientes relaciones:

          x′ = xcosφ + ysenφ
          y′ = -xsenφ + ycosφ

(b) Muestra que la distancia del punto P al origen es invariante bajo rotaciones del sistema de coordenadas. Aquí, debes mostrar que

          √x² + y^{2━━━━}= √x'² + y'^{2━━━━}

(c) Muestra que la distancia entre los puntos P y Q es invariante bajo rotaciones del sistema de coordenadas. Aquí, debes mostrar que

          √(x_P - x_Q)² + (y_P - y_Q)^{2━━━━━━━━━━━}= √(x'_P - x'_Q)² + (y'_P - y'_Q)^{2━━━━━━━━━━━━}