Preguntas y problemas - Capítulo X

Preguntas conceptuales

10.2 Ley de gravitación universal de Newton

1. La acción a distancia, como es el caso de la gravedad, se pensó una vez que era ilógica y, por lo tanto, falsa. ¿Cuál es el último determinante de la verdad en la ciencia, y por qué fue esta acción a una distancia finalmente aceptada?

2. En la ley de la gravitación universal, Newton asumió que la fuerza era proporcional al producto de las dos masas (~ m₁m₂). Si bien todas las conjeturas científicas deben ser verificadas experimentalmente, ¿puedes proporcionar argumentos sobre por qué debe ser así? (Es posible que desees considerar ejemplos simples en los que cualquier otra forma daría lugar a resultados contradictorios).

10.3 Gravitación cerca de la superficie de la Tierra

3. ¿Los ingenieros deben tener en cuenta la rotación de la Tierra al construir edificios muy altos en cualquier lugar que no sea el ecuador o muy cerca de los polos?

10.4 Energía potencial gravitacional y energía total

4. Se afirmó que un satélite con energía total negativa está en una órbita confinada, mientras que uno con cero o energía total positiva está en una órbita sin límites. ¿Por qué es esto cierto? ¿Qué opción para la energía potencial gravitatoria se hizo de tal manera que esto sea cierto?

5. Se demostró que la energía requerida para elevar un satélite a una órbita terrestre baja (el cambio en la energía potencial) es solo una pequeña fracción de la energía cinética necesaria para mantenerla en órbita. ¿Es esto cierto para órbitas más grandes? ¿Hay una tendencia a la relación de energía cinética a cambiar en energía potencial a medida que aumenta el tamaño de la órbita?

10.5 Órbitas satelitales y energía

6. Un estudiante argumenta que un satélite en órbita está en caída libre porque el satélite sigue cayendo hacia la Tierra. Otro dice que un satélite en órbita no está en caída libre porque la aceleración debida a la gravedad no es de 9.80 m/s². ¿Con quién estás de acuerdo y por qué?

7. Muchos satélites se colocan en órbitas geosincrónicas. ¿Qué tiene de especial estas órbitas? Para una red de comunicación global, ¿cuántos de estos satélites se necesitarían?

10.6 Las leyes de movimiento planetario de Kepler

8. ¿Las leyes de Kepler son puramente descriptivas o contienen información causal?

9. En el siguiente diagrama para un satélite en una órbita elíptica sobre una masa mucho más grande, indica dónde está su velocidad máxima y dónde está la menor. ¿Qué ley de conservación dicta este comportamiento? Indica las direcciones de la fuerza, aceleración y velocidad en estos puntos. Dibuja vectores para estas mismas tres cantidades en los dos puntos donde se cruza el eje y (a lo largo del eje semi-menor) y a partir de esto determina si la velocidad aumenta o disminuye a un máximo o a un mínimo.

10.7 Fuerzas de marea

10. Cuando un objeto cae en un agujero negro, aumentan las fuerzas de marea. ¿Estas fuerzas de marea siempre destrozarán el objeto mientras se acerca al radio de Schwarzschild? ¿De qué manera la masa del agujero negro y el tamaño del objeto afectan tu respuesta?

10.8 La teoría de la gravedad de Einstein

11. El principio de equivalencia establece que todos los experimentos realizados en un laboratorio en un campo gravitatorio uniforme no se pueden distinguir de los realizados en un laboratorio que no se encuentra en un campo gravitatorio, sino que se acelera de manera uniforme. Para el último caso, considera lo que le ocurre a un rayo láser de cierta altura disparado perfectamente horizontalmente al piso, a través del laboratorio en aceleración (Mira esto desde un marco no acelerado fuera del laboratorio). En relación con la altura del láser, ¿dónde golpeará el rayo láser la pared más alejada? ¿Qué dice esto sobre el efecto de un campo gravitatorio en la luz? ¿El hecho de que la luz no tenga masa hace una diferencia en el argumento?

12. Cuando una persona se acerca al radio de Schwarzschild de un agujero negro, los observadores externos ven que todos los procesos de esa persona (sus relojes, su ritmo cardíaco, etc.) se ralentizan y se detienen cuando alcanzan el radio de Schwarzschild (La persona que cae en el agujero negro ve sus propios procesos no afectados). Pero la velocidad de la luz es la misma en todas partes para todos los observadores. ¿Qué dice esto sobre el espacio cuando te acercas al agujero negro?

Problemas

10.2 Ley de gravitación universal de Newton

13. Evalúa la magnitud de la fuerza gravitatoria entre dos bolas esféricas de acero de 5 kg separadas por una distancia de centro a centro de 15 cm.

14. Estima la fuerza gravitacional entre dos luchadores de sumo, con masas de 220 kg y 240 kg, cuando están abrazados y sus centros están a 1,2 m de distancia.

15. La astrología prepara gran parte de la posición de los planetas en el momento del nacimiento. La única fuerza conocida que un planeta ejerce en la Tierra es gravitatoria. (a) Calcula la fuerza gravitacional ejercida sobre un bebé de 4.20 kg por un padre de 100 kg a 0.200 m de distancia al nacer (él está ayudando, por lo que está cerca del niño). (b) Calcula la fuerza sobre el bebé debido a Júpiter si está a su distancia más cercana a la Tierra, a unos 6,29 × 10¹¹ m de distancia. ¿Cómo se compara la fuerza de Júpiter con el bebé con la fuerza del padre sobre el bebé? Otros objetos en la habitación y el edificio del hospital también ejercen fuerzas gravitacionales similares (Por supuesto, podría haber una fuerza desconocida actuando, pero los científicos primero necesitan estar convencidos de que incluso hay un efecto, y mucho menos que una fuerza desconocida lo cause).

16. Una montaña a 10.0 km de una persona ejerce una fuerza gravitacional sobre él igual al 2.00% de su peso. (a) Calcula la masa de la montaña. (b) Compara la masa de la montaña con la de la Tierra. (c) ¿Qué es irracional sobre estos resultados? (d) ¿Qué premisas son irrazonables o inconsistentes? (Ten en cuenta que las mediciones gravitacionales precisas pueden detectar fácilmente el efecto de las montañas cercanas y las variaciones en la geología local)

17. La Estación Espacial Internacional tiene una masa de aproximadamente 370,000 kg. (a) ¿Cuál es la fuerza sobre un astronauta de 150 kg si está a 20 m del centro de masa de la estación? (b) ¿Cuán precisa crees que sería tu respuesta?



18. El asteroide Toutatis pasó cerca de la Tierra en 2006 a cuatro veces la distancia a nuestra Luna. Esta fue la aproximación más cercano que tendremos hasta el 2060. Si tiene una masa de 5.0 × 10¹³ kg, ¿qué fuerza ejerció sobre la Tierra en su punto más cercano?

19. (a) ¿Cuál fue la aceleración de la Tierra causada por el asteroide Toutatis (ver problema anterior) en su punto más cercano? (b) ¿Cuál fue la aceleración de Toutatis en este punto?

10.3 Gravitación cerca de la superficie de la Tierra

20. (a) Calcula la masa de la Tierra dada la aceleración debida a la gravedad en el Polo Norte que se mide en 9.832 m/s² y el radio de la Tierra en el polo es de 6356 km. (b) Compara esto con el valor de los datos de la NASA de la Tierra de 5.9726 × 10²⁴kg.

21. (a) ¿Cuál es la aceleración debida a la gravedad en la superficie de la Luna? (b) ¿En la superficie de Marte? La masa de Marte es 6.418 × 10²³ kg y su radio es 3.38 × 10⁶ m.

22. a) Calcula la aceleración debida a la gravedad en la superficie del sol. (b) ¿Por qué factor aumentaría tu peso si pudieras pararte sobre el sol? (No importa que no puedas)

23. La masa de una partícula es 15 kg. (a) ¿Cuál es su peso en la Tierra? (b) ¿Cuál es su peso en la Luna? (c) ¿Cuál es su masa en la Luna? (d) ¿Cuál es su peso en el espacio exterior lejos de cualquier cuerpo celeste? (e) ¿Cuál es su masa en este punto?

24. En un planeta cuyo radio es de 1.2 × 10⁷ m, la aceleración debida a la gravedad es de 18 m/s². Cuál es la masa del planeta?

25. El diámetro medio del planeta Saturno es 1.2 × 10⁸ m, y su densidad de masa media es 0.69 g/cm³. Encuentra la aceleración debida a la gravedad en la superficie de Saturno.

26. El diámetro medio del planeta Mercurio es de 4,88 × 10⁶ m, y la aceleración debida a la gravedad en su superficie es de 3,78 m/s². Estima la masa de este planeta.

27. La aceleración debida a la gravedad en la superficie de un planeta es tres veces mayor que en la superficie de la Tierra. Se sabe que la densidad de masa del planeta es el doble que la de la Tierra. ¿Cuál es el radio de este planeta en términos del radio de la Tierra?

28. Un cuerpo en la superficie de un planeta con el mismo radio que la Tierra pesa 10 veces más que en la Tierra. ¿Cuál es la masa de este planeta en términos de la masa de la Tierra?

10.4 Energía potencial gravitacional y energía total

29. Encuentra la velocidad de escape de un proyectil desde la superficie de Marte.

30. Encuentra la velocidad de escape de un proyectil desde la superficie de Júpiter.

31. ¿Cuál es la velocidad de escape de un satélite ubicado en la órbita de la Luna sobre la Tierra? Supongamos que la Luna no está cerca.

32. (a) Evalúa la energía potencial gravitatoria entre dos bolas esféricas de acero de 5.00 kg separadas por una distancia de centro a centro de 15.0 cm. (b) Suponiendo que ambas están inicialmente en reposo una respecto de la otra en el espacio profundo, utiliza la conservación de la energía para determinar qué tan rápido viajarán en el momento del impacto. Cada esfera tiene un radio de 5.10 cm.

33. Se detecta un asteroide de tamaño promedio ubicado a 5.0 × 10⁷ km de la Tierra con una masa de 2.0 × 10¹³ kg, que se dirige directamente hacia la Tierra con una velocidad de 2.0 km/s. ¿Cuál será su velocidad justo antes de que llegue a nuestra atmósfera? (Puedes ignorar el tamaño del asteroide).

34. (a) ¿Cuál será la energía cinética del asteroide en el problema anterior justo antes de que llegue a la Tierra? b) Compara esta energía con la salida de la bomba de fisión más grande, 2100 TJ. ¿Qué impacto tendría esto en la Tierra?

35. (a) ¿Cuál es el cambio en la energía de una carga útil de 1000 kg tomada desde el reposo en la superficie de la Tierra y colocada en reposo en la superficie de la Luna? (b) ¿Cuál sería la respuesta si la carga útil se toma desde la superficie de la Luna a la Tierra? ¿Es este un cálculo razonable de la energía necesaria para mover una carga útil hacia adelante y hacia atrás?

10.5 Órbitas satelitales y energía

36. Si un planeta con 1,5 veces la masa de la Tierra viajara en la órbita de la Tierra, ¿cuál sería su período?

37. Dos planetas en órbitas circulares alrededor de una estrella tienen velocidades de v y 2v. (a) ¿Cuál es la relación de los radios orbitales de los planetas? (b) ¿Cuál es la proporción de sus períodos?

38. Usando la distancia promedio de la Tierra al Sol, y el período orbital de la Tierra, (a) encuentra la aceleración centrípeta de la Tierra en su movimiento sobre el Sol. (b) Compara este valor con el de la aceleración centrípeta en el ecuador debido a la rotación de la Tierra.

39. ¿Cuál es el radio orbital de un satélite de la Tierra que tiene un período de 1,00 h? (b) ¿Qué es irracional sobre este resultado?

40. Calcula la masa del Sol en base a los datos de la órbita de la Tierra y compara el valor obtenido con la masa real del Sol.

41. Encuentra la masa de Júpiter basándote en el hecho de que Io, su luna más interna, tiene un radio orbital promedio de 421,700 km y un período de 1,77 días.

42. Las observaciones astronómicas de nuestra galaxia de la Vía Láctea indican que tiene una masa de aproximadamente 8.0 × 10¹¹ masas solares. Una estrella que orbita en la periferia de la galaxia está a unos 6,0 × 10⁴ años luz de su centro. (a) ¿Cuál debería ser el período orbital de esa estrella? (b) Si su período es de 6.0 × 10⁷ años, ¿cuál es la masa de la galaxia? Tales cálculos se usan para implicar la existencia de otra materia, como un agujero negro muy masivo en el centro de la Vía Láctea.

43. (a) Para evitar que un satélite pequeño se desplace hacia un asteroide cercano, se coloca en órbita con un período de 3,02 horas y un radio de 2,0 km. ¿Cuál es la masa del asteroide? (b) ¿Esta masa parece razonable para el tamaño de la órbita?

44. La Luna y la Tierra giran alrededor de su centro de masa común, que se encuentra a unos 4700 km del centro de la Tierra (Esto es 1690 km debajo de la superficie). (a) Calcula la aceleración debido a la gravedad de la Luna en ese punto. (b) Calcula la aceleración centrípeta del centro de la Tierra al girar alrededor de ese punto una vez cada mes lunar (aproximadamente 27.3 d) y compáralo con la aceleración que se encuentra en la parte (a). Comenta si son iguales o no y por qué deberían o no deberían serlo.

45. El Sol orbita alrededor de la Vía Láctea una vez cada 2.60 × 10⁸ años, con una órbita más o menos circular que promedia un radio de 3.00 × 10⁴ años luz (Un año luz es la distancia recorrida por la luz en 1 año). Calcula la aceleración centrípeta del Sol en su órbita galáctica. ¿Tu resultado respalda la afirmación de que un marco de referencia casi inercial puede ubicarse en el Sol? (b) Calcula la velocidad promedio del Sol en su órbita galáctica. ¿Te sorprende la respuesta?

46. ​​Un satélite de la Tierra geosincrónico es aquel que tiene un período orbital de, precisamente, 1 día. Tales órbitas son útiles para la comunicación y la observación del clima porque el satélite permanece sobre el mismo punto en la Tierra (siempre que orbite en el plano ecuatorial en la misma dirección que la rotación de la Tierra). Calcula el radio de dicha órbita.

10.6 Las leyes de movimiento planetario de Kepler

47. Calcula la masa del Sol en base a los datos de la órbita media de la Tierra y comparae el valor obtenido con el valor comúnmente listado por el Sol de 1.989 × 10³⁰kg.

48. Io orbita alrededor de Júpiter con un radio promedio de 421.700 km y un período de 1.769 días. En base a estos datos, ¿cuál es la masa de Júpiter?

49. El radio orbital "medio" enumerado para los objetos astronómicos que orbitan alrededor del Sol normalmente no es un promedio integrado, pero se calcula de manera que da el período correcto cuando se aplica a la ecuación para órbitas circulares. ¿Cuál es el radio orbital promedio en términos de afelio y perihelio?

50. El perihelio del cometa de Halley es de 0.586 UA y el afelio de 17.8 UA. Dado que su velocidad en el perihelio es de 55 km/s, ¿cuál es la velocidad en el afelio (1UA = 1.496 × 10¹¹ m)? (Sugerencia: puedes usar la conservación de la energía o el momento angular, pero este último es mucho más fácil).

51. El perihelio del cometa Lagerkvist es de 2.61 UA y tiene un período de 7.36 años. Demuestra que el afelio para este cometa es 4.95 AU.

52. ¿Cuál es la relación entre la velocidad en el perihelio y la del afelio para el cometa Lagerkvist en el problema anterior?

53. Eros tiene una órbita elíptica alrededor del Sol, con una distancia del perihelio de 1.13 UA y una distancia de 1.78 UF afelio. ¿Cuál es el período de su órbita?

10.7 Fuerzas de marea

54. (a) ¿Cuál es la diferencia entre las fuerzas en una masa de 1.0 kg en el lado cercano de Io y el lado distante debido a Júpiter? Io tiene un radio medio de 1821 km y un radio orbital promedio sobre Júpiter de 421,700 km. (b) Compara esta diferencia con la calculada para la diferencia en la Tierra debido a la Luna calculada en el Ejemplo 10.14. Las fuerzas de marea son la causa de la actividad volcánica de Io.

55. Si el Sol se colapsase en un agujero negro, el punto de no retorno para un investigador sería de aproximadamente 3 km desde la singularidad central. ¿Podría el investigador sobrevivir incluso a 300 km del centro? Responde esto al encontrar la diferencia en la atracción gravitatoria que ejercen los agujeros negros en una masa de 1.0 kg en la cabeza y en los pies del investigador.

56. Considera la figura 10.23 en Fuerzas de marea. Este diagrama representa las fuerzas de marea para las mareas vivas. Dibuja un diagrama similar para las mareas muertas. (Sugerencia: para simplificar, imagina que el Sol y la Luna contribuyen por igual. Su diagrama sería la suma vectorial de dos campos de fuerza (como en la figura 10.23), reducido en un factor de dos y superpuesto en ángulos rectos).

10.8 La teoría de la gravedad de Einstein

57. ¿Cuál es el radio de Schwarzschild para el agujero negro en el centro de nuestra galaxia si tiene una masa de 4 millones de masas solares?

58. ¿Cuál sería el radio de Schwarzschild, en años luz, si nuestra galaxia de la Vía Láctea de 100 mil millones de estrellas colapsó en un agujero negro? Compara ésto con nuestra distancia desde el centro, alrededor de 13,000 años luz.

Problemas adicionales

59. Una estrella de neutrones es una estrella fría y colapsada con densidad nuclear. Una estrella de neutrones particular tiene una masa dos veces mayor a la de nuestro Sol con un radio de 12.0 km. (a) ¿Cuál sería el peso de un astronauta de 100 kg parado en su superficie? (b) ¿Qué nos dice esto sobre aterrizar en una estrella de neutrones?

60. (a) ¿Qué tan lejos del centro de la Tierra la fuerza gravitacional neta de la Tierra y la Luna sobre un objeto sería cero? (b) Establecer las magnitudes de las fuerzas iguales debería dar como resultado dos respuestas de la cuadrática. ¿Entiendes por qué hay dos posiciones, pero solo una donde la fuerza neta es cero?

61. ¿Qué tan lejos del centro del Sol la fuerza gravitacional neta de la Tierra y el Sol en una nave espacial sería cero?

62. Calcula los valores de g en la superficie de la Tierra para los siguientes cambios en las propiedades de la Tierra: (a) su masa se duplica y su radio se reduce a la mitad; (b) su densidad de masa se duplica y su radio no cambia; (c) su densidad de masa se reduce a la mitad y su masa no cambia.

63. Supongamos que puedes comunicarte con los habitantes de un planeta en otro sistema solar. Te dicen que en su planeta, cuyo diámetro y masa son 5,0 × 10³ km y 3,6 × 10²³ kg, respectivamente, el registro para el salto de altura es de 2,0 m. Dado que este registro está cerca de 2,4 m en la Tierra, ¿qué concluirías sobre la capacidad de salto de tus amigos extraterrestres?

64. (a) Supón que tu peso medido en el ecuador es la mitad de tu peso medido en el polo de un planeta cuya masa y diámetro son iguales a los de la Tierra. ¿Cuál es el período de rotación del planeta? (b) ¿Necesitarías tomar en cuenta la forma de este planeta?

65. Se pesa un cuerpo de 100 kg de masa en el Polo Norte y en el ecuador con una balanza de resorte. ¿Cuál es la lectura de la escala en estos dos puntos? Supongamos que g = 9.83 m/s² en el polo.

66. Encuentra la velocidad necesaria para escapar del sistema solar comenzando desde la superficie de la Tierra. Supongamos que no hay otros cuerpos involucrados y no tienen en cuenta el hecho de que la Tierra se está moviendo en su órbita. (Sugerencia: la ecuación 10.6 no se aplica. Usa la Ecuación 10.5 e incluye la energía potencial de la Tierra y del Sol).

67. Considera el problema anterior e incluye el hecho de que la Tierra tiene una velocidad orbital alrededor del Sol de 29.8 km/s. (a) ¿Qué velocidad relativa a la Tierra se necesitaría y en qué dirección debería abandonar la Tierra? (b) ¿Cuál será la forma de la trayectoria?

68. Se observa un cometa a 1.50 AU del Sol con una velocidad de 24.3 km/s. ¿Este cometa está en una órbita ligada o no ligada?

69. Un asteroide tiene una velocidad de 15.5 km/s cuando está ubicado a 2.00 UA del sol. En su punto más cercano, está a 0.400 UA del Sol. ¿Cuál es su velocidad en ese punto?

70. Los desechos espaciales de los satélites antiguos y sus lanzadores se están convirtiendo en un peligro para otros satélites. (a) Calcula la velocidad de un satélite en una órbita de 900 km sobre la superficie de la Tierra. (b) Supongamos que un remache flojo se encuentra en una órbita del mismo radio que intersecta la órbita del satélite en un ángulo de 90°. ¿Cuál es la velocidad del remache con respecto al satélite justo antes de golpearlo? (c) Si su masa es 0.500 g, y se detiene en el interior del satélite, ¿cuánta energía en julios genera la colisión? (Supongamos que la velocidad del satélite no cambia apreciablemente, porque su masa es mucho mayor que la del remache).

71. Un satélite de 1000 kg de masa está en órbita circular alrededor de la Tierra. El radio de la órbita del satélite es igual a dos veces el radio de la Tierra. (a) ¿Qué tan lejos está el satélite? (b) Encuentra las energías cinéticas, potenciales y totales del satélite.

72. Después de que Ceres fuera promovido a planeta enano, ahora reconocemos que el asteroide conocido más grande es Vesta, con una masa de 2,67 × 10²⁰ kg y un diámetro que varía entre 578 km y 458 km. Suponiendo que Vesta es esférica con un radio de 520 km, encuentre la velocidad de escape aproximada desde su superficie.

73. (a) Usando los datos en el problema anterior para el asteroide Vesta, ¿cuál sería el período orbital para una sonda espacial en una órbita circular de 10.0 km desde su superficie? (b) ¿Por qué este cálculo es marginalmente útil en el mejor de los casos?

74. ¿Cuál es la velocidad orbital de nuestro sistema solar sobre el centro de la Vía Láctea? Supongamos que la masa dentro de una esfera de radio igual a nuestra distancia del centro es aproximadamente 100 mil millones de masas solares. Nuestra distancia del centro es de 27,000 años luz.

75. (a) Usando la información en el problema anterior, ¿qué velocidad necesitas para escapar de la galaxia de la Vía Láctea desde nuestra posición actual? (b) ¿Necesitarías acelerar una nave espacial a esta velocidad en relación con la Tierra?

76. Las órbitas circulares en la ecuación 10.10 para las secciones cónicas deben tener excentricidad cero. A partir de esto, y utilizando la segunda ley de Newton aplicada a la aceleración centrípeta, muestra que el valor de α en la ecuación 10.10 viene dado por α = L²/GMm², donde L es el momento angular del cuerpo en órbita. El valor de α es constante y está dado por esta expresión independientemente del tipo de órbita.

77. Muestra que para la excentricidad igual a uno en la ecuación 10.10 para las secciones cónicas, la trayectoria es una parábola. Haz esto sustituyendo las coordenadas cartesianas, x e y, por las coordenadas polares, r y θ, y mostrando que tiene la forma general de una parábola, x = ay² + by + c.

78. Utilizando la técnica mostrada en Órbitas de satélite y Energía, muestra que dos masas m₁ y m₂ en órbitas circulares alrededor de su centro de masa común, tendrán energía total E = K + E = K₁ + K₂ - Gm₁m₂/r = Gm₁m₂/2r. Hemos mostrado la energía cinética de ambas masas explícitamente. (Sugerencia: Las masas orbitan en los radios r₁ y r₂, respectivamente, donde r = r₁ + r₂. Asegúrate de no confundir el radio necesario para la aceleración centrípeta con el de la fuerza de la gravedad).

79. Dada la distancia del perihelio, p, y la distancia del afelio, q, para una órbita elíptica, muestra que la velocidad en el perihelio, v_p, viene dada por



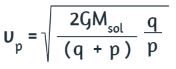
(Sugerencia: utiliza la conservación del momento angular para relacionar v_p y v_q, y luego sustitúyelo por la ecuación de conservación de la energía).

80. El cometa P/1999 R1 tiene un perihelio de 0.0570 UA y afelio de 4.99 UA. Usando los resultados del problema anterior, encuentra su velocidad en afelio. (Sugerencia: la expresión es para el perihelio. Usa la simetría para volver a escribir la expresión para afelio).

Problemas desafío

81. Se excava un túnel en el centro de un planeta perfectamente esférico y sin aire de radio R. Usando la expresión para g derivada en Gravitación cerca de la superficie de la Tierra para una densidad uniforme, muestra que una partícula de masa m caída en el túnel ejecutará un movimiento armónico. Deduce el período de oscilación de m y muestra que tiene el mismo período que una órbita en la superficie.

82. Siguiendo la técnica utilizada en Gravitación cerca de la superficie de la Tierra, encuentra el valor de g como una función del radio r del centro de un planeta esférico de densidad constante ρ con radios internos y externos R_in y R_out. Encuentra g para R_in < R_out y para r < R_in. Suponiendo que el interior de la corteza se mantiene sin aire, describa el recorrido dentro del planeta de corteza esférica.

83. Demuestra que la velocidad del área para una órbita circular de radio r alrededor de una masa M es ΔA/Δt = 1/2√GMr/. ¿Tu expresión da el valor correcto para la velocidad del área de la Tierra sobre el Sol?

84. Demuestra que el período de la órbita para dos masas, m₁ y m₁, en órbitas circulares de radios r₁ y r₂, respectivamente, sobre su centro de masa común, viene dado por



(Sugerencia: Las masas orbitan en los radios r₁ y r₂, respectivamente, donde r = r₁ + r₂. Usa la expresión para el centro de masa para relacionar los dos radios y observa que las dos masas deben tener momentos iguales pero opuestos. Comienza con la relación del período con la circunferencia y la velocidad de la órbita de una de las masas. Usa el resultado del problema anterior usando momentos en las expresiones de la energía cinética).

85. Demuestra que para pequeños cambios en la altura h, tal que h <:< R_E, la Ecuación 10.4 se reduce a la expresión ΔU = mgh.

86. Utilizando la Figura 10.9, dibuja cuidadosamente un diagrama de cuerpo libre para el caso de un péndulo simple que cuelga en la latitud λ, etiquetando todas las fuerzas que actúan sobre la masa puntual, m. Configura las ecuaciones de movimiento para el equilibrio, establece una coordenada en la dirección de la aceleración centrípeta (hacia P en el diagrama) y la otra sea perpendicular. Demuestra que el ángulo de deflexión ε, definido como el ángulo entre la cuerda del péndulo y la dirección radial hacia el centro de la Tierra, viene dada por la expresión siguiente. ¿Cuál es el ángulo de deflexión en latitud 45 grados? Asume que la Tierra es una esfera perfecta. tan (λ + ε) = g/(g - ω²R_E)tanλ, donde ω es la velocidad angular de la Tierra.

87. (a) Muestra la fuerza de marea en un objeto pequeño de masa m, definida como la diferencia en la fuerza de gravedad que se ejercería sobre m a una distancia en el lado cercano y el lado alejado del objeto, debido a la gravitación en una distancia R desde M, que viene dada por F_marea = 2GMm/R³Δr donde Δr es la distancia entre el lado cercano y el lado lejano y Δr << R. (b) Supongamos que caes de pies en el agujero negro en el centro de nuestra galaxia. Tiene una masa de 4 millones de masas solares. ¿Cuál sería la diferencia entre la fuerza en tu cabeza y tus pies en el radio de Schwarzschild (horizonte de eventos)? Supón que tus pies y cabeza tienen una masa de 5.0 kg y están separados 2.0 m. ¿Sobrevivirías pasando por el horizonte de eventos?

88. Encuentra las velocidades de transferencia de Hohmann, Δv_{Elipse-Tierra} y Δv_Elipse-Marte, necesarias para un viaje a Marte. Usa la ecuación 10.7 para encontrar las velocidades orbitales circulares para la Tierra y Marte. Usando la ecuación 10.4 y la energía total de la elipse (con semieje mayor a), dada por E = -GmM_s/2a, encuentra las velocidades en la Tierra (perihelio) y en Marte (afelio) que se requiere que estén en la elipse de transferencia. La diferencia, Δv, en cada punto es la aceleración de la velocidad o la velocidad de transferencia necesaria.