Respuestas - Capítulo IV
Comprueba tu aprendizaje
4.1 (a) Tomando la derivada con respecto al tiempo de la función de posición, tenemos v→(t) = 9.0t2i^ y v→(3.0 s) = 8.0i^ m/s
(b) Como la función de velocidad no es lineal, sospechamos que la velocidad promedio no es igual a la velocidad instantánea. Comprobamos esto y encontramos
v→prom = r→(t2) - r→(t1)/t2 - t1 = r→(4.0 s) - r→(2.0 s)/4.0 s - t2.0 s = (144i^ - 36.0i^)/2.0 s = 54.0i^ m/s,
que es diferente de v→(3.0s) = 81.0i^ m/s.
4.2 El vector de aceleración es constante y no cambia con el tiempo. Si a, b y c no son cero, entonces la función de velocidad debe ser lineal en el tiempo. Tenemos v→(t) = ∫v→dt = ∫(ai^ + bj^ + ck^)dt = (ai^ + bj^ + ck^)t m/s, ya que tomar la derivada de la función de velocidad produce a→(t). Si alguno de los componentes de la aceleración es cero, entonces ese componente de la velocidad sería una constante.
4.3 (a) Elije la parte superior del acantilado donde se arroja la roca desde el origen del sistema de coordenadas. Aunque es arbitrario, normalmente elegimos el tiempo t = 0 para que corresponda con el origen. (b) La ecuación que describe el movimiento horizontal es x = x0 + vxt. Con x0 = 0, esta ecuación se convierte en x = vxt. (c) Las ecuaciones 4.16 a 4.18 y la ecuación 4.19 describen el movimiento vertical, pero como y0 = 0 y v0y = 0, estas ecuaciones se simplifican enormemente para convertirse en y = 1/2(v0y + vy)t = 1/2vyt, vy = -gt, y = -1/2gt2, y vy2 = -2gy. (d) Usamos las ecuaciones cinemáticas para encontrar las componentes x e y de la velocidad en el punto de impacto. Usando vy2 = -2gy y observando que el punto de impacto es -100.0 m, encontramos que la componente y de la velocidad en el impacto es vy = 44.3 m/s. Nos da la componente x, vx = 15.0 m/s, v por lo que podemos calcular la velocidad total en el impacto: v = 46.8 m/s y θ = 71.3° por debajo de la horizontal.
4.4 El tiro de golf a 30°.
4.5 134.0 cm/s
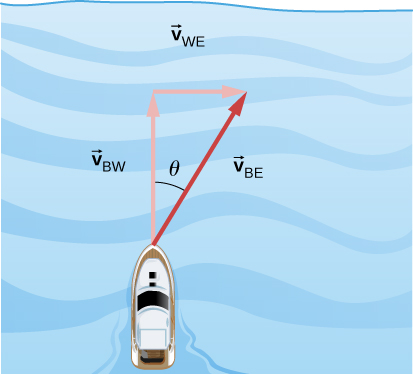
4.6 Etiquetar subíndices para la ecuación vectorial, tenemos B = bote, R = río y E = Tierra. La ecuación del vector se convierte en v→BE = v→BR + v→RE. Tenemos la geometría del triángulo rectángulo que se muestra en la Figura. Resolviendo para v→BE, tenemos = 71.3° por debajo de la horizontal.
v→BE = √v→BR2 + v→RE2/ = √3.02 + 4.52/
v→BE = 5.4 m/s, θ = tan−1(3.0/4.5) = 33.7°
Preguntas conceptuales
1. línea recta
3. La pendiente debe ser cero porque el vector de velocidad es tangente al gráfico de la función de posición.
5. No, los movimientos en direcciones perpendiculares son independientes.
7. a. no; b. mínimo en el vértice de la trayectoria y máximo en el lanzamiento y el impacto; c. no, la velocidad es un vector; d. sí, dónde aterriza
9. Ambos caen al suelo al mismo tiempo.
11. sí
13. Si va a pasar el balón a otro jugador, necesita mantener la vista en el marco de referencia en el que se encuentran los otros jugadores del equipo.
15.
Problemas
17. r→ = 1.0i^ - 4.0j^ + 6.0k^
19. Δr→ = 472.0i^ + 80.3j^
21. Suma de desplazamientos = -6.4 kmi^ + 9.4 kmj^
23 a. v→(t) = 8.0i^ + 6.0t2k^, v→(0) = 0, v→(1.0) = 8.0i^ + 6.0k^ m/s
b. v→prom = 4.0i^ + 2.0k^ m/s
25. Δr→1 = 20.00 mj^, Δr→2 = (2.000 × 104 m)(cos30°i^ + sen30°j^)
Δr→ = 1.700 × 104 mi^ + 1.002 × 104 mj^
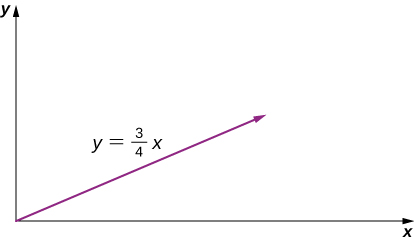
27. a. v→(t) = (4.0ti^ + 3.0tj^) m/s, r→(t) = (2.0t2i^ + 3/2t2j^) m,
b. x(t) = 2.0t2 m, y(t) = 3/2t2 m, t2 = x/2 ⇒ y = 3/4x
29. a. v→(t) = (6.0ti^ - 21.0t2j^ + 10.0t-3k^) m/s
b. a→(t) = (6.0i^ - 42.0tj^ - 30.0t-4k^) m/s2
c. v→(2.0 s) = (12.0i^ - 84.0j^ + 1.25k^) m/s
d. v→(1.0 s) = (6.0i^ - 21.0j^ + 10.0k^) m/s, |v→(1.0 s)| = 24.0 m/s
v→(3.0 s) = (18.0i^ - 189.0j^ + 0.37k^) m/s, |v→(3.0 s)| = 199.0 m/s
e. r→(3.0 s) = (3.0t2i^ - 7.0t3j^ - 5.0t-2k^) cm
31. a. v→(t) = -sen(1.0t)i^ + cos(t)j^ + k^
b. v→prom = 9.0i^ - 49.0j^ - 6.3k^ m/s
a→(t) = -cos(1.0t)i^ - sen(1.0t)j^
33. a. t = 0.55 s, b. x = 110 m
35. a. t = 0.24 s, d = 0.28 m, b. Ellos apuntan alto.
37. a. t = 12.8 s, x = 5619m. b. v→y = 125.0 m/s, v→x = 439.0 m/s, |v→| = 456.0 m/s
39. a. v→0y = 98.0 m/s, v→0 = 196.0 m/s.
b. h = 490.0 m.
c. v→0x = 169.7 m/s, x = 3394.0 m.
d. x = 2545.5 m, y = 465.5 m, s→ = 2545.5 mi^ + 465.5 mj^
41. −100 m = (−2.0 m/s)t − (4.9 m/s2)t2, t = 4.3s, x = 86.0 m
43. Rluna = 48 m
45. a. v→0y = 24 m/s, v→y2 = v→0y2 - 2gy ⇒ h = 23.4 m,
b. t = 3 s v0x = 18 m/s, x = 54 m,
c. y = -100 m, y0 = 0, y - y0 = v0yt - 1/2gt2 - 100 = 24t - 4.9t2 ⇒ t = 7.58 s,
d. x = 136.44 m
e. t = 2.0 s, y = 28.4 m, x = 36m
t = 4.0 s, y = 17.6 m, x = 22.4 m
t = 6.0 s, y = -32.4 m, x = 108 m
47. v0y = 12.9 m/s, y - y0 = v0yt - 1/2gt2 - 20.0 = 12.9t - 4.9t2
t = 3.7 s, v0x = 15.3 m/s ⇒ x = 56.7 m, entonces el tiro del golfista cae 13.3 m por debajo del green.
49. a. R = 60.8 m
b. R = 137.8 m
51. v→y2 = v→0y2 - 2gy ⇒ v→y = 2.9 m/s, y = 3.3 m/s
y = v→0y2/2g = (v→0senθ)2/2g ⇒ senθ = 0.91 ⇒ θ = 65.5°
53. R = 18.5 m
55. y = (tanθ0)x - [g/2(v0cosθ0)2]x2 ⇒ v0 = 16.4 m/s
57. R = v02sen 2θ0/g ⇒ θ0 = 15.0°
59. Le toma al receptor ancho 1.1 s para cubrir los últimos 10 m de su carrera.
Ttof = 2v0senθ/g ⇒ senθ = 0.27 ⇒ θ=15.6°
61. aC = 40 m/s2
63. aC = v2/r ⇒ v2 = raC = 78.4, v =8.85 m/s
T = 5.68 s, que es 0.176 rev/s = 10.6 rev/min
65. Venus está a 108.2 millones de km del Sol y tiene un período orbital de 0.6152 y,
r = 1.082 × 1011 m, T = 1.94 × 107 s
v = 3.5 × 104 m/s, aC = 1.135 × 10−2 m/s2
67. 360 rev/min = 6 rev/s
v = 3.8 m/s, aC = 144.m/s2
69. a. O'(t) = (4.0i^ + 3.0j^ + 5.0k^)t m
b. r→PS = r→PS' + r→S'S, r→(t) = r→'(t) + (4.0i^ + 3.0j^ + 5.0k^)t m,
c. v→(t) = v→'(t) + (4.0i^ + 3.0j^ + 5.0k^) m/s,
d. Las aceleraciones son las mismas
71.v→PC = (2.0i^ + 5.0j^ + 4.0k^) m/s
73. a. A = aire, S = gaviota, G = tierra
v→SA = 9.0 m/s velocidad de la gaviota con respecto al aire quieto
v→AG = ?, v→SG = 5 m/s, v→SG = v→SA + v→AG ⇒ v→AG = v→SG - v→SA
v→AG = -4.0 m/s
b. v→SG = v→SA + v→AG ⇒ v→SG = -13.0 m/s
t = -6000 m/-13.0 m/s = 7 min 42 s
75. Toma la dirección positiva en la misma dirección en que fluye el río, que está al este. S = orilla / tierra, W = agua y B = bote.
a. v→BS = 11 km/h, t = 8.2 min
b. v→BS = -5 km/h, t = 18 min
c. v→BS = v→BW + v→WS, θ = 22° al noroeste
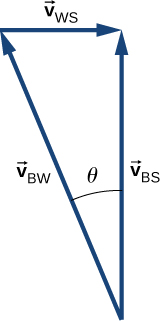
d. |v→BS| = 7.4 km/h, t = 6.5 min
e. v→BS = 8.54 km/h, pero solo la componente de la velocidad al otro lado del río se usa para obtener el tiempo
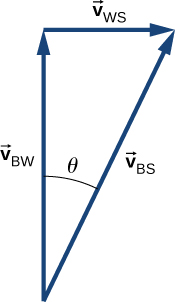
t = 6.0 min, Aguas abajo = 0.3 km
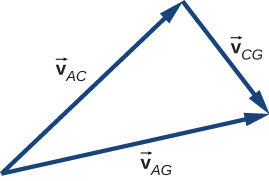
77. v→AG = v→AC + v→CG
|v→AC| = 25 km/h, |v→CG| = 15 km/h, |v→AC| = 29.15 km/h
el ángulo entre v→AC y v→AG es 31°, por lo que la dirección del viento es 14° al noreste.
Problemas adicionales
79. aC = 39.6 m/s2
81. 90.0 km/h = 25.0 m/s, 9.0 km/h = 2.5 m/s, 60.0 km/h = 16.7m/s
aT = -2.5 m/s2, aC = 1.86 m/s2, a = 3.1 m/s2
83. El radio del círculo de revolución en la latitud λ es REcosλ. La velocidad del cuerpo es 2πr/T
aC = 4π2REcosλ/T2 para λ = 40°, aC = 0.26%g
85. aT = 3.00 m/s2, v(5 s) = 15.00 m/s, aC = 150.00 m/s2, θ=88.8° con respecto a la tangente al círculo de revolución dirigido hacia el centro. |a→| = 150.03 m/s2
87. a→(t) = −Aω2cosωti^ − Aω2senωtj^
aC = 5.0 mω2, ω = 0.89 rad/s
v→(t) = -2.24 m/si^ - 3.87 m/sj^
89. r→1 = 1.5i^ + 4.0j^, r→2 = Δr→ + r→1 = 2.5i^ + 4.7j^ + 2.8k^
91. vx(t) = 265.0 m/s, vy(t) = 20.0 m/s, v→(5.0 s) = (265.0i^ + 20.0j^) m/s
95. v0 = 20.1 m/s
97. v = 3072.5 m/s, aC = 0.223 m/s2
Problemas de Desafío
99. a. -400 m = v0yt - 4.9t2
359.0 m = v0xt, t = 359.0/v0x - 400.0 = 359.0v0y/v0x - 4.9(359.0/v0x)2
v = 39.2 m/s
b. t = 12.0s
101. r→TC = (-32 + 80t)i^ + 50tj^, |r→TC|2 = (-32 + 80t)2 + (50t)2
2rdr/dt = 2(-32 + 80t) + 100tdr/dt = 2(-32 + 80t) + 100t/2r = 0
260t = 64 ⇒ t = 15 min
b. |r→TC| = 17 km






