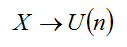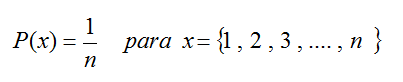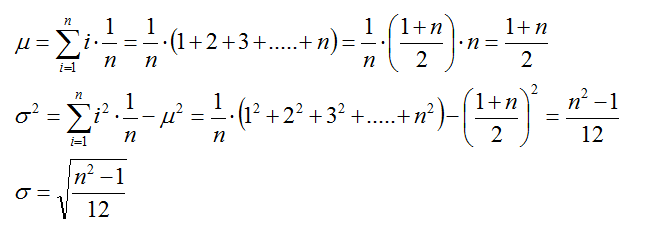Supongamos un experimento aleatorio en el que los
resultados posibles pueden tomar un conjunto de “n” valores
discretos y donde cualquiera de estos valores puede obtenerse con
igual probabilidad.
Es una distribución muy sencilla que asigna probabilidades iguales a un conjunto finito de puntos del espacio. Modeliza fenómenos en los que tenemos un
conjunto de n sucesos posibles, cada uno de los cuales con la misma
probabilidad de ocurrir. Si consideramos la variable aleatoria que
asigna cada uno de esos sucesos a un número natural desde 1 a
“n”, obtenemos lo que se denomina una distribución uniforme. El
único parámetro de la distribución es “n” de ahí que se suela
representar por:
Por ejemplo el lanzamiento de un dado correspondería a una distribución uniforme con n=6.
La función de probabilidad de una distribución uniforme viene dada por:
Los parámetros media, varianza y desviación típica de una distribución uniforme no son difíciles de obtener:
En la siguiente escena puedes observar
la función de probabilidad de la distribución Uniforme. Puedes
cambiar los diferentes parámetros que configuran dicha distribución y
observar como cambia esta función a medida que se varía alguno de
ellos. Extrae tus propias consecuencias. Así mismo puedes utilizar
también la escena como calculadora directa que permite resolver
situaciones particulares que se puedan plantear en problemas concretos.