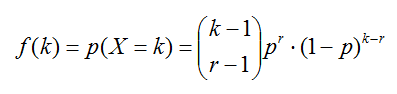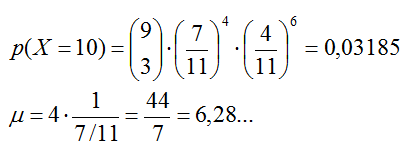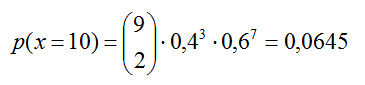4.4. Distribución binomial negativa.
Imagina una persona que está jugando al baloncesto con sus
amigos y que al finalizar el partido comienza a lanzar tiros libres.
A uno de ellos, especialmente desacertado, se le ocurre
comentar: ¡No pienso irme de aquí hasta conseguir anotar cinco canastas!
Esta
situación puede ilustrar bastante bien el problema que
resuelve la distribución binomial negativa.
Una
distribución binomial negativa de parámetros
"r" y
"p" surge como una secuencia infinita de intentos de tipo Bernoulli en los que:
- Cada secuencia es independiente de las otras.
- En cada intento solamente son posibles dos resultados (éxito o fracaso).
- La probabilidad de éxito es constante en cada secuencia.
- Los intentos continúan hasta que se consigan r éxitos.
Si llamamos X = “número de experimentos realizados hasta obtener el r-ésimo éxito”, diremos que la variable X sigue una distribución binomial negativa de parámetros r, p.
Es fácil deducir que la función de probabilidad de esta variable será:
La fórmula anterior no es difícil
de deducir. Piensa que para esta situación estamos seguros de que el
k-ésimo intento es un éxito y que en los k-1 intentos anteriores se
deben redistribuir los anteriores r-1 éxitos.
La distribución geométrica sería un caso particular de binomial negativa cuando r = 1.
Los parámetros media, varianza y desviación típica asociados a esta distribución serían:

EJEMPLO 1
Para tratar a un paciente de una afección de pulmón, han de ser
operados en operaciones independientes sus 5 lóbulos pulmonares. La
técnica a utilizar es tal que si todo va bien, lo que ocurre con
probabilidad de 7/11, el lóbulo queda definitivamente sano, pero si no
es así se deberá esperar el tiempo suficiente para intentarlo
posteriormente de nuevo. Se practicará la cirugía hasta que 4 de sus 5
lóbulos funcionen correctamente. ¿Cuál es el valor de
intervenciones que se espera que deba padecer el paciente? ¿Cuál es la
probabilidad de que se necesiten 10 intervenciones?
Este es un ejemplo claro de experimento aleatorio regido por una ley
binomial negativa, ya que se realizan intervenciones hasta que se
obtengan 4 lóbulos sanos, y éste es el criterio que se utiliza para
detener el proceso. Identificando los parámetros se tiene que si X= Número de operaciones hasta obtener r=4 con resultado positivo,
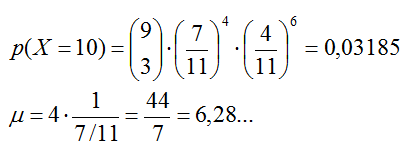
EJEMPLO 2:
Se sabe que la probabilidad de que un niño expuesto a una enfermedad
contagiosa la contraiga es de 0,4. Calcula la probabilidad de que el
décimo niño estudiado sea el tercero en contraer la enfermedad.
Podemos enfocar el problema como una binomial negativa de parámetros X = 10, k=3 y p=0,4
En la siguiente escena puedes observar
la función de probabilidad de la distribución Binomial negativa. Puedes
cambiar los diferentes parámetros que configuran dicha distribución y
observar como cambia esta función a medida que se varía alguno de
ellos. Extrae tus propias conclusiones. Así mismo, puedes utilizar
también la escena como calculadora directa que permite resolver
situaciones particulares que se puedan plantear en problemas concretos.