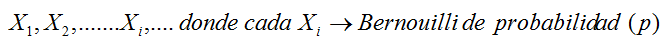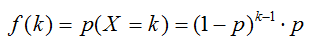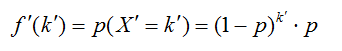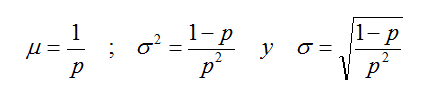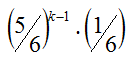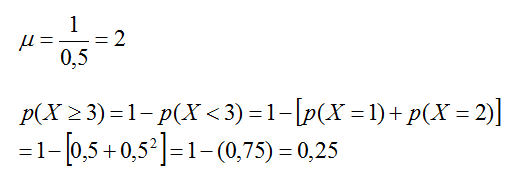Consideramos una sucesión de variables aleatorias independientes de
Bernouilli. Es decir una sucesión de pruebas independientes con dos
posibles resultados y con probabilidad de éxito constante e idéntica en
cada prueba.
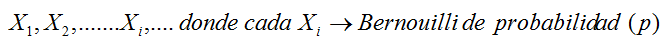
Esta sucesión como tal, al menos teóricamente, puede ser infinita.
Si consideramos la variable aleatoria
X = “nº de experiencias realizadas hasta obtener el primer éxito”, diremos que sigue una
distribución geométrica.
De acuerdo con la definición anterior, la variable X puede tomar valores desde uno en adelante. De este modo tenemos que la función de probabilidad para X, que es fácil de
deducir puesto que los primeros k-1 son fracasos y el k-ésimo éxito,
sería:
En algunos textos se considera la variable
“nº de fracasos obtenidos hasta el primer éxito”. En este caso el valor más pequeño que puede tomar la variable es cero y la formulación cambia un poco.
Los parámetros media, varianza y desviación típica de esta distribución vienen dados por:
EJEMPLO 1:
Supongamos que queremos hacer un estudio sobre la variable
aleatoria referente al número de veces que un jugador necesita para
poder efectuar la salida en el juego del parchís. Hay que recordar que, en este
juego, un jugador no comienza el mismo hasta obtener un 5 al lanzar el
dado.
Podría ocurrir que solamente necesitara:
- Una tirada X = 1; con probabilidad 1/6
- Dos tiradas X = 2 con probabilidad (5/6)(1/6)
- Tres tiradas X =3 con probabilidad (5/6)(5/6)(1/6)
-
...
-
"k" tiradas X = k con probabilidad
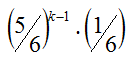
La variable puede seguir tomando valores indefinidamente puesto que es
posible encontrar a un jugador cuya “mala suerte“ haga que
NUNCA obtenga el dichoso 5.
Estaríamos ante el caso de una distribución geométrica de parámetro 1/6.
EJEMPLO 2:
Un matrimonio quiere tener una hija, y por ello deciden tener hijos
hasta el nacimiento de la esperada hija. Calcular el número esperado de
hijos (entre varones y hembras) que tendrá el matrimonio. Calcular la
probabilidad de que la pareja acabe teniendo tres hijos o más.
En la siguiente escena puedes observar
la función de probabilidad de la distribución Geométrica. Puedes
cambiar los diferentes parámetros que configuran dicha distribución y
observar como cambia esta función a medida que se varía alguno de
ellos. Extrae tus propias consecuencias. Así mismo puedes utilizar
también la escena como calculadora directa que permite resolver
situaciones particulares que se puedan plantear en problemas concretos.
En el siguiente vídeo podemos asistir a una clase sobre la distribución geométrica:
Vídeo enlazado desde YouTube, licencia de YouTube estándar