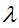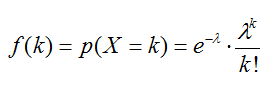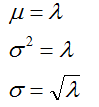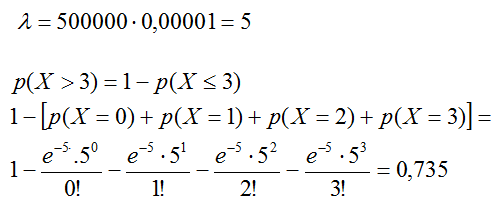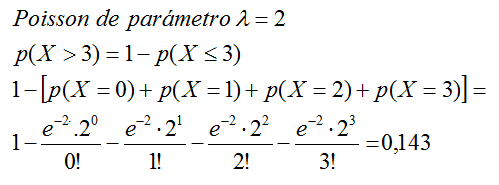Hay ocasiones en las que un
proceso que podría encuadrarse dentro de lo que conocemos como
distribución binomial, ofrece dificultades que en ocasiones incluso
hacen inviable la resolución de un problema. En este sentido, pensemos
el caso en que la constante
“p”, probabilidad de éxito de
un experimento de Bernouilli sea muy pequeña; (lo que
habitualmente se denominan casos muy raros), o bien el caso en que los
cálculos que se derivan de la fórmula de la binomial sean tan
farragosos que saquen de rango nuestra calculadora. Sería importante
disponer de otra alternativa más interesante.
Por otro lado, pensemos también en situaciones en las que los elementos
de la población pueden considerarse extraordinariamente numerosos,
(coches que pasan durante un tiempo por una autopista, metros de tela
de una producción en una fábrica, individuos de un país susceptibles de
padecer cierta enfermedad, entre otros ejemplos posibles.
Un proceso de Poisson se presenta en relación con un acontecimiento
(éxito) durante un periodo de tiempo o espacio. Se conoce que el número
de éxitos en la unidad de estudio, instante temporal o espacial
determinado es
y a su vez este es independiente del número de éxitos en otro instante o espacio. Si llamamos X =
“nº de éxitos obtenidos en un determinado periodo ”. Diremos que X sigue una
distribución de Poisson.
La función de probabilidad de esta variable viene determinada por la fórmula:
Los parámetros media, varianza y desviación típica de esta distribución vienen dados por:
EJEMPLO 1 :
Cierta enfermedad tiene probabilidad de ocurrir p=1/100000, lo que en
Medicina se denomina prevalencia. Calcula la probabilidad de que en
una ciudad de 500000 habitantes haya más de 3 personas con dicha
enfermedad. ¿Cuál sería en dicha ciudad el número de enfermos esperado?
Solución:
El problema se podría abordar mediante una B( 500000, 0,00001 )
En este caso aproximaremos por un modelo de Poisson de parámetro
EJEMPLO 2:
En una carretera se producen un promedio de 2 accidentes anuales.
Calcula la probabilidad de que este año se produzcan más de 3
accidentes.
En la siguiente escena puedes observar
la función de probabilidad de la distribución de Poisson. Puedes
cambiar los diferentes parámetros que configuran dicha distribución y
observar como cambia esta función a medida que se varía alguno de
ellos. Extrae tus propias consecuencias. Así mismo puedes utilizar
también la escena como calculadora directa que permite resolver
situaciones particulares que se puedan plantear en problemas concretos.