Si el proceso consistía en una serie de extracciones o selecciones ello implicaba la reposición de cada extracción o selección, o bien la consideración de una población muy grande (cartas en un casino). Sin embargo, si la población es pequeña y las extracciones no se remplazan, las probabilidades no se mantendrán constantes. La distribución hipergeométrica viene a cubrir esta necesidad de modelar procesos de Bernouilli con probabilidades no constantes (sin reemplazamiento).

La distribución hipergeométrica es especialmente útil en todos aquellos casos en los que se extraigan muestras o se realicen experiencias repetidas sin devolución del elemento extraído o sin retornar a la situación experimental inicial.
Es una distribución fundamental en el estudio de muestras pequeñas de poblaciones pequeñas y en el cálculo de probabilidades de juegos de azar. Tiene grandes aplicaciones en el control de calidad para procesos experimentales en los que no es posible retornar a la situación de partida.
Las consideraciones a tener en cuenta en una distribución hipergeométrica:
- El proceso consta de "n" pruebas, separadas o separables de entre un conjunto de "N" pruebas posibles.
- Cada una de las pruebas puede dar únicamente dos resultados mutuamente excluyentes.
- El número de individuos que presentan la característica A (éxito) es "k".
- En la primera prueba las probabilidades son: P(A)= p y P(A)= q; con p+q=1.
En estas condiciones, se define la variable aleatoria X = “nº de éxitos obtenidos”. La función de probabilidad de esta variable sería:

La media, varianza y desviación típica de esta distribución vienen dadas por:
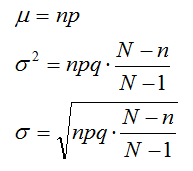
EJEMPLO 1:
Supongamos la extracción aleatoria de 8 elementos de un conjunto formado por 40 elementos totales (cartas baraja española) de los cuales 10 son del tipo A (salir oro) y 30 son del tipo complementario (no salir oro).
Si realizamos las extracciones sin devolver los elementos extraídos y llamamos X al número de elementos del tipo A (oros obtenidos) que extraemos en las 8 cartas; X seguirá una distribución hipergeométrica de parámetros 40 , 8 , 10/40.H(40,8,0,25).
Para calcular la probabilidad de obtener 4 oros:

EJEMPLO 2:
De cada 20 piezas fabricadas por una máquina, hay 2 que son defectuosas. Para realizar un control de calidad, se observan 15 elementos y se rechaza el lote si hay alguna que sea defectuoso. Vamos a calcular la probabilidad de que el lote sea rechazado.

Cuando N es muy grande, como criterio se suele considerar N > 10n, la distribución hipergeométrica se puede aproximar por la binomial B( n, p ) con p = k/N.