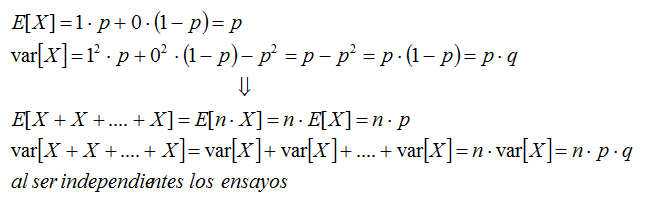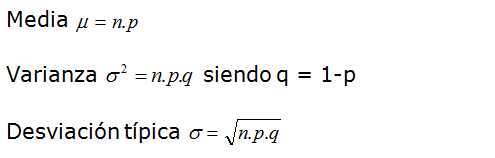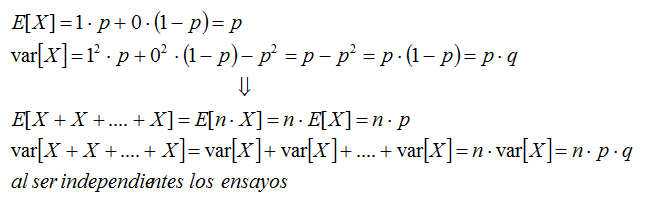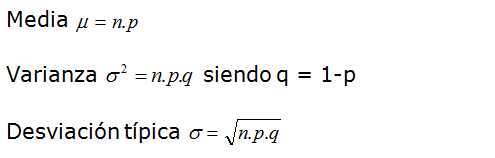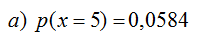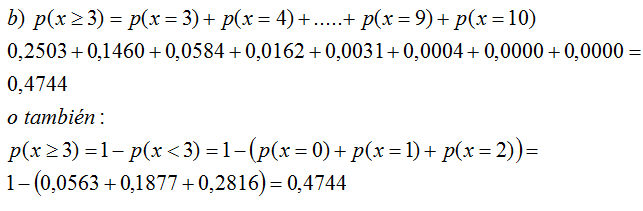3.2. Parámetros de la distribución binomial. tabulación.
3.2.1. Esperanza matemática,varianza y desviación típica de la binomial
Consideramos la variable aleatoria X que sigue una binomial B(n,p).
Recordamos que la variable aleatoria X expresa el número de éxitos que
se obtienen al realizar "n" pruebas o ensayos independientes de
Bernouilli con probabilidad "p" de éxito y "(1-p)" de fracaso. Esta
variable puede interpretarse perfectamente como suma de "n" variables
de Bernouilli, una por cada uno de los ensayos realizados. En
consecuencia, para deducir la esperanza matemática y la varianza de la
binomial B(n,p) podemos calcular la esperanza matemática y varianza de
la variable correspondiente a un ensayo y después aplicar las
propiedades generales de dichos parámetros con respecto a la suma de
variables independientes.
Para un ensayo:
Por tanto:
3.2.2. Tabulación de la binomial
Aunque las calculadoras científicas
realizan sin ningún tipo de problema los cálculos que se derivan de la
función de probabilidad de cualquier distribución binomial, hasta hace
relativamente poco tiempo dichos cálculos resultaban muy largos y
engorrosos, por este motivo se realizaron tabulaciones para las
distribuciones binomiales más habituales y a ellas se recurría para determinar de la
forma más aproximada posible los valores concretos del problema
particular. En dichas tablas se podía localizar la probabilidad de
"r" éxitos de una varriable aleatoria B(n,p), sin más que
encuadrar la columna de la probabilidad y la fila relativa al número de
pruebas.
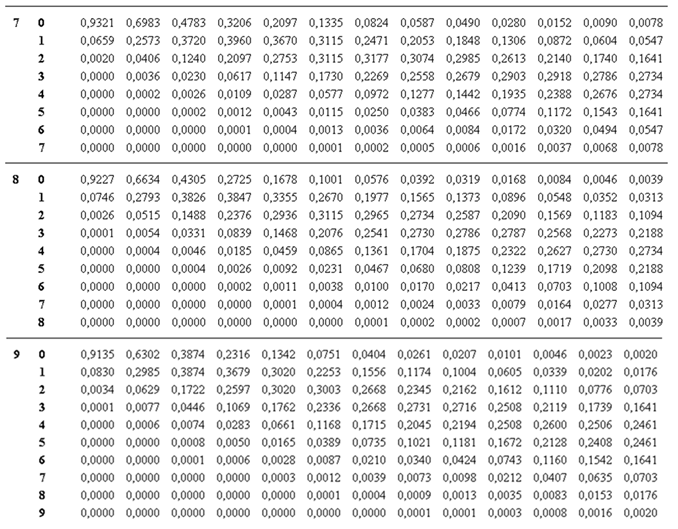
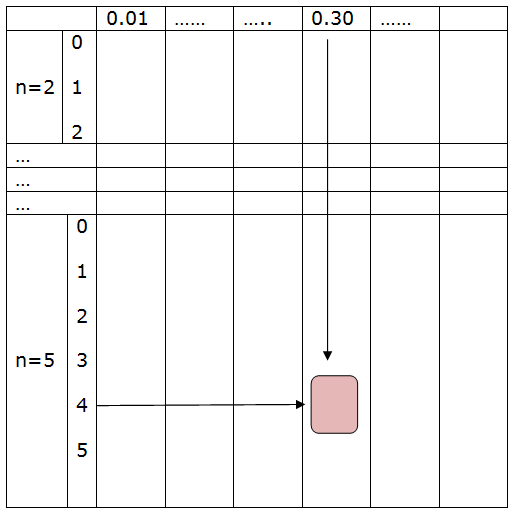
Por ejemplo si quiero calcular para la B(5,0.3) La probabilidad de 4 éxitos. Miraré la tabla como se indica en la figura:
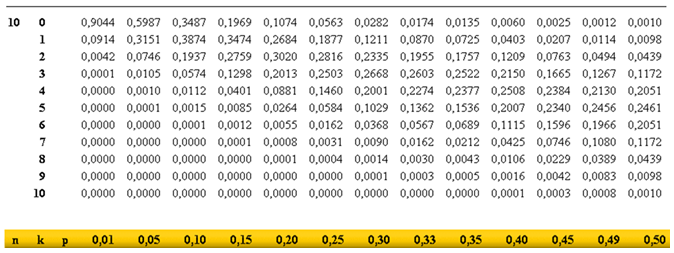
Existen tablas muy extensas para las
binomiales. La más popular era la que condensaba en una página todas
las binomiales de hasta n=10 y distintas probabilidades comprendidas
entre un valor mínimo 0,01 y un máximo de 0,5 con paso de 0,05. Aquí
puedes ver dicha tabla.
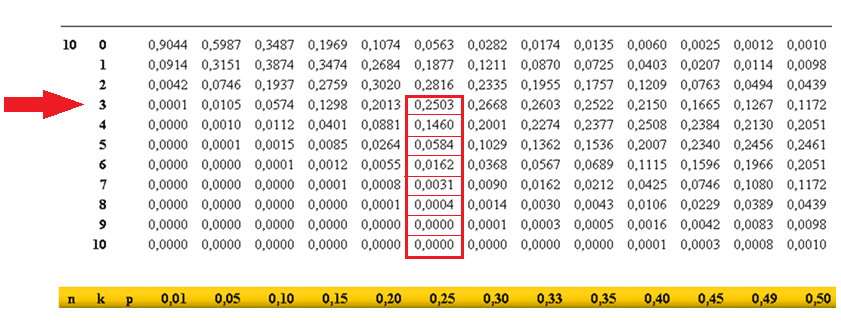
EJEMPLO:
Vamos a utilizar la tabla para resolver una situación sencilla.
Supongamos que Ramona realiza un examen tipo test de 10 preguntas con
cuatro opciones cada una de las que sólo una es correcta. Si responde
de forma aleatoria a todas las preguntas. Calcula:
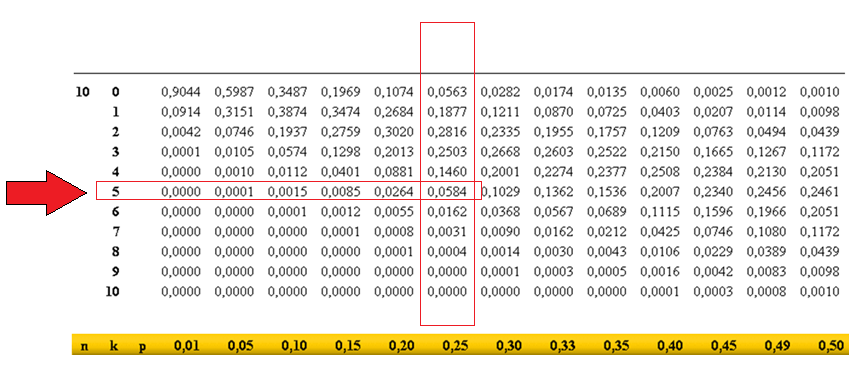
a) Probabilidad de contestar 5 preguntas bien.
b) Probabilidad de contestar bien al menos 3 preguntas.
El problema evidentemente se puede enmarcar en una binomial de parámetros n=10 y p=0,25
En el siguiente vídeo podemos asistir a una clase sobre la distribución binomial:
Vídeo enlazado desde YouTube, licencia de YouTube estándar