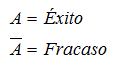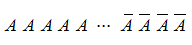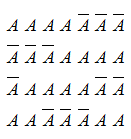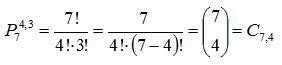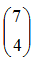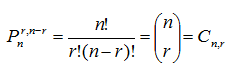La distribución binomial constituye un
modelo de probabilidad teórico al que se adaptan multitud de
situaciones y problemas de la vida real. Conviene por tanto profundizar en este modelo teórico para así poder transferir
los resultados a las distintas situaciones concretas.
En este sentido se pueden deducir la función de probabilidad asociada a una distribución binomial.
Si consideramos una distribución
B(n,p). en la que denominamos:
Uno de los casos en los que se obtienen "r" éxitos sería:
Es decir primero "r" éxitos y después "n-r" fracasos.
Particularizando a 4 éxitos y 3 fracasos, para ayudarnos en la
deducción, existirían muchas situaciones en las que podría presentarse
el suceso cuatro éxitos y tres fracasos, por ejemplo:
En realidad en las agrupaciones anteriores vemos dos elementos
distintos, uno se repite 4 veces y otro 3. Esta situación es una
vieja conocida en combinatoria. Hablamos de las agrupaciones de 7
elemenos en los que uno se repite 4 veces y otro 3, esto es:
Permutaciones con repetición de 7 elementos en los que uno se repite 4
veces y otro 3. El número de permutaciones de este tipo vendría dado
por:
Es decir que todos los casos posibles en los que se presentan cuatro éxitos y tres fracasos sería el número combinatorio:
En general, la expresión para todos los casos en los que se pueden presentar " r" éxitos y "n-r" fracasos sería:
Teniendo en cuenta que la probabilidad de éxito es "p" y la de fracaso
"(1-p)" y la independencia de cada prueba, deducimos que la función que
nos permite calcular la probabilidad de que la variable aleatoria X
(número de éxitos obtenidos en n pruebas), sería:
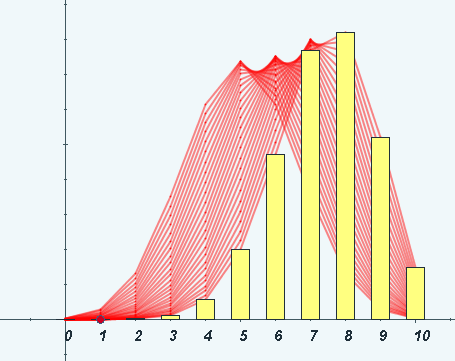
En la siguiente escena puedes observar las representaciones gráficas de
distintas distribuciones binomiales. Puedes cambiar los valores de la
binomial que coinciden con los controles "n" y "p". Observa cómo cambia la forma de la gráfica y
extrae tus propias conclusiones.