Un experimento aleatorio se conoce como
de Bernouilli cuando solamente da lugar a dos resultados posibles
complementarios entre sí: Éxito y fracaso.
Por ejemplo:
- Personal favorable o no a cierto candidato.
- Pieza defectuosa o no en un control de calidad.
- Infectado o no por un virus.
Las características que debe reunir un experimento para considerarse una distribución binomial son:
- En cada prueba que se realice solamente son posibles dos resultados; Éxito y Fracaso.
- El resultado de cada prueba es independiente de las anteriores.
- La probabilidad de éxito se mantiene constante en cada prueba.
Si consideramos la variable
X que representa
el número de éxitos obtenidos en n pruebas realizadas, se dice que esta variable sigue una distribución binomial de parámetros n y p.
(B(n,p)).
Para la simulación de modelos de
probabilidad como por ejemplo el modelo de una distribución binomial
existe un artefacto muy simple y con bastantes aplicaciones didácticas
como es el aparato de Galton.
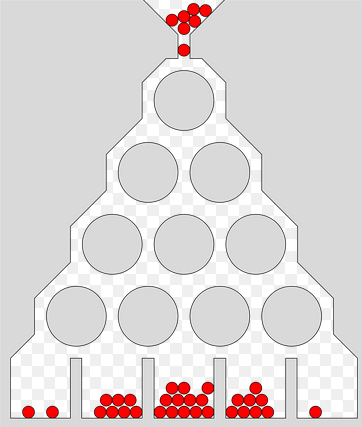
Un aparato de Galton está constituido por un conjunto variable de pisos
huecos con topes. En el primer piso hay un sólo tope, en el segundo
dos, en el tercero tres y así sucesivamente. Si dejamos que una bola
caiga desde el primer piso, al chocar con cada tope puede ir a la
derecha o a la izquierda. En principio si no se hace nada especial en
el tope, la probabilidad de ir a la izquierda es la misma que la de ir
a la derecha. En la simulación del aparato de Galton que aparece en la
escena siguiente vemos que estas probabilidades las podemos cambiar con lo que en
realidad en dicha escena simulamos toda una familia de aparatos de Galton (ventajas del mundo virtual). Al final de los pisos, cuyo número también es
variable en la escena, aparecen una especie de canales contenedores
para recoger las bolitas.
Mediante este sencillo aparato Galton simulaba de forma práctica modelos teóricos de probabilidad.
Si observamos el recorrido de una bola en el aparato de Galton . En
cada bifurcación la bola puede ir a la izquierda con probabilidad
"p" o a la derecha con probabilidad
"q=1-p".
La variable aleatoria que toma valor 0 si cae a la izquierda o 1 si cae
a la derecha se llama de Bernouilli y la variable X que da el número de
unos al finalizar el experimento (lugares a la derecha) se denomina
binomial. Los posibles valores de esta variable dependen del número de
pisos que tiene el aparato de Galton, lo cual puedes comprobarlo en la escena.
Si lanzamos una detrás de otra "n" bolitas al final del
recorrido caerán en los distintos canales formando una determinada
figura que si repites el experimento varias veces verás que
"caprichosamente" se vuelve a formar casi la misma figura. Es decir
estamos obteniendo una aproximación de lo que denominamos una
distribución de probabilidades.
Manipula la siguiente escena cambiando los controles y conjeturando y
comprobando sobre los canales de más o menos probabilidad. Cambia
también el control que en principio aparece con valor por defecto de
1/2. Podrías simular modelos para el lanzamiento de dados, cartas, o
cualquier otra experiencia en la que aparezcan solamente dos resultados
posibles: éxito (bola que va a la derecha) y fracaso (bola que va a
la izquierda).

