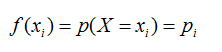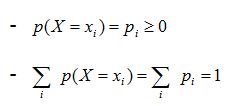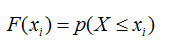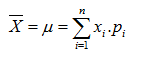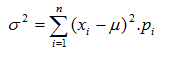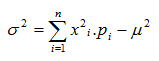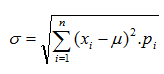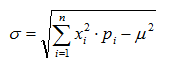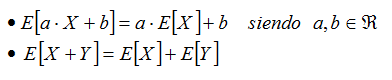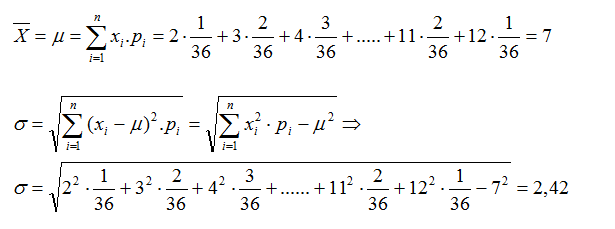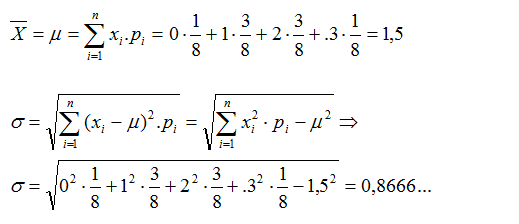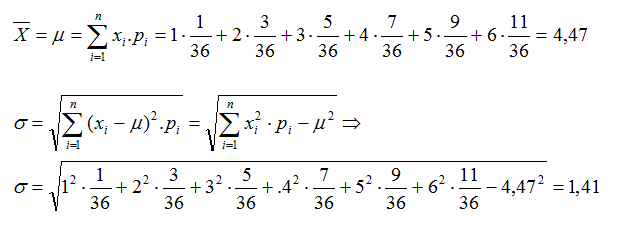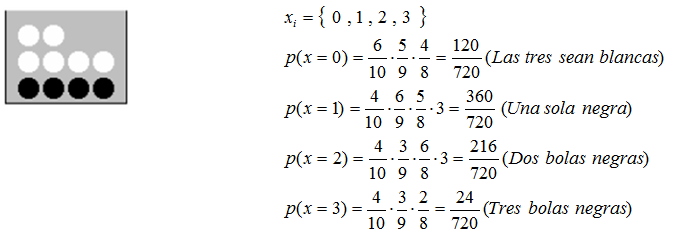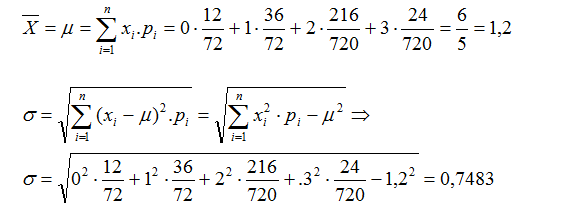2. Función de probabilidad. Propiedades y parámetros asociados
En cualquier variable aleatoria discreta se puede definir una función particular denominada
función de probabilidad que asocia a cada valor de la variable la probabilidad de que dicha variable tome ese valor.
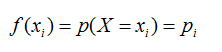
De la propia definición se desprende que para que una función sea función de probabilidad se debe cumplir que:
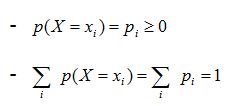
A partir de la función de probabilidad se puede definir la denominada
función de distribución como:
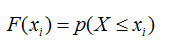
PARÁMETROS ASOCIADOS
Se denominan así a ciertos valores numéricos de alguna manera
resumen los datos y carácterísticas de la variable aleatoria
- Media aritmética o esperanza matemática
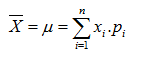
- Varianza
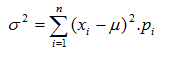
Para el cálculo práctico de la varianza en problemas concretos se
suele recurrir a esta otra fórmula a la que se llega desarrollando el
cuadrado de la anterior y que resulta mucho más sencilla para el
cálculo directo
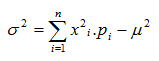
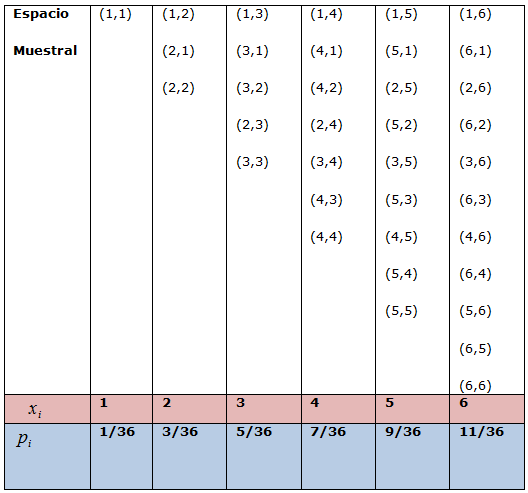
- Desviación típica
A partir de la fórmula de la varianza y para solventar el
problema de que el parámetro venga dado en las mismas unidades de
medida que los datos de la variable se define la desviación típica como:
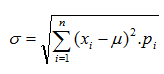
De la misma forma que antes, para el cálculo práctico directo se suele utilizar:
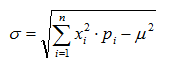
PROPIEDADES
Las propiedades más interesantes de la media o esperanza matemática y
de la varianza son las que tienen relación con el comportamiento
de estos parámetros con respecto a la suma y producto por un escalar de
variables aleatorias.
- Propiedades de la esperanza matemática
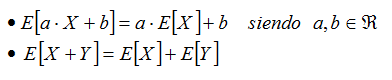
- Propiedades de la varianza

EJEMPLO 1:
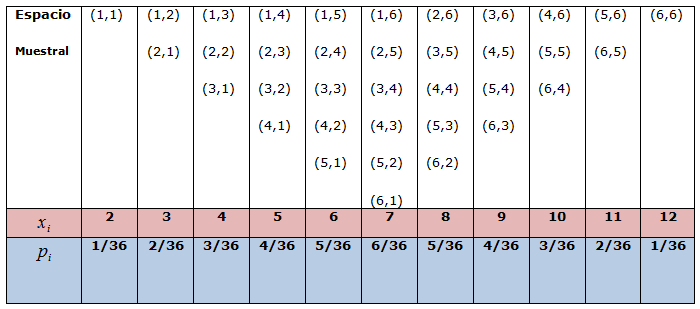
Consideramos el experimento consistente en lanzar dos dados y observar
las caras superiores. En este experimento la variable aleatoria que
definimos sería la que asigna a cada suceso la suma de las puntuaciones
de las caras superiores.
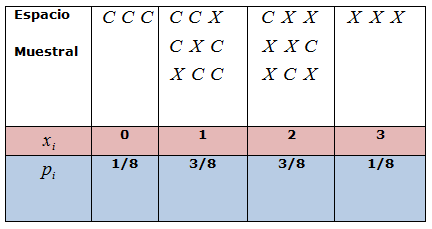
EJEMPLO 2:
Consideramos el experimento consistente en el lanzamiento de tres
monedas y la variable que asocia a cada suceso el número de cruces
obtenidas.
EJEMPLO 3:
Consideramos el experimento consistente en lanzar dos dados y la
variable que asigna a cada suceso la mayor de las puntuaciones
obtenidas.
EJEMPLO 4
Extracción de tres bolas de una urna que contiene 6 bolas blancas y 4
negras. Si consideramos la variable aleatoria número de bolas negras
extraídas.
En la siguiente escena aparecen el
diagrama de barras para frecuencias relativas del lanzamiento de dos
dados un total de veces que puedes modificar mediante el control
"nº de veces". Puedes manipular dicho control y observar
qué ocurre cuando se aumenta o disminuye, además puedes hacer la
comparación con el modelo teórico de su función de probabilidad,
representada de forma gráfica. Intenta extraer tus propias
conclusiones.