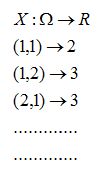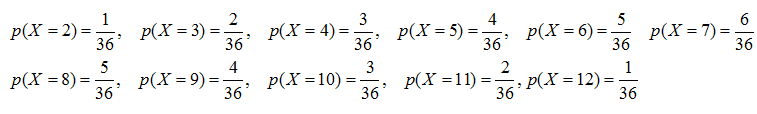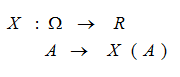1. Concepto de variable aleatoria.

El concepto de variable aleatoria viene a dotar de una mayor potencia matemática y de un mejor manejo y utilización del heterodoxo mundo de los espacios muestrales ya que traslada el experimento a función y la ocurrencia o no de un suceso con la posibilidad de que la función tome o no unos determinados valores numéricos.
Como veremos más adelante existirán también modelos de variables aleatorias teóricos que podrán adaptarse perfectamente a multitud de problemas prácticos y que simplificarán mucho el tratamiento y solución de dichas situaciones. En este sentido veremos la importancia sobre todo de la distribución binomial.

Supongamos que lanzamos dos dados cúbicos. El espacio muestral formado por los posibles resultados estaría compuesto por:

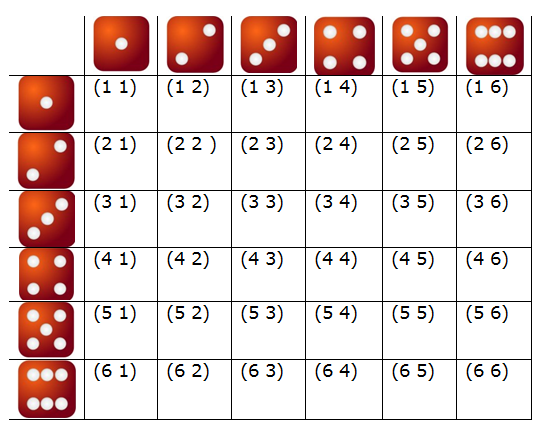
Si consideramos una función que asocie a cada resultado posible del experimento la suma de los resultados de las caras superiores obtenidas; esta función podría tomar los valores desde 2 hasta 12.

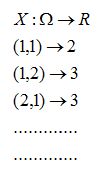
Además se puede asociar a cada valor de la variable la probabilidad de que tome dicho valor;


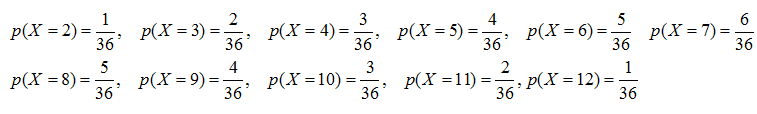
CONCEPTO DE VARIABLE ALEATORIA

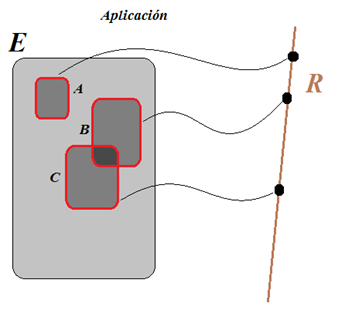
Se define una variable aleatoria como una función que asocia a cada suceso de un espacio muestral un número real.

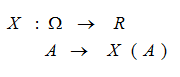
Según sean los valores del recorrido de esta función, (X(A)), podemos clasificar las variables aleatorias en:

• DISCRETAS: Cuando el recorrido toma valores aislados.
• CONTINUAS: Cuando el recorrido puede tomar al menos teóricamente cualquier valor de un intervalo de la recta real.

Una variable aleatoria continua es aquella que toma valores en un conjunto continuo (en toda la recta real, en un intervalo o en una unión de intervalos)
Si dado un gran número de observaciones se construye un histograma con intervalos de clase de longitud pequeña, se obtiene una gráfica que intuitivamente tiende a una curva cada vez que aumenta el número de observaciones, reduciendo la longitud de las clases del histograma.

• Supongamos que se nos ocurre el experimento aleatorio consistente en preguntar a los alumnos de un determinado instituto por el tiempo que tardan en desplazarse desde su casa al centro. La variable aleatoria en este caso vendría determinada por un intervalo de tiempo en el que al menos teóricamente podría tomar cualquier valor entre 0 y 25 minutos aproximadamente.
• Supongamos que se nos ocurre como experimento aleatorio salir a la calle y aleatoriamente preguntar a las personas el dinero que se han gastado en las últimas rebajas. La variable aleatoria en este caso vendría determinada por una gran diversidad de valores dentro de posiblemente también un intervalo bastante grande (0, ...).