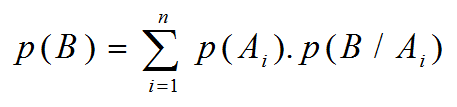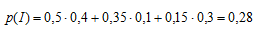6. Teorema de la probabilidad total
Mediante este resultado, se hace
presente la clásica afirmación "divide y vencerás". Nos preguntamos
globalmente por la probabilidad de que ocurra un suceso y contestamos a
partir del conocimiento que tenemos de las distintas probabilidades de
que ocurra dicho suceso cuando han ocurrido otros que en realidad
completan todo el espacio muestral.
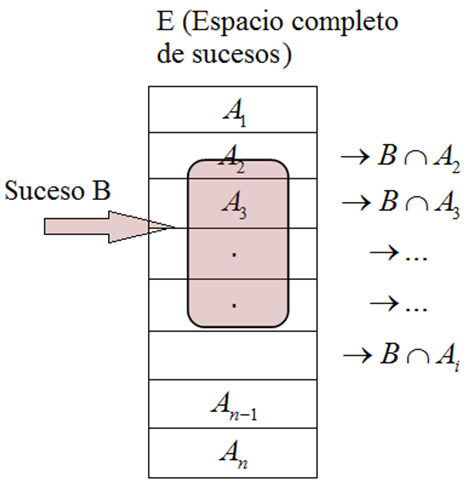
Formalmente; supongamos que A1, A2, A3, .....An,
constituyen un sistema completo de sucesos para el espacio muestral E
asociado al experimento aleatorio considerado. Supongamos también que B
es un suceso cualquiera de l espacio E, para el cuál se conocen
las probabilidades p(B/Ai) .
En estas condiciones podemos deducir que:
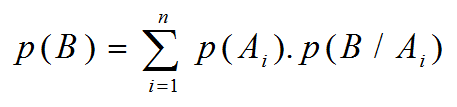

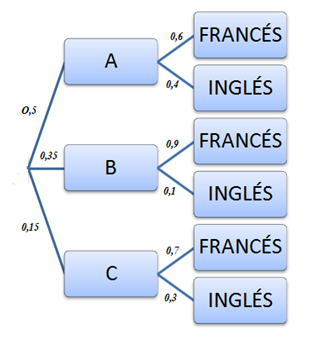
Por ejemplo; la clásica situación que se
presenta en los centros de secundaria. Imagina un IES que dispone de
tres modalidades mutuamente excluyentes de bachillerato y de dos
idiomas, inglés y francés. La modalidad A la cursa el 50% de los
alumnos, la B el 35% y la C el 15%. Se sabe también que eligen francés
el 60% de los de la modalidad A, el 90% de los de B y el 70% de los de
C. ¿Cuál será la probabilidad de que elegido un alumno al azar estudie
inglés.
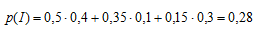
En la siguiente escena puedes practicar con la probabilidad condicionada y aplicar el Teorema de la probabilidad total.