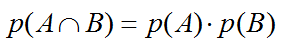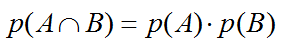Imagina que vamos a sacar dos cartas de una baraja. Realizamos el experimento sacando en primer lugar una de las cartas, anotamos su valor, la devolvemos a la baraja, mezclamos bien y extraemos la segunda carta. ¿Influye lo que ocurrió en la primera extracción en lo que ocurirá en la segunda?.
En muchas situaciones en la que la probabilidad aparece ligada a sucesos compuestos, la ocurrencia de un suceso no influye en nada en la ocurrencia o no del otro. Por así decirlo, no existe nada adicional que modifique las posibilidades de ocurrencia del segundo suceso cuando se sabe que ha ocurrido el primero; esto es si el primero no hubiera ocurrido, las posibilidades del segundo seguirían siendo exactamente las mismas. En estos casos, se habla de Independencia de los sucesos.
Cuando se cumpla que p(B/A) coincida con p(B) se dice que los sucesos A y B son independientes. En este caso la probabilidad de la intersección obtenida en el epígrafe anterior quedaría simplemente como  el producto de las probabilidades de cada suceso.

La fórmula anterior se conoce con el nombre de criterio de independencia y es lo que en la práctica nos lleva a calificar sucesos como independientes.

En el siguiente vídeo puedes recabar algunas ideas sobre sucesos independientes y dependientes.

Y otro vídeo en el que se trata el tema de las predicciones.