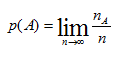4. Concepto de probabilidad

La idea de probabilidad es uno de esos conceptos que cualquier ser humano tiene preaprendiido. Todos tenemos conocimiento intuitivo de lo que supone que una cosa sea muy difícil  que ocurra (acertar en la lotería) o de  algo que sea más fácil que ocurra (lanzar una moneda y que salga cara). Otra cosa es la definición matemática. Desde el punto de vista formal, el concepto de probabilidad  se puede abordar desde tres puntos de vista diferentes.

La probabilidad de un suceso A de un experimento aleatorio se puede definir como el número al que se aproximan las frecuencias relativas de dicho suceso cuando el experimento se repite un número indefinido de veces.

4.2. Definición de Laplace

Si un espacio muestral consta de un número finito de sucesos simples y todos ellos tienen la misma posibilidad de suceder (equiprobables). Se define la probabilidad de cualquier suceso A como:


 

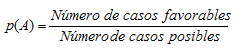4.3. Definición de Kolmogorov

Si un espacio muestral consta de un número finito de sucesos simples y todos ellos tienen la misma posibilidad de suceder (equiprobables). Se define la probabilidad de cualquier suceso A como: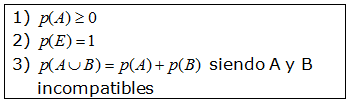


Como primeras consecuencias y propiedades de la definición axiomática tenemos:

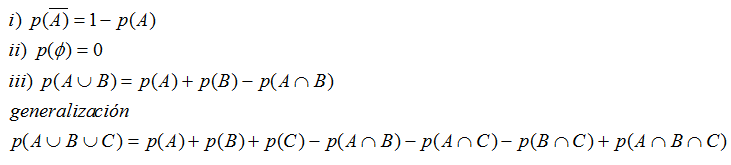Que se expresan como: • La probabilidad del suceso contrario a A es uno menos la probabilidad de A. • La probabilidad del suceso imposible es cero. • La probabilidad de dos sucesos compatibles es la suma de las probabilidades de cada uno menos la de la intersección. Esta propiedad se puede generalizar a más de dos sucesos.

En el siguiente vídeo puedes recabar algunas ideas sobre la probabilidad.

En la siguiente escena puedes comprobar la probabilidad teórica con la experiencia práctica. La idea es ver como la repetición del juego se aproxima a la idealización teórica.