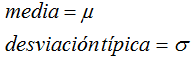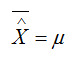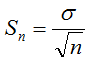El teorema central del límite es sin
duda el resultado más importante relacionado con el muestreo y las
distribuciones en el muestreo de las medias muestrales y de las
proporciones muestrales. Este resultado tiene muchas versiones. Una de
las más simples es la que sigue:
TEOREMA CENTRAL DEL LÍMITE
Si X es una variable aleatoria de una población con media y desviación típica
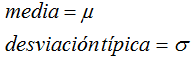
Entonces se verifica:
a) La distribución de las medias muestrales de tamaño
“n” tiene:
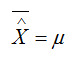
y por desviación típica
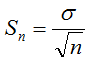
b) Además la distribución de las medias muestrales se aproxima cada vez más a la distribución normal.
Entendiendo por aproximarse a la normal que:
1) Si se sabe que la población de partida es normal
entonces sea cual sea el tamaño de las muestras, la distribución de las
medias muestrales será una distribución normal.
2) Si la población de partida no es normal, la
distribución de las medias podrá aproximarse a la normal con ciertas
garantías para un tamaño muestral mayor o igual que 30.
En las siguientes escenas puedes
comprobar la tesis del teorema central del límite en tres casos de
distribuciónes de partida. el primer caso sobre una población de
partida normal, el segudo con una distribución de partida no normal
sesgada a la derecha y en el tercer caso partiendo de una distribución
uniforme.
Comprueba como a medida que se aumenta el control tamaño muestral
y se afina la partición, la tendencia hacia la normalidad de la
distribución de las medias muestrales.