Supongamos también que extraemos muestras de tamaño “n” de dicha población. Cada muestra proporcionará una determinada media (media muestral). Si consideramos cada una de estas medias como valores de una variable aleatoria podemos estudiar su distribución, a lo que llamaremos distribución muestral de medias o distribución en el muestreo de las medias muestrales.
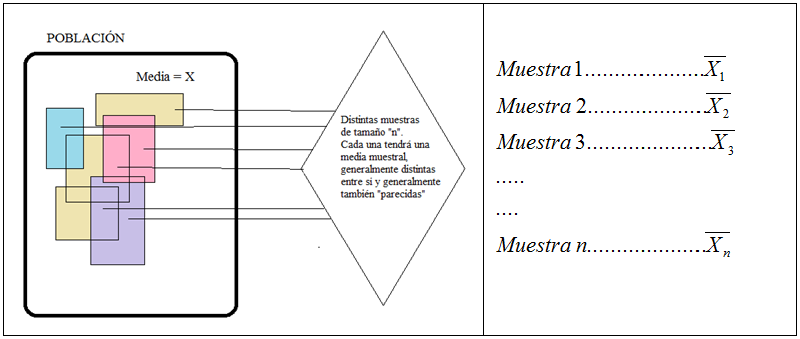
Llamamos a la variable aleatoria que toma los distintos valores de las medias muestrales de tamaño "n"
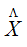
Las características principales de esta variable aleatoria son:
- La media es la misma que la de la población.
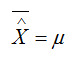
- La desviación típica es la misma que la de la población dividida entre la raíz de n;
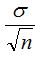
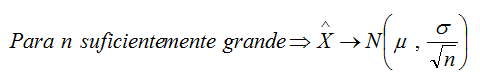
En el siguiente vídeo podemos observar los conceptos generales de distribuciones en el muestreo.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
EJEMPLO :
Las puntuaciones de un test de inteligencia para adultos siguen una distribución Normal de media 100 y desviación típica 16. Si extraemos una muestra aleatoria simple de 25 individuos:
a) Calcula la probabilidad de que la media muestral sea inferior a 95
b) Probabilidad de que esté comprendida entre 98 y 102
Solución:
Se dan las características en la población para poder asegurar que las medias muestrales siguen:
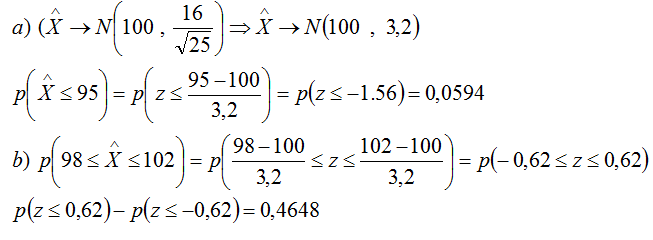
En la siguiente escena puedes observar
como se distribuyen las medias muestrales. Puedes manipular el control
<<Tamaño muestral>> y observar como influye en el
reagrupamiento o dispersión de datos en la distribución normal.
Para el caso en que la población de partida no sea normal, puedes observar las escenas finales del siguiente epígrafe, (Teorema central del límite).
Para el caso en que la población de partida no sea normal, puedes observar las escenas finales del siguiente epígrafe, (Teorema central del límite).
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
