3. Distribución en el muestreo de la proporción

Supongamos una población de la que conocemos la proporción “p” de individuos que cumple cierta característica. Si de esta población extraemos muestras de tamaño “n”, y en cada muestra a su vez estudiamos la proporción de individuos que cumple la característica estudiada, obtendremos diferentes proporciones muestrales:
De manera que si llamamos
 a la variable aleatoria formada por los distintos valores que toman  las proporciones muestrales. Esta variable aleatoria como tal tiene las siguientes características:

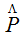
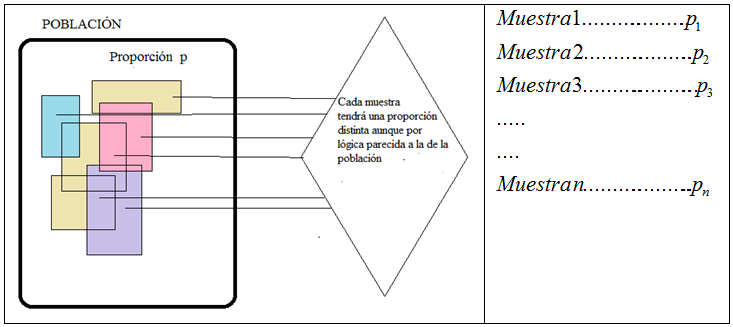
• La media o esperanza matemática de la variable "proporciones muestrales" es la proporción poblacional  “p”
  
• La desviación típica de la variable de la variable "proporciones muestrales" es:
  
  

Además a medida que crece el tamaño n , la distribución de las proporciones muestrales se aproxima cada vez más a la DISTRIBUCIÓN NORMAL (siempre que "p" no esté muy próxima a 0 ni a 1)


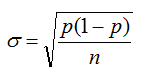
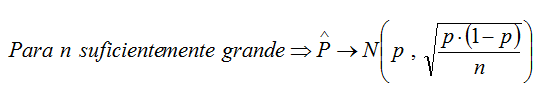
EJEMPLO:
En una población se conoce que un 2% de la misma es favorable a la construcción de un centro de rehabilitación para toxicómanos. Si suponemos que en un barrio de la misma viven 500 personas. Calcula la probabilidad de encontrar en dicho barrio más de 9 personas favorables a la construcción de dicho centro.