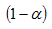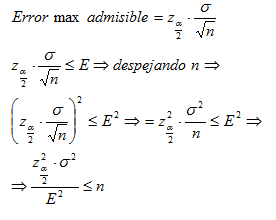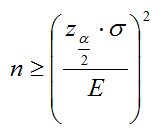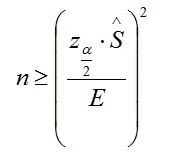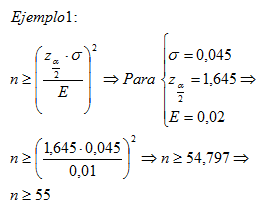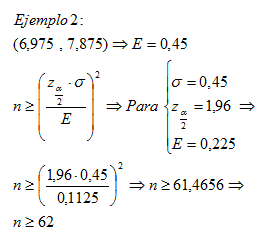Consideremos dos nuevas situaciones:
- Se conoce de estudios anteriores, que el tiempo de reacción de los conductores se distribuye de forma normal con una desviación típica de 0,045 segundos. Si se quiere estimar el tiempo de reacción medio con un error máximo admisible de 0,01 segundos con un nivel de confianza del 90% . ¿Qué tamaño mínimo debería tener la muestra aleatoria sobre la que tendríamos que trabajar?
- Las notas de selectividad de una signatura se distribuyen de forma normal con una desviación típica de 0,45. Supongamos que después de realizar un intervalo de confianza para estimar la nota media en selectividad de los alumnos de una ciudad se obtuvo que este intervalo era (6,975, 7,875) con un nivel de confianza del 95%. Si consideramos que el margen de error del intervalo es demasiado grande y nos interesaría reducirlo a la mitad. ¿Cuántos individuos debería tener la nueva muestra aleatoria aleatoria para reducir a la mitad el error máximo admisible manteniendo el mismo nivel de confianza?
Estas situaciones y otras muchas que se podrían plantear conducen al cálculo de un tamaño mínimo de muestra a partir del cual se cumplan determinadas condiciones en nuestra estimación de un parámetro poblacional como la media.
De la propia formulación del intervalo se observa que el tamaño que debe exigirse para una muestra depende fundamentalmente del nivel de confianza que se desee para los resultados, de la amplitud del intervalo de confianza o error máximo que se esté dispuesto a admitir y de la desviación típica poblacional o de la cuasi-desviación típica de la muestra en caso de que no se conozca aquella. Fijados estos, simplemente despejando algebraicamente en las fórmulas, podemos calcular el tamaño mínimo de la muestra que debe utilizarse para cumplir con las premisas estipuladas.
Así pues para un nivel de confianza