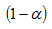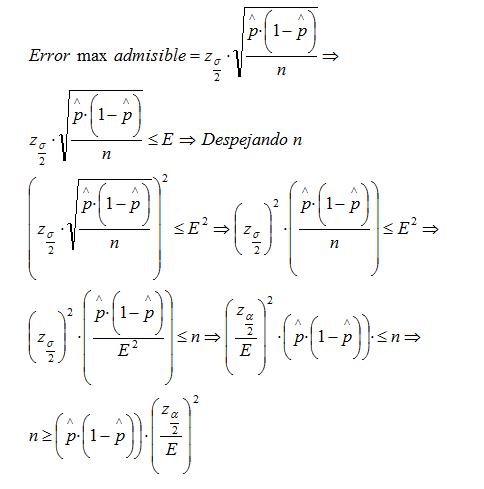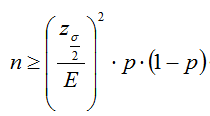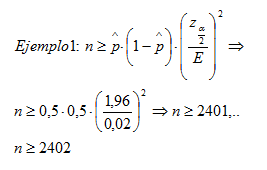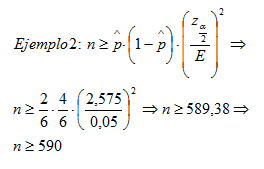- Supongamos que se quiere estimar la proporción de individuos de una ciudad que tienen más de 60 años. Para realizar el trabajo debemos seleccionar de forma aleatoria una muestra de tamaño "n". La pregunta que nos hacemos es cuál debe ser el valor mínimo de muestra que debe considerarse para garantizar que con un nivel de con fianza del 95% el error de estimación, radio de nuestro intervalo de confianza, no supere el 2%. Como en este caso no disponemos de información alguna sobre posibles valores aproximados de proporción, debemos suponer el caso más desfavorable que sería p = 0,5.
- Supongamos que tenemos un dado ligeramente cargado del que sospechamos que la proporción de salir cinco es 2/6. ¿Cuántas veces debemos lanzarlo y anotar el resultado para que con un nivel de confianza del 99% el error de nuestra estimación no supere el 5%?
Existen otras muchas situaciones en las que es importante la localización de un tamaño muestral mínimo a partir del cual se cumplan determinadas condiciones en nuestra estimación.
De la propia formulación del intervalo se observa que el tamaño que debe exigirse para una muestra depende fundamentalmente del nivel de confianza que se desee para los resultados y de la amplitud del intervalo de confianza, (error máximo), que se esté dispuesto a admitir. Fijados estos, y simplemente despejando algebraicamente en las fórmulas, podemos calcular el tamaño mínimo de la muestra que debe utilizarse para cumplir con las premisas estipuladas.
Para un nivel de confianza