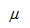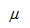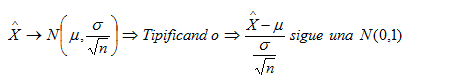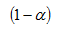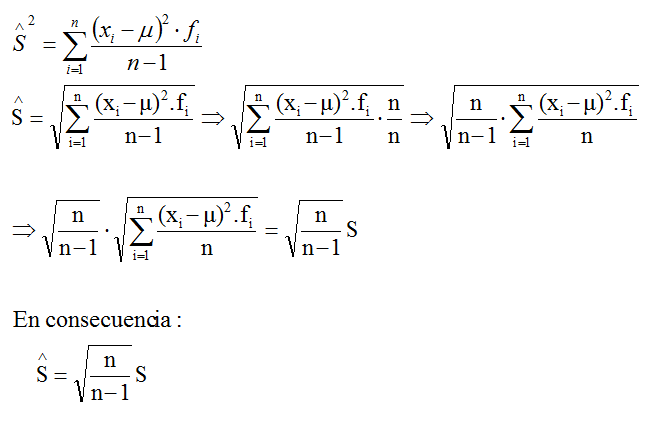3.3. Intervalo de confianza para la media con desviación típica desconocida.
Supongamos una población en la que queremos estimar la media poblacional desconocida que denominaremos
Consideremos también que extraemos una muestra aleatoria simple
de tamaño “n” en la que obtenemos un valor concreto para la media
muestral. Sabemos que si la población de partida es normal o el
tamaño de la muestra es mayor de 30, la distribución en el muestreo de
las medias muestrales sigue una normal de parámetros :
Pero nos encontramos con el problema de que la desviación típica de la
población también es desconocida. Algunos autores optan directamente
por considerar como sustituto de la desviación típica de la población,
la desviación típica muestral. Nosotros optamos en este caso por otro
procedimiento como es sustituir la desviación típica poblacional
desconocida por la cuasidesviación típica muestral. Otros autores optan
por procedimientos más depurados y complicados como el que puedes ver
en el siguiente vídeo.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
Razonando de la misma forma que en el caso anterior, una vez hecha la sustitución de:
En esta distribución pueden calcularse los valores que encierran una probabilidad de
Simplemente mirando y deduciendo en la tabla de la normal N(0,1)
El cálculo de la cuasivarianza y
cuasidesviación típica aparece como tecla directa en cualquier
calculadora científica. La definición de estas medidas y su
relación con la varianza y desviación típica habituales se especifican
en el siguiente desarrollo:
En la siguiente escena al pulsar <<genera muestra>> se selecciona una muestra aleatoria de la población tomando como parámetros el tamaño y nivel de confianza indicados en los campos de texto así etiquetados y se dibuja el intervalo de confianza indicando sus extremos. Si se cambia el tamaño de la muestra, ésta es completamente nueva y consecuentemente se observa como el intervalo cambia significativamente. Si lo que cambiamos es el nivel de confianza la muestra no varía y lo que acontece es una ligera variación en la longitud del intervalo, los cambios son menos significativos.