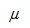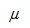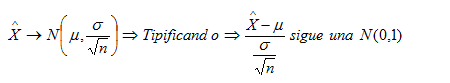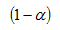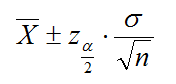3.2. Intervalo de confianza para la media con desviación típica poblacional conocida
Supongamos una población en la que queremos estimar la media poblacional desconocida que denominaremos
por ejemplo la estatura media de los alumnos de primaria de una
ciudad. Supongamos también que extraemos una muestra aleatoria simple
de tamaño “n” en la que obtenemos un valor concreto para la media
muestral. Sabemos que si la población de partida es normal o el
tamaño de la muestra es mayor de 30, la distribución en el muestreo de
las medias muestrales sigue una normal de parámetros:
En esta distribución pueden calcularse los valores que encierran una probabilidad de
Simplemente mirando y deduciendo en la tabla de la normal N(0,1)
EJEMPLO RESUELTO:
En una muestra de 400 bolsas de frutos secos de los que
habitualmente se venden en el mercado, se obtuvo que el peso medio de
las mismas fue de 102 gramos. Se sabe de otros estudios que la
desviación típica poblacional del peso de este tipo de artículo es de 2
gramos. Estima un intervalo de confianza a un nivel del 90% para
la media poblacional del peso de la bolsa de frutos secos
En el siguiente vídeo podemos ver una clase sobre el intervalo de confianza para la media con desviación típica poblacional conocida.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
En la siguiente escena puedes observar
cómo los intervalos de confianza que se calculan van cubriendo o no a
la verdadera media poblacional. Puedes cambiar el tamaño de la
muestra y el nivel de confianza modificando los respectivos controles.
Observa como al modificar estos controles, cambia la longitud del
intervalo y el número de los que cubren al parámetro poblacional. La
escena tiene un límite de 100 intervalos de confianza. También permite calcular todos los intervalos de forma continua si
pulsas el control de <<animar>>