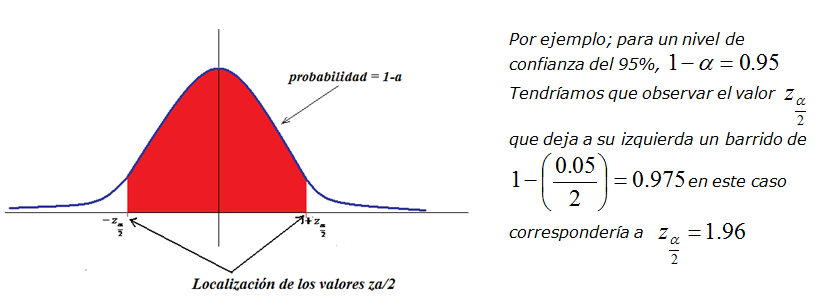
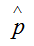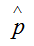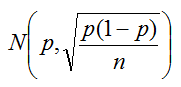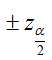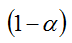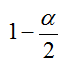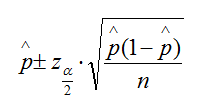bastaría con ir a la tabla de la normal y localizar el valor que deja un barrido a su izquierda de
(de aquí la notación empleada). Por ejemplo, para calcular los
valores críticos asociados a un nivel de confianza del 95% se razonaría:
De forma más o menos intuitiva podemos decir que:
En la siguiente escena puedes observar
como los intervalos de confianza que se calculan, van cubriendo o no a
la verdadera proporción poblacional. Puedes cambiar el tamaño de la
muestra y el nivel de confianza modificando los respectivos controles.
Observa como al modificar estos controles, cambia la longitud del
intervalo y el número de estos que cubren al parámetro poblacional. La
escena tiene un límite de 100 intervalos de confianza. La escena
permite también realizar todos los intervalos de forma continua si
pulsas el control de <<animar>>