3. Intervalos de confianza

La idea global de la estimación mediante un intervalo de confianza es la siguiente. Supongamos que quiero estimar un parámetro poblacional, generalmente la media poblacional o la proporción poblacional desconocidos ambos. La población global es inabordable por diversos motivos logísticos, por ejemplo puede ser muy numerosa o que económicamente el proceso sea muy caro. Consideramos por tanto la extracción de una muestra aleatoria, por ahora que creamos lo suficientemente grande como para que los parámetros obtenidos en dicha muestra sean parecidos a lo que debería ocurrir en la población. Un intervalo de confianza es considerar dos valores de manera que se tenga cierto nivel de certeza (confianza) de que el verdadero valor del parámetro poblacional se encuentre entre los que determinan nuestro intervalo.
Por ejemplo, cuando decimos que en un estudio hecho por una empresa se estimó que la estatura media de los jóvenes españoles oscila entre 172 cm y 178 cm, y que el trabajo se realizó con un nivel de confianza del 95%, entendemos que la verdadera estatura media poblacional será seguramente un valor comprendico entre los dos anteriores y que la probabilidad de que el intervalo [172, 178] realmente cubra a la verdadera estatura media es de 0.95. 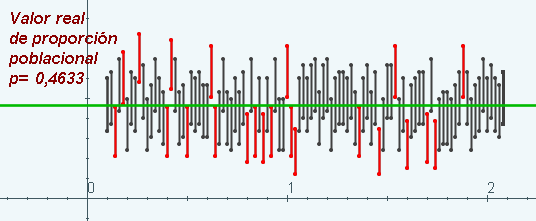Entendiendo esto último como que si realizamos la estimación por ejemplo 100 veces, con la elección de 100 muestras aleatorias distintas, aproximadamente 95 de nuestras respuestas en forma de intervalos de confianza cubriran al verdadero valor del parámetro estatura media poblacional. ¿Será nuestra respuesta [172, 178] uno de estos intervalos, digamos buenos? Hay un 95% de posibilidades de que sí.