2. Estimación. Estimación puntual y estimación por intervalos

Al proceso mediante el cuál inferimos valores de parámetros poblacionales a partir de los resultados obtenidos en una muestra extraida aleatoriamente se denomina estimación.
Si realizamos dicha estimación asignando un valor muestral concreto al parámetro poblacional que se desea estimar, estaremos ante una estimación puntual.

En general, se verifica que cualquier parámetro poblacional que se quiera estimar tiene siempre en la muestra su estadístico paralelo:

Media poblacional... Media muestral
Varianza poblacional... Varianza muestral

En los estudios estadísticos se pueden utilizar diferentes estimadores para un mismo parámetro. Dos de las características  principales que poseen los estimadores son el sesgo y la eficiencia.

• Un estimador se denomina insesgado o centrado, si su media coincide con el valor del parámetro poblacional que se va a estimar
• Un estimador se dice eficiente cuando su varianza es mínima

Por ejemplo, para estimar una media poblacional se pueden elegir entre los estadísticos: media aritmética muestral, mediana muestral o moda muestral. La pregunta que nos haríamos es cuál de ellos sería el “mejor”. Tanto la media muestral como la mediana muestral son estimadores insesgados, sin embargo, la varianza de la media muestral es menor que la de la mediana muestral. Los estimadores centrados o insesgados más precisos son aquellos que tienen menor desviación típica.
Existe toda una teoría en estadística que aborda el tema de la estimación puntual y que excede los objetivos de este estudio. Nuestro objetivo se centra en otro tipo de estimación. La estimación por intervalos.

Supongamos que para realizar una estimación de un parámetro poblacional, un profesor encarga la tarea a un  grupo de diez alumnos. Estos a su vez seleccionan diez muestras aleatorias sobre las que calculan los correspondientes estadísticos muestrales. Evidentemente estos estadísticos no tienen por qué coincidir. Nuestro problema consiste ahora en elegir de entre los diez el que “creamos” mejor como estimador del parámetro poblacional. ¿Cómo actuamos?¿Cuál elegimos?
La estimación puntual es poco útil como aproximación del parámetro poblacional que se desea estimar ya que solamente proporciona un valor concreto, el cual además varía con cada elección de la muestra. Desde el punto de vista estadístico, es mucho más interesante no concretar un valor sino obtener un intervalo dentro del cuál se tiene cierta confianza de que se encuentre el parámetro poblacional desconocido y objeto principal de nuestra estimación.


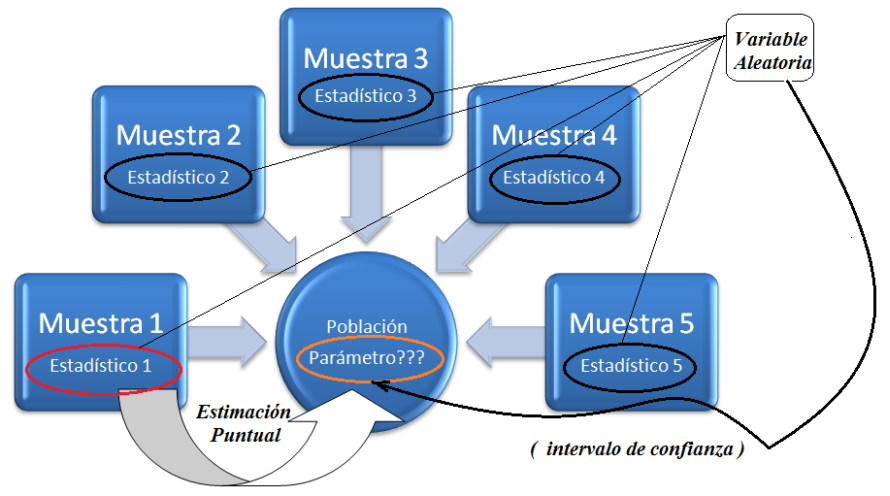
En este sentido, definimos los siguientes conceptos:

• Estimador por intervalo: Par de valores de estadísticos que se utilizan para estimar el parámetro poblacional. (como variables aleatorias que son tendrán su correspondiente distribución en el muestreo)
• Estimación por intervalo: Valores numéricos concretos que toma el estimador por intervalo para una muestra determinada.
  
• Coeficiente de confianza o nivel de confianza: Es la probabilidad de que un estimador por intervalo cubra el verdadero valor del parámetro poblacional que se estima. Generalmente se representa
  
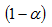
• Nivel de significación o de riesgo: Es la diferencia entre la certeza y el nivel de confianza deseado, es decir
  
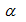
• Valor crítico: Es el valor de la abscisa que deja a su derecha un área igual a la mitad del nivel de significación. Se representa habitualmente mediante
  
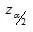
• Margen de error: Es la diferencia entre los extremos superior e inferior de un intervalo de confianza.
• Error máximo admisible: Radio del intervalo de confianza