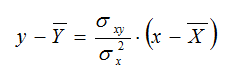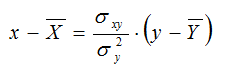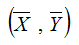Como se ha mencionado anteriormente, en los casos en los que se observe
cierto grado de correlación lineal, intentaremos aproximar la nube de
puntos mediante una recta. A estas líneas se les llaman
rectas de regresión. Dependiendo
del procedimiento de minimización de distancias que se emplee, bien sean verticales u
horizontales, y utilizando el procedimiento de mínimos
cuadrados obtendremos dos tipos de recta:
-
Recta de regresión de Y sobre X
-
Recta de regresión de X sobre Y
Como puedes observar se trata de las clásica expresión de una
recta en su forma punto pendiente.
La obtención de las expresiones de las rectas anteriores no es
sencilla. Como características fáciles de
descubrir podemos señalar que el signo de la pendiente depende
únicamente de la covarianza en ambas expresiones y que ambas pasan por
el punto común:
En la siguiente escena puedes practicar con el cálculo de todos los
parámetros relacionados con la regresión en variables bidimensionales.
Puedes introducir los datos que desees seleccionando previamente las
filas que necesites (máximo de 36). Sigue las instrucciones y podrás
comprobar el valor de todos los parámetros y la representación gráfica
de la nube de puntos y de las dos rectas de regresión.
Es importante que practiques y construyas tablas tú mismo y que la
escena te sirva de apoyo y comprobación de resultados. También
convendría que supieras utilizar tu calculadora y usarla en los
problemas prácticos. En este sentido, ten en cuenta que lo que puede
variar en cada calculadora es la introducción de los datos. Una vez que
conozcas este procedimiento, el resto suele ser muy parecido. Como
ejemplo, recordar el caso de la calculadora DESCARTES (ver el apartado 4.1).
Realiza algún ejercicio de regresión utilizando la calculadora para variable bidimensional de DESCARTES.
En el siguiente video puedes asistir a una clase sobre regresión lineal
Vídeo enlazado desde YouTube, licencia de YouTube estándar
En la siguiente escena puedes manipular la nube de puntos y observar
como varía el ajuste por mínimos cuadrados y como cambian las rectas de
regresión.
Escena desarrollada por Juan Jesús Cañas Escamilla y José R. Galo Sánchez
(RED Descartes)
Una de las primeras acciones que se
realizan en cualquier estudio estadístico es la depuración de los
datos, localizando y decidiendo si los elementos anómalos que se denominan en la literatura científica como "outliers" o
valores atípicos, deben tenerse en cuenta en la realización del estudio
o no. Esta escena sirve para analizar la influencia que puede tener la
variación de un solo dato en un análisis estadístico, en concreto en la
regresión lineal.
En la escena aparece una nube de puntos, el número de ellos se puede
elegir mediante el control "número de puntos". A veces la
nube aparece muy dispersa y aunque es posible realizar un ajuste lineal
las conclusiones estadísticas serían muy poco o nada fiables, pero
puede cambiarse sin más que pulsar el botón "Inicio". Uno de los puntos es un control gráfico que puede moverse y desplazarse a voluntad utilizando los dos controles situados abajo o
directamente pulsando y arrastrando. Con el botón "ver rectas" se observa la solución global del problema.
Mediante el botón "ver tabla" se pueden observarse los datos reales del problema.
Con el botón ""ver parámetros" puedes ver todos los parámetros calculados y necesarios para el modelo de regresión.
También se dispone de un botón para ver cómo varía el ángulo de las dos
rectas y otro para un gráfico que relaciona el coeficiente de
correlación y el ángulo al desplazar el punto variable.
Escena desarrollada por Juan Jesús Cañas Escamilla y José R. Galo Sánchez
(RED Descartes)
