El término desviación típica fue incorporado a la estadística porKarl Pearsonen 1894. la principal ventaja que representa la desviación típica respecto a la varianza es que su unidad de medida es la misma que la de los datos. Esto hace mucho más sencilla la posible interpretación.
Es una medida del grado de dispersión de las observaciones alrededor de su valor medio. La desviación típica se define como la raíz cuadrada positiva de la varianza. Tiene el mismo cometido que ésta y además la ventaja de que las unidades en las que se mide son las mismas que las de los datos de la distribución. Puede considerarse la medida de dispersión por excelencia y aparece como tecla o función directa en cualquier calculadora o programa estadístico.
Si partimos de la definición de varianza, la fórmula para el cálculo de la desviación típica sería:
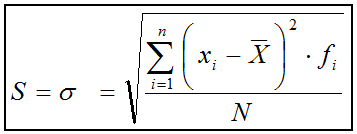
De la misma forma que en el apartado
anterior. Si desarrollamos y simplificamos la expresión anterior se
llega a otra mucho más simple que es la que se utiliza en la práctica y
cuya expresión es:
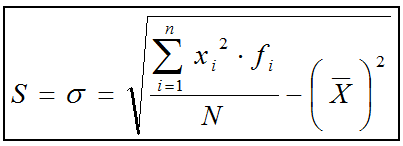
Obviamente, cuanto mayor sea la desviación típica, mayor será la
dispersión de los valores de la distribución respecto a la media
aritmética y, por tanto, bajará el nivel de representatividad de ésta
con respecto a las observaciones.
Algunas propiedades de la desviación típica son las siguientes:
Puedes practicar con el cálculo de parámetros de dispersión en ejercicios que tú mismo puedes plantear en el epígrafe sexto: "6. Manejo de Calculadora".
Algunas propiedades de la desviación típica son las siguientes:
- La desviación típica siempre es mayor o igual que cero.
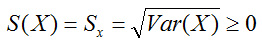
- La desviación típica no varía si a todos los datos le sumamos o restamos la misma cantidad
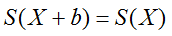
- Si multiplicamos todos los datos de la distribución por una cantidad,
la desviación típica también queda multiplicada por dicha cantidad
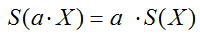
- Las dos propiedades anteriores se suelen resumir en:
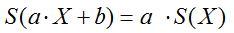
- En general, la desviación típica está menos influida por las fluctuaciones de los datos que las demás medidas de dispersión.
En la siguiente escena puedes practicar con el cálculo de la desviación típica de variables discretas y continuas
Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)
Puedes practicar con el cálculo de parámetros de dispersión en ejercicios que tú mismo puedes plantear en el epígrafe sexto: "6. Manejo de Calculadora".