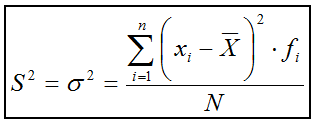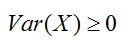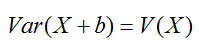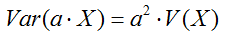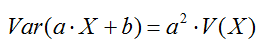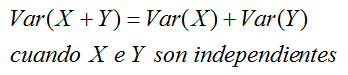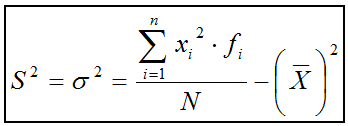La medida de dispersión más popularizada es sin duda la varianza. La filosofía de esta medida es la misma que la de la desviación media; esto es, detectar las variaciones de cada valor respecto a la media aritmética. Sin embargo para ello en lugar de utilizar el valor absoluto, eleva esas diferencias al cuadrado, con ello evita posibles compensaciones, dado que todos los términos son positivos, y además amplifica estas diferencias al elevarlas al cuadrado. Desde el punto de vista del pragmatismo matemático, es mucho más simple elevar al cuadrado que considerar el valor absoluto. Por último, considera el promedio de dichas diferencias al que denomina varianza.

Del mismo modo que ocurre para la media, la varianzaa es un parámetro muy sensible a las puntuaciones extremas. Ademas, las unidades en que se mide no son las mismas que las de los datos de la distribución.
Comparando con el mismo tipo de datos, una varianza elevada significa que los datos están más dispersos. Mientras que un valor de la varianza bajo indica que los valores están por lo general más próximos a la media.
Un valor de la varianza igual a cero implicaría que todos los valores son iguales, y por lo tanto también coinciden con la media aritmética.



Algunas propiedades de la varianza:

• La varianza es un valor siempre positivo.
  
  
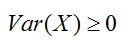
• Si a todos los datos se les suma una constante, la varianza de esos datos sigue siendo la misma.
  
  
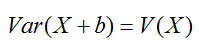
• Si todos los datos se multiplican por una constante, la varianza queda multiplicada por el cuadrado de la constante.
  
  
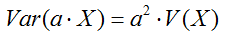
• Las dos propiedades anteriores suelen resumirse de la siguiente forma:
  
  
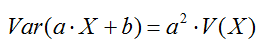
• Si se disponen de dos variables independientes
  
  

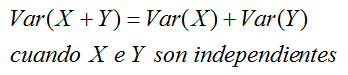
A partir de la definición de la varianza si se desarrolla la expresión y simplificando los resultados se obtiene otra expresión para la varianza que permite un cálculo más directo y sencillo.

Suele recordarse diciendo:

En la siguiente escena puedes practicar calculando la varianza de distintas series de datos, tanto para variable discreta como continua.

Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)