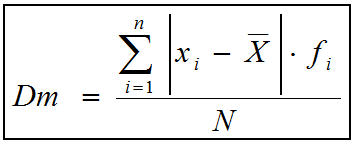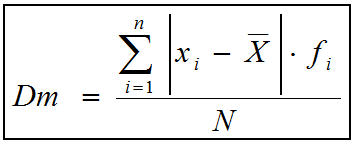En muchos procesos de fabricación se requiere mucha precisión en las medidas de determinadas piezas. Es extremadamente difícil conseguir medidas exactas puesto que toda máquina construida por el hombre es susceptible del error, no existe la máquina de precisión perfecta. Sin embargo a pesar de estas mínimas diferencias hay algunas piezas que deben rechazarse puesto que no cumplen con los criterios de medición que establecen. ¿Hasta qué punto las diferencias observadas son admisibles, pues no ocasionan ningún tipo de problema en el engranaje de dichas piezas? En estos criterios aparecen involucradas las medidas de dispersión, y entre ellas el rango y la desviación media.

Llamamos rango o recorrido, a la diferencia entre el mayor y el menor valor de la variable, indica la longitud del intervalo en el que se hallan todos los datos de la distribución. El rango es una medida de dispersión importante aunque insuficiente para valorar convenientemente la homogeneidad de los datos, de ahí que deba complementarse con otras medidas. En este sentido encontramos la variación media que nos sirve para calcular cuánto se desvían en promedio los datos de la media aritmética. Se define como la media de los valores absolutos de las diferencias entre la media aritmética y los diferentes datos.
No es una de las medidas de dispersión más usuales.



En la siguiente escena puedes practicar con el cálculo del rango y la desviación media de variable tanto discreta como continua.