Este tipo de diagramas lo han popularizado mucho los distintos
paquetes estadísticos que circulan por el universo informático y
algunas calculadores científicas que en su modo de estadística son
capaces de generarlos. Se trata de un dibujo muy sencillo que refleja
también de forma muy simple muchas de las características de la
distribución.
Se construyen fundamentalmente a partir de la información que ofrecen
la mediana y los cuartiles primero y tercero. Son los denominados
diagramas de caja y bigotes. Para la
construcción del rectángulo, la caja, solamente necesitamos las cotas que serán
los valores de Q
1 y Q
3
y para la longitud de los bigotes los valores mínimo y máximo de la
distribución. Los segmentos se dibujaran de forma continua o no
dependiendo de la presencia de lo que se denominarán valores atípicos.
En la siguiente escena podemos ver en detalle cómo se construye este tipo de diagramas.
Ahora puedes practicar y comprobar si has comprendido el significado y los elementos de los diagramas de cajas y bigotes.
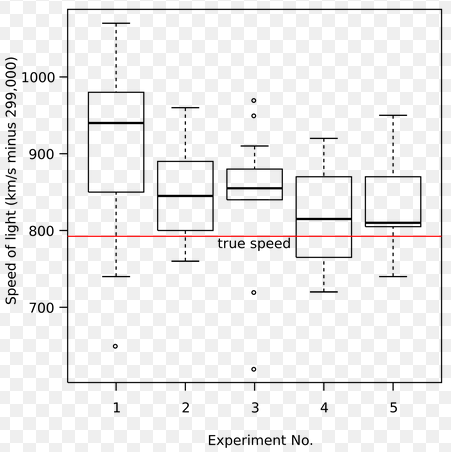
La representación gráfica de los datos
de una distribución estadística mediante los box-whisker se ha
popularizado mucho y ofrece una primera visión gráfica muy acertada de
las características principales de los elementos de la distribución.
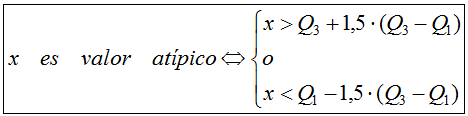
El diagrama de cajas y bigotes nos proporciona información de cómo se
encuentran concentrados los datos. Sin embargo para saber si hay algún
valor más alejado o
atípico que pueda influir distorsionando el estudio
de los diferentes parámetros estadísticos, algunos autores consideran
el siguiente criterio para distinguir y localizar a dichos posibles
valores atípicos.
Cuando existen estos valores, el convenio que existe es dibujarlos en
el box-whisker como puntos aislados en lugar de unirlos de forma
continua mediante un segmento.