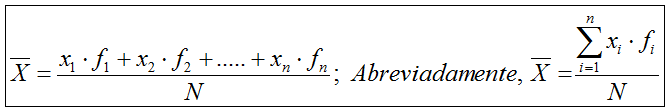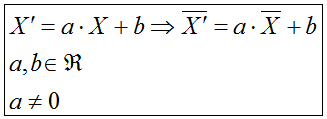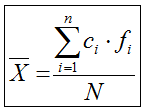De la propia definición de media
aritmética se desprenden algunas características y comentarios a cerca
de este parámetro, como por ejemplo:
- El sumatorio de las restas de cada término respecto de la media es igual a cero.
- Si todos los datos de una distribución son iguales, la media aritmética coincide con dicho dato.
La media no tiene porqué ser un valor propio de la variable.
- Es muy sensible a cambios y valores extremos en los datos.
- Se comporta de forma natural en relación a las operaciones
aritméticas suma y producto por un escalar; es decir si a todos los
datos de una distribución se les suma una misma cantidad, la media
resultante sería la anterior más dicha cantidad. Si multiplicamos
(dividimos) todos los datos de una distribución por una cantidad
distinta de cero, la media resultante sería la anterior multiplicada
(dividida) por dicha cantidad. En resumen:
Para el caso de variable continua, solamente tenemos que sustituir xi por ci
,siendo ésta última la marca de clase de cada intervalo; es decir, el
punto medio o valor central de cada intervalo. Por abuso de lenguaje se
suele utilizar indistintamente también para variables continuas el
símbolo xi para las marcas de clase
En la siguiente escena puedes practicar con el cálculo de la media para variable discreta.
Y en la siguiente escena puedes ver ejemplos para el cálculo de la media para variable discreta y continua.
Y en la siguiente puedes ver más ejemplos.
Escena desarrollada por José Ireno Fernández Rubio, María José García Cebrian y Consolación Ruiz Gil
(RED Descartes)
Para completar el estudio sobre la media también puedes consultar más información sobre la
Media ponderada pulsando sobre la imagen siguiente:
y sobre la
Media geométrica y la
Media armónica pulsando sobre esta otra imagen: