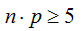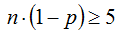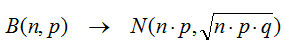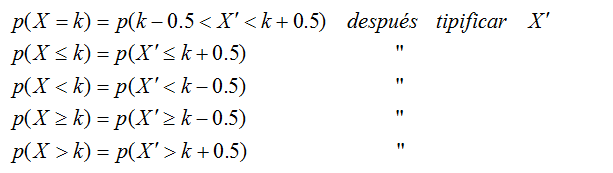5. Teorema de Moivre.

Este resultado establece las condiciones en las que una distribución discreta como la binomial puede aproximarse por una distribución normal, proporcionando además los parámetros media o esperanza y desviación típica de dicha distribución normal.

La sencillez de las condiciones que establece el teorema, el ahorro operacional que proporciona  y la calidad de la aproximación hace que sea uno de los resultados más utilizados en estadística.

Supongamos una distribución binomial B( n , p ) en la que se cumplan simultáneamente las condiciones:

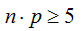
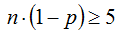
Entonces:

En la siguiente escena puedes practicar un poco con las condiciones y tesis del teorema de Moivre. Si pulsas el botón de dibujar la normal, observarás la poca diferencia que ofrece la aproximación.

Escena de Juan Jesús Cañas Escamilla(RED Descartes)

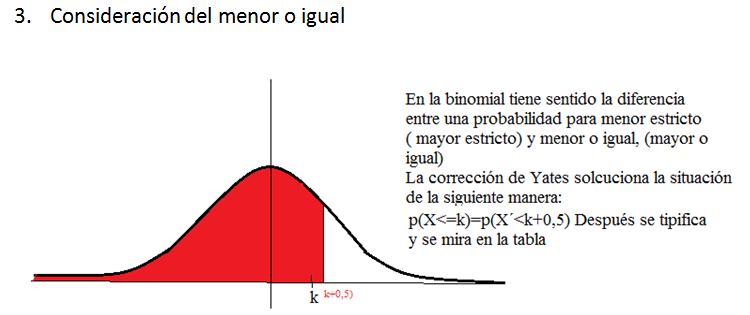
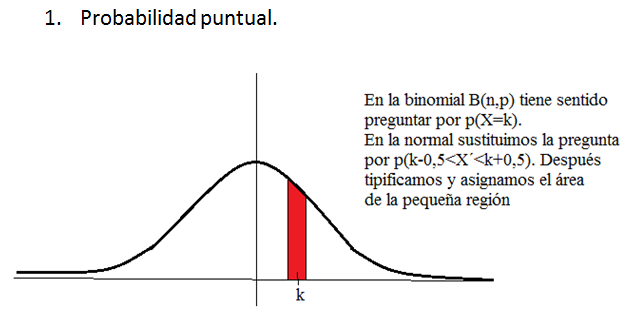
CORRECCIÓN POR CONTINUIDAD (Corrección de Yates):
La distribución binomial es una variable discreta y por tanto tiene sentido el preguntarnos tanto por probabilidades puntuales,  como por probabilidades en las que sí tenga importancia saber si el primer o último valor entra o no entra en las posibilidades del problema. Sin embargo, cuando efectuamos la aproximación por una distribución normal, por tanto continua, las consideraciones anteriores dejan de ser determinantes, ya que la primera no tendría sentido y la segunda no ofrecería diferencia alguna.
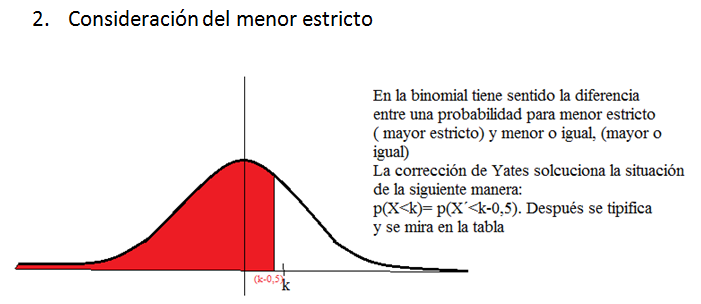
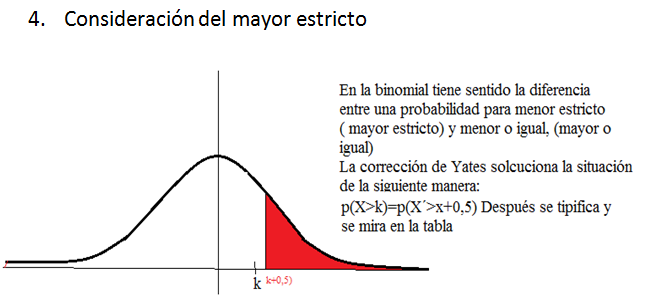
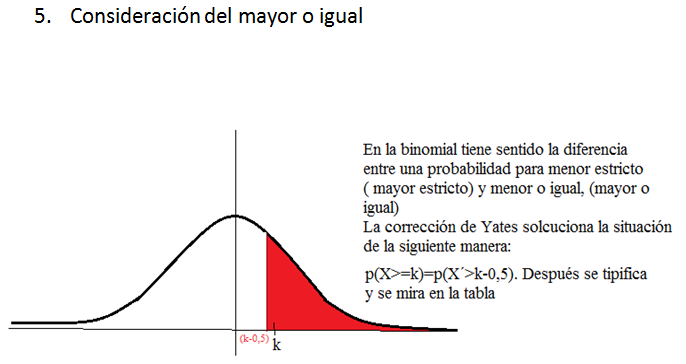
Para aclarar y diferenciar este tipo de situaciones se ha adoptado como norma general realizar correcciones que vienen a solucionar ese matiz diferenciador en las distribuciones discretas, que se “difumina” en la aproximación mediante una distribución continua. En este sentido convenimos efectuar las siguientes"correcciones" sobre los valores, conocidad popularmente como correciones de Yates

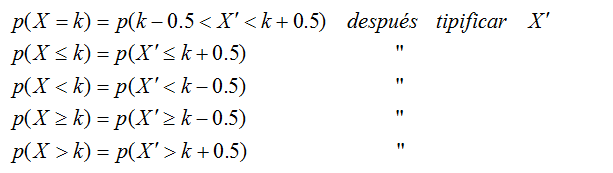
Veamos un ejemplo muy sencillo de aplicación del teorema de Moivre con la corrección de Yates.

Supongamos que el 90% de los miembros de un club pasan sus vacaciones en la playa. Calcula una aproximación, obtenida utilizando tablas de la normal, de la probabilidad de que, en un grupo de 6000 miembros del club, 5450 o menos vayan a ir a la playa a pasar sus vacaciones.