Se trata de calcular el valor de la distribución
N(0,1) que llamaremos
za
y que proporciona una probabilidad a la derecha o barrido a la
derecha de valor "k", es decir tal que p( z > z
a )= k. Teniendo en cuenta que en la tabla de la
N(0,1)
los valores que aparecen corresponden a barridos a la izquierda,
debemos realizar una táctica sencilla que permita localizar el valor z
a .
- Si a la derecha deja una probabilidad de valor "k", eso
significa que a la izquierda dejará un valor de "1-k". por tanto
p( z < za )=1- k .
-
Normalmente el valor de "1-k" no coincidirá exactamente con uno de los
que aparece en la tabla, por tanto debemos considerar el más proximo.
En el caso en el que haya dos o más que estén a la misma distancia de
"1-k", lo habitual es considerar como valor de za la media aritmética de los calculados.
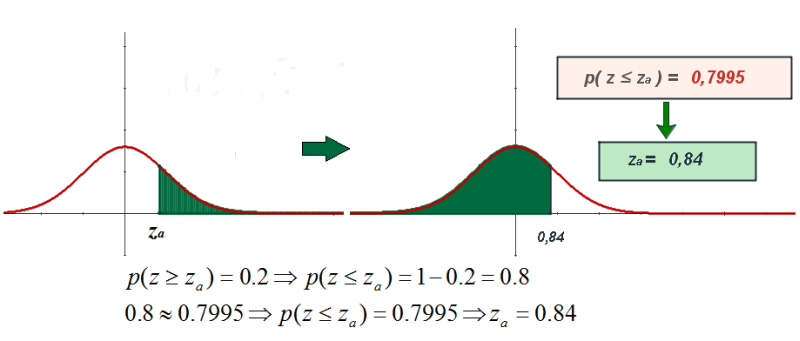
Por ejemplo, supongamos que nos interesa conocer el valor de la distribución
N(0,1) tal que la probabilidad a la derecha de ese valor sea de 0.2. es decir el valor z
a tal que p( z > z
a ) = 0.2.
- Si p( z > za ) = 0.2, entonces p( z < za ) = 1- es decir p( z < za ) = 0.80.
- El valor no coincide con ningún valor de la tabla, por tanto considero el más próximo. En este caso 0.7995.
- Extrapolamos el valor para localizar el za . En este caso za = 0.84
En la siguiente escena puedes calcular
directamente y sin necesidad de utilizar ninguna tabla los valores que
dejan una probabilidad a la derecha de lo que quieras. Basta con que
introduzcas el valor deseado en el control
<<probabilidad>>. No obstante puedes practicar el cálculo
de este tipo de valores con la tabla de la N(0,1)
. también puedes utilizar la escena para comprobar el error que se
comete al realizar los cálculos de forma manual, (con la tabla) o de
forma directa en la escena.