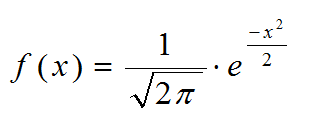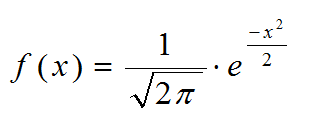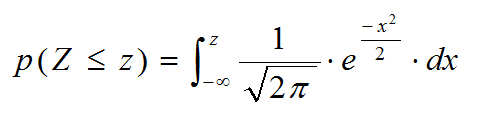2.1. La distribución normal cero uno

Entre la familia de las distribuciones normales, la que tienen por media cero y por desviación típica uno es sin duda la más importante de todas. Esta distribución aparece totalmente tabulada y como veremos más adelante permitirá el cálculo de cualquier tipo de probabilidad en cualquier tipo de distribución normal.
La notación que emplearemos para referirnos a esta normal será N(0,1).
Su función de densidad viene dada por la fórmula:

Como ya se ha mencionado al principio del tema, el cálculo de probabilidades en variable continua se asocia al cálculo de áreas. En el caso particular de la distribución N(0,1)
si queremos calcular el valor de que la variable tome un valor menor o menor o igual que "z", tendríamos que calcular un área mediante el proceso de integración indefinida, con la dificultad añadida de que la función a integrar no admite una primitiva en términos de función elemental.

Afortunadamente no tendremos que realizar este tipo de ejercicio cada vez que queramos calcular una probabilidad ya que disponemos de una tabulación que permite calcular con bastante precisión el valor de que la variable tome valores menores o menores o iguales que cualquier valor "z" comprendido entre 0 y 4 con incrementos de una céntésima.
Esto será suficiente para localizar cualquier tipo de probabilidad como veremos más adelante.

Escena de Juan Jesús Cañas Escamilla(RED Descartes)

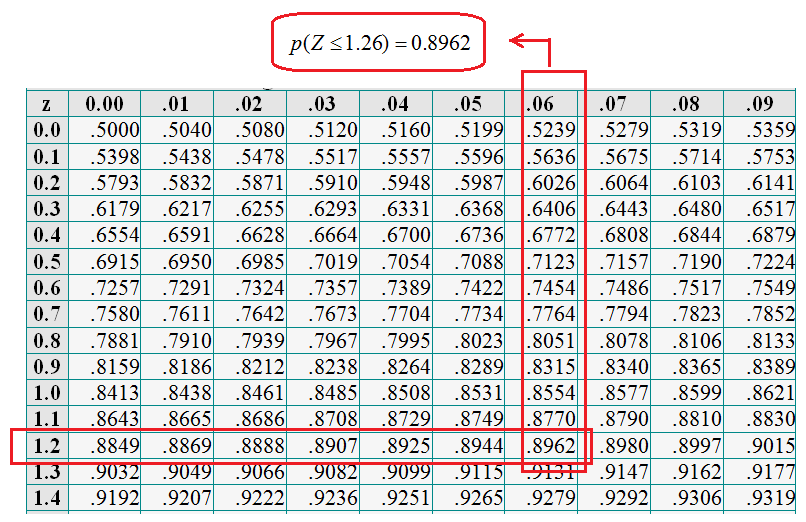
Detalle de la tabulación de la N(0,1). Ejemplo de cáculo de una probabilidad (aréa correspondiente al barrido a la izquierda de la función)