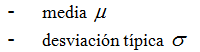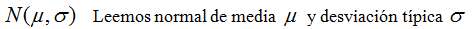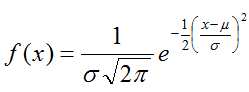2. La distribución normal
La distribución normal es sin duda la
más importante de las distribuciones continuas tanto en la teoría como
en la práctica estadística. Puede decirse que en este universo, la
mayoría de los fenómenos naturales se comporta básicamente de forma
normal o“gaussiana”. En estadística inferencial, el teorema central del
límite y las pruebas de normalidad sobre una serie de datos, van a ser
básicas en el desarrollo moderno de la estadística.
Aunque fue reconocida por primera vez por el francés Abraham de
Moivre (1667-1754), posteriormente, Carl Friedrich Gauss
(1777-1855) elaboró desarrollos más profundos y formuló la ecuación de
la curva. Se suele conocer popularmente como la "campana de Gauss".
La distribución de una variable normal está completamente determinada por el conocimiento de dos parámetros:
La notación que emplearemos será:
La expresión de la función de densidad para la distribución normal viene dada por:
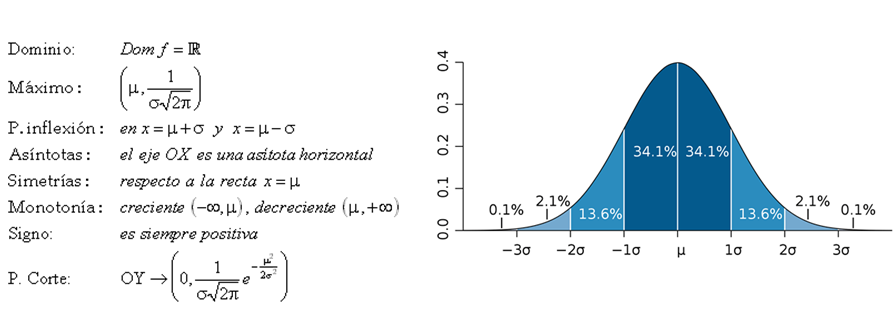
Las principales características (propiedades) de esta función son:
En la siguiente escena puedes manipular
los controles para observar el comportamiento de la gráfica de la
distribución normal cuando cambias la media y la desviación típica de
la misma.
Puedes observar dos clases sobre la distribución normal correspondientes a la Universidad Politécnica de Valencia.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
Vídeo enlazado desde YouTube, licencia de YouTube estándar