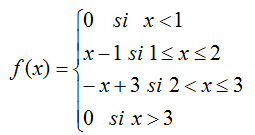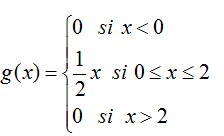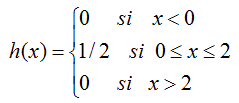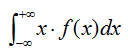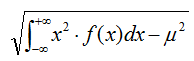1. Introducción.

Las distribuciones de probabilidad de una variable aleatoria continua pueden imaginarse como idealizaciones del polígono de frecuencias, asociado al histograma de frecuencias relativas, cuando se aumenta indefinidamente el número de datos y se disminuye paulatinamente la amplitud de los intervalos. Este proceso “límite” proporciona una primera idea de función asociada a dicha variable continua.
Las distribuciones de probabilidad de una variable continua se definen a partir de una función particular a la que llamaremos función de densidad.
Consideremos inicialmente un ejemplo:
En un instituto se decide estudiar el tiempo, llamémosle X, que emplean los alumnos en desplazarse desde su casa hasta él. Se trata de una variable estadística que al menos teóricamente puede tomar cualquier valor dentro de un determinado intervalo (entre 0 y 20 minutos por ejemplo).
Este tipo de variable se suele representar gráficamente mediante un histograma que consiste en levantar un rectángulo sobre cada uno de los intervalos (clases) donde toma sus valores. La base del rectángulo es la amplitud del intervalo. Si variamos las bases de los intervalos, evidentemente cambia la forma del histograma.
Si el número de alumnos a los que controlamos el tiempo fuese suficientemente grande y vamos aumentando el número de intervalos (o lo que es lo mismo, consideramos clases cada vez más pequeñas), la línea poligonal que forman los puntos medios de los lados superiores de los rectángulos, llamada poligonal de frecuencias tiende a una curva que recibe el nombre de Función de Densidad de la variable X.

En la siguiente escena puedes observar el proceso límite que vislumbra la idea de función de densidad. Por motivos de agilidad en cuanto al funcionamiento de la escena se considera un máximo de 100000 en el control correspondiente a población y un máximo de 50 en el control de partición, (límite de intervalos que se consideran).

Escena de Juan Jesús Cañas Escamilla(RED Descartes)

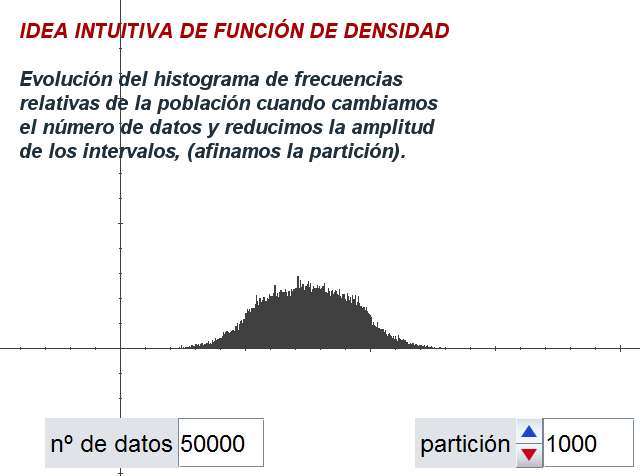
En la siguiente imagen puedes observar el resultado que ofrece la escena anterior para el caso de una población de 50000 elementos y una partición de 1000 intervalos

Una función f(x) se admite como función de densidad de una variable aleatoria continua X si verifica:

• La función f(x) es positiva o nula en todo el dominio de definición
• El área limitada por la gráfica de la función y el eje de abscisas (OX) es igual a la unidad.
  
  

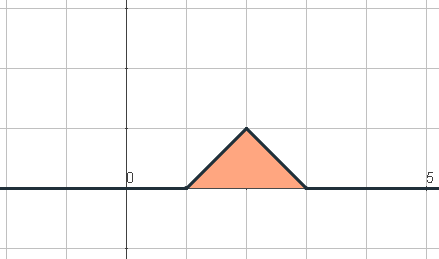
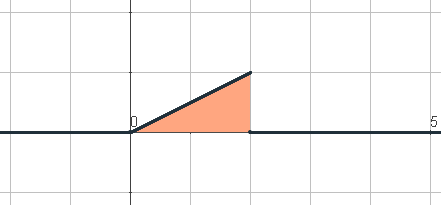
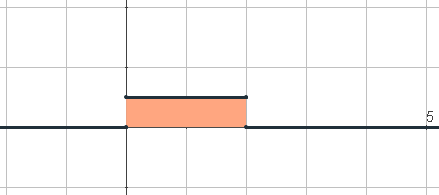
Algunos ejemplos de función de densidad

Nota:
En variable continua no tiene sentido el estudio de la probabilidad en un valor aislado (siempre sería cero), pero sí lo tiene el de considerar la probabilidad de que la variable tome valores comprendidos dentro de un intervalo.
Asociaremos la probabilidad de que una variable continua tome valores entre los puntos del intervalo [a , b] como el área comprendida entre la curva, el eje OX y las rectas
x = a  y  x = b.
Los parámetros asociados a una variable continua tienen una forma de calcularse que excedería de los contenidos de un curso de bachillerato.
La media o esperanza matemática es el valor más representativo de todos los que toma la variable continua X, puede imaginarse como el punto sobre el eje de abscisas en el cuál la superficie generada por la función y el eje permanecerían en equilibrio. El cálculo matemático se haría:

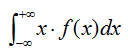
La desviación típica se define como una medida de la dispersión de los valores de la variable X con respecto a la media. Mientras más pequeña sea la desviación más estrecha será la gráfica de f(x) respecto a la media. Su cálculo se haría: