- Formulación de la hipótesis nula y de la hipótesis alternativa. Como norma general, se debe tener en cuenta que aquello que queramos demostrar debe ir siempre a la hipótesis alternativa.
Por otra parte si lo que queremos demostrar está en la hipótesis
alternativa, el error de equivocarnos lo tendremos medido ya que sería
el nivel de significación.
-
Planteamiento de hipótesis de contraste para el caso de una proporción:

- Planteamiento de hipótesis de contraste para el caso de una media:

-
Elección del estadístico de contraste ( en nuestro caso media o proporción muestral).
Algunos autores prefieren considerar intervalos de confianza o semirectas de confianza para los parámetros a contrastar e investigar, es deci, si los valores obtenidos en las muestras están o no en dichos intervalos (semirectas), pero nosotros vamos a definir unos estadísticos que simplemente proceden de la tipificación de variables en el muestreo cuyas distribuciones son perfectamente conocidas y que por tanto al tipificarse seguirán una distribución normal de media cero y desviación típica uno. Una vez calculado el valor de estos estadísticos se observará si quedan dentro o fuera de las regiones determinadas (según sea el tipo de contraste) por el nivel de significación.
-
Estadístico de contraste para el caso de una proporción.
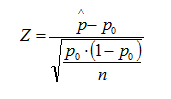
-
Estadístico de contraste para el caso de ua media con desviación típica poblacional conocida.
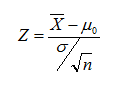
-
Estadístico de contraste para el caso de ua media con desviación típica poblacional desconocida.
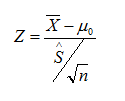
-
Determinación de la
región de rechazo.
A partir del nivel de significación previamente fijado se establece el intervalo o semirecta que constituirán la zona de aceptación y rechazo según si el estadístico de contraste esté dentro o fuera de dicha zona.
-
Región de aceptación y rechazo en un contraste bilateral.
A partir del nivel de significación y haciendo uso de la tabla de la normal cero uno, a través de la estrategia conveniente se pueden localizar los valores críticos, tal como se hizo en el tema de intervalos de confianza.
En la siguiente escena puedes practicar con la localización de la región crítica en contrastes bilaterales. La escena te lo proporciona directamente aunque te recomendamos que utilices la tabla de la normal y después compares tus resultados con los que ofrece la escena.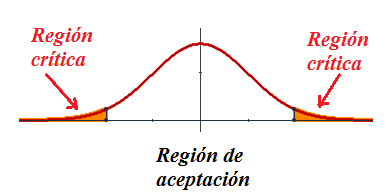
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
-
Región de aceptación y rechazo en un contraste unilateral derecho
A partir del nivel de significación y haciendo uso de la tabla de la normal cero uno, a través de la estrategia conveniente se puede localizar el valor crítico, que deja a su derecha una probabilidad igual al nivel de significación de la misma forma que se hizo en el tema de la distribución normal.
En la siguiente escena puedes practicar con la localización de la región crítica en contrastes bilaterales. La escena te lo proporciona directamente aunque te recomendamos que utilices la tabla de la normal y después compares tus resultados con los que ofrece la escena.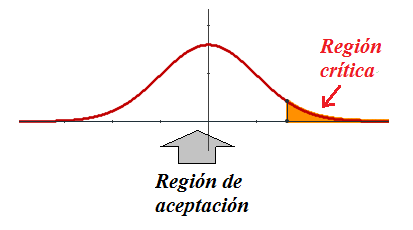
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
-
Región de aceptación y rechazo en un contraste unilateral izquierdo
A partir del nivel de significación y haciendo uso de la tabla de la normal cero uno, a través de la estrategia conveniente se puede localizar el valor crítico, que deja a su izquierda una probabilidad igual al nivel de significación de la misma forma que se hizo en el tema de la distribución normal.
En la siguiente escena puedes practicar con la localización de la región crítica en contrastes bilaterales. La escena te lo proporciona directamente aunque te recomendamos que utilices la tabla de la normal y después compares tus resultados con los que ofrece la escena.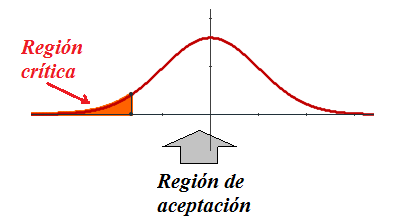
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
- Consideración de una muestra
En esta muestra elegida de forma aleatoria se calculara el valor correspondiente (en nuestro caso media muestral o proporción) y que permiten localizar el valor del estadístico de contraste
Por ejemplo si se quiere contrastar que el peso medio de las tarrinas de helado de 100 gramos no tienen realmente ese peso. En primer lugar elegimos por ejemplo una muestra aleatoria de 40 tarrinas ()para no tener problemas de normalidad) y calculamos la media muestral y la desviación típica muestral. Supongamos que la media muestral es 103,25 gramos y la desviación típìca 5,345 gramos.
El valor en este caso del estadístico de contraste sería:
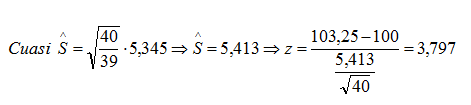
-
Aceptación o rechazo de la hipótesis nula
La aceptación o rechazo de la hipótesis nula depende de si el valor del estadístico de contraste calculado en nuestra muestra está dento o fuera de la zona de aceptación.

-
Interpretación de la decisión tomada.
Existen muchas formas de redactar las conclusiones a las que se llega cuando aceptamos o rechazamos la hipótesis nula en un contraste. Aquí sugerimos una muy sencilla.
-
Para el caso de aceptación de la hipótesis nula.
Simplemente decir que: "A partir de los datos estadísticos obtenidos en la muestra, se acepta con un nivel de significación (...) aquello que diga la hipótesis nula" o también "A partir de los datos estadísticos obtenidos en la muestra no existen evidencias estadísticamente significativas a nivel (...) que permitan afirmar o demostrar aquello que diga la hipótesis alternativa".
- Para el caso de rechazo de la hipótesis nula.
"A partir de los datos estadísticos obtenidos en la muestra existen evidencias estadísticamente significativas a nivel (...) que permiten afirmar o demostrar aquello que dice la hipótesis alternativa, con riesgo de equivocarnos igual al nivel de significación".
Resumimos todo en el siguiente ejemplo:
Un informe de la Asociación de Compañías Aéreas (ACA) indica que el precio medio del billete de avión desde la ciudad A a la ciudad B es de 120 euros. Para contrastar esta información se considera una muestra aleatoria de 100 viajeros entre estas dos ciudades que volaron en distintas compañías, en la que se observó que la media del billete era de 128 euros y una desviación típica de 40 €.
¿Se puede considerar con un nivel de significación del 1% que la información de la ACA es correcta?



