- Hace ya algunos años, (década de los ochenta), se decía que la estatura media de los jóvenes españoles de entre 20 y 21 años era de 172 cm. Los datos se extraían de las tallas que se obtenían de los entonces llamados “quintos”, jóvenes que ingresarían en el ejército para cumplir el servicio militar obligatorio. Sin embargo hoy en día, siglo XXI, se observa en cualquier muestra como en una cola de un cine, en un supermercado, en uan clase de bachillerato o en una fiesta que los jóvenes parecen significativamente más altos, con lo que deberíamos revisar el parámetro media poblacional, ya que seguramente habrá cambiado. REVISAR LA HIPÓTESIS DE QUE LA MEDIA DE LOS JÓVENES ESPAÑOLES ES DE 172 CM.
- En cierta ciudad se observó que el 70% de la población era favorable a que una determinada persona ejerciera como alcalde de la misma. Después de varios años de controvertida gestión el descontento es evidente y parece lógico revisar el porcentaje de aceptación. REVISAR LA HIPÓTESIS DE QUE LA PROPORCIÓN DE GENTE FAVORABLE AL ALCALDE SE MANTIENE EN EL 70%.
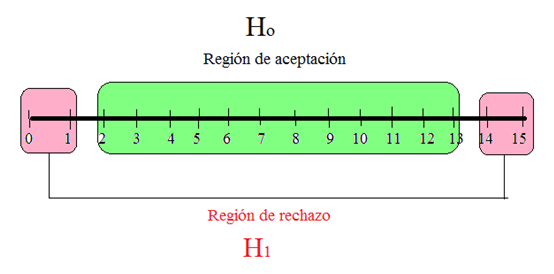
IDEA SOBRE UNA REGLA DE DECISIÓN
Cualquier persona a lo largo de su vida utiliza reglas de decisión ante situaciones concretas. Incluso esas reglas a veces son irracionales e incluso disparatadas.
- Para saber si me irá bien con la decisión tomada consulto con un adivino y su bola de cristal.
- Los generales romanos ofrecían sacrificios y consultaban con los sacerdotes y magos para saber si les iría bien en la batalla.
- Mi horóscopo dice que ahora no debo realizar ninguna inversión.
- Si encesto la bola de papel en la papelera aprobaré el examen...¡vaya!..., bueno a la tercera...
 |
 |
 |
 |
Otras veces también se recurre a procedimientos mucho más lógicos y científicos.
- Antes de realizar un viaje consultar la previsión meteorológica.
- Si hago bien las preguntas de autoevaluación del libro, posiblemente haré bien las del examen.
En estadística para decidir sobre dos situaciones competitivas, complementarias y excluyentes recurriremos al procedimiento conocido por el nombre de Contraste de Hipótesis.