Analizando un poco el problema, en realidad no importa el orden en que aparezcan los pastelitos en mi bandeja. Observamos también que pueden repetirse pasteles, incluso se podría comprar una bandeja de seis dulces iguales. Estamos por tanto ante una combinación, (no importa el orden) y con posibilidad de repetición. Estamos ante una combinación con repetición de 20 elementos tomados de 6 en 6. CR,20,6.

Denominamos combinaciones con repetición de n elementos tomados de m en m, (ninguna limitación con respecto a n y m), a las distintas agrupaciones de m elementos elegidos de entre los n de manera que:
El número de combinaciones ordinarias de m elementos tomados de m en m ,lo denotaremos CRn,m y se calcula:
- En cada grupo entren m elementos repetidos o no
- Dos grupos son distintos si difieren en algún elemento.
El número de combinaciones ordinarias de m elementos tomados de m en m ,lo denotaremos CRn,m y se calcula:
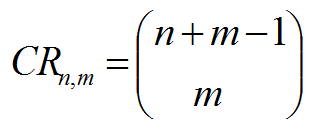
Para explicar la fórmula anterior
vamos a desarrollar un método de codificación que nos ayude sobre un
ejemplo concreto y que sea un poco más fácil que el de al principio.
Supongamos que en un restaurante se ofrecen cuatro posibilidades de menús; digamos A, B, C y D. Si un grupo de 6 amigos decide hacer un pedido, calculemos todos los casos distintos que podrían realizarse. Desde el punto de vista combinatorio, estamos ante combinaciones con repetición de cuatro elementos tomados de seis en seis.
En primer lugar utilizamos tres líneas (rayas) para separar las cuatro posibles opciones de los distintos menús. También utilizaremos el símbolo(.) (punto) para significar el pedido de cada persona. De esta forma, el pedido de por ejemplo cuatro menús A y dos menús B lo codificaríamos:
Supongamos que en un restaurante se ofrecen cuatro posibilidades de menús; digamos A, B, C y D. Si un grupo de 6 amigos decide hacer un pedido, calculemos todos los casos distintos que podrían realizarse. Desde el punto de vista combinatorio, estamos ante combinaciones con repetición de cuatro elementos tomados de seis en seis.
En primer lugar utilizamos tres líneas (rayas) para separar las cuatro posibles opciones de los distintos menús. También utilizaremos el símbolo(.) (punto) para significar el pedido de cada persona. De esta forma, el pedido de por ejemplo cuatro menús A y dos menús B lo codificaríamos:
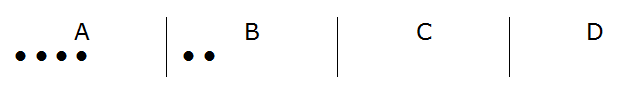
Es
decir el código del pedido sería:


Si por ejemplo quisiéramos codificar el pedido de seis menús D su codificación sería la siguiente:
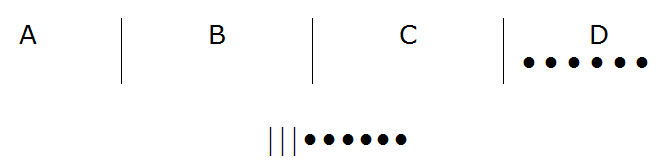
La posición inversa también se manifiesta asequible, es
decir, descifrar cualquier código que se confeccione con tres rayas y
seis puntos como un determinado y único pedido también sería sencillo.
Por ejemplo si queremos descifrar el código ..|..||..
,lo podríamos interpretar como dos menús A, dos menús B, ningún menú C
y dos menús D. Veamos algún ejemplo más de codificación:

Se ha establecido por tanto una
correspondencia biunívoca entre las combinaciones con repetición de
cuatro elementos tomados de seis en seis y las distintas agrupaciones
de seis puntos y tres rayas; esto es, las permutaciones con repetición
de 9 elementos donde uno se repite tres veces y otro seis. A su vez
cada agrupación de dichos los seis puntos se pueden ir situando en las
distintas posiciones siendo indiferente el orden (ya que los puntos son
indistinguibles), podría ser considerada como una combinación de 9
elementos tomados de 6 en 6.
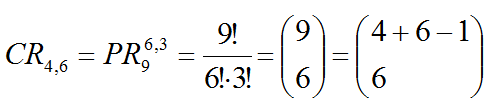
En la siguiente escena puedes practicar con ejemplos de formación de algunas combinaciones con repetición.
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)