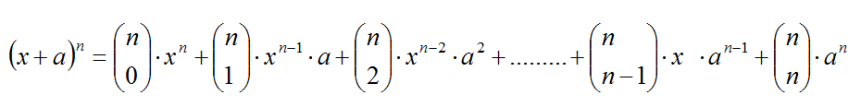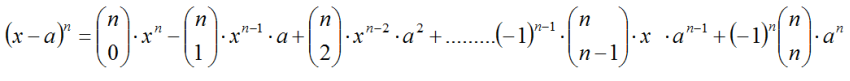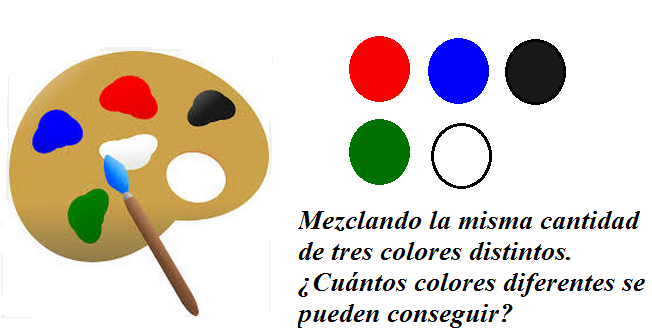
Así pues, todas las permutaciones de estos tres colores se deberían analizar como una sola agrupación. Por tanto, para localizar todos los posibles colores resultantes de la mezcla de tres de los cinco de que disponemos, V5,3 entre las P3 .
A este tipo de agrupación la denominaremos Combinación sin repetición.
Existen otras muchas situaciones parecidas en las que necesitamos conocer el número de agrupaciones en las que NO IMPORTA EL ORDEN. Por ejemplo:
- Seleccionar cuatro alumnos de una clase que irán de excursión
- Repartir cinco entradas entre diez amigos para ir a un concierto.
- Juego de la lotería primitiva
Denominamos combinaciones ordinarias o sin repetición de n elementos tomados de m en m, (siendo m menor o igual que n) a las distintas agrupaciones de m elementos de manera que:
- En cada grupo entren m elementos distintos
- Dos grupos son distintos si difieren en algún elemento.
El número de combinaciones ordinarias de m elementos tomados de m en m ,lo denotaremos Cn,m y se calcula:
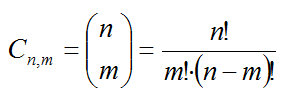
Se puede observar fácilmente que: Las combinaciones sin repetición de n elementos tomados de m en m, podrían formarse a partir de considerar las variaciones sin repetición de n elementos tomados de m en m y posteriormente identificar las posibles reordenaciones de una agrupación, (permutaciones de m elementos), como una única ya que el orden no interviene en la agrupación que estamos considerando; esto es:
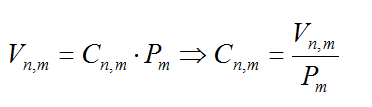
En el siguiente video podemos observar el planteamiento de un problema que requiere de la combinatoria y su solución.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
En la siguiente escena puedes practicar con ejemplos de formación de algunas combinaciones sin repetición.
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
7.1. Propiedades de los números combinatorios
Los números combinatorios aparecen
muy frecuentemente en multitud de situaciones en Matemáticas, Física,
Biología, etc...Figuran como tecla directa en cualquier calculadora
científica. Como propiedades más interesantes merecen destacarse:
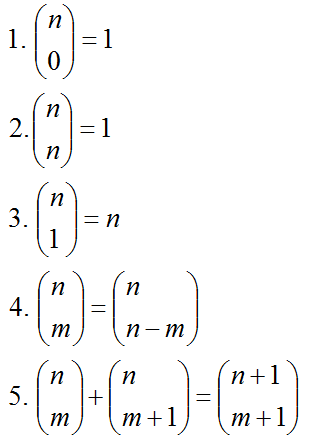
Cuando no existían calculadoras
científicas, el cálculo de números combinatorios requería de un trabajo
complicado. El triángulo de Pascal permitía de una forma recurrente y
muy fácil calcular cualquier número combinatorio, aunque es verdad que
para cantidades elevadas también era bastante engorroso.
En el siguiente video se realiza un análisis del triángulo de Pascal.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
En la siguiente escena puedes ver muchas líneas del triángulo de Pascal y unas propiedades curiosas.
Escena desarrollada por Miguel Ángel Cabezón Ochoa(RED Descartes)
7.2. Binomio de Newton
Una de las aplicaciones más interesantes
desde el punto de vista algebraico para los matemáticos, constituye el
desarrollo de las distintas potencias de un binomio. Conocido
como binomio de Newton, utiliza los números combinatorios y sus
propiedades para desarrollar de forma fácil y directa la potencia
natural de cualquier expresión del tipo: